General Field Relations for Time Varying Electric and Magnetic Fields

General Field Relations for Time Varying Electric and Magnetic Fields

• In general, the electric charge possesses a basic important property that it can not be created nor distroyed. In other words if the charge disappears from one point, then it must reappear at some other point. This basic property is called conservation of charge.

1. Equation of Continuity for Time Varying Fields

• The basic relation between an electric and magnetic field, starting from Faraday's law is given by,

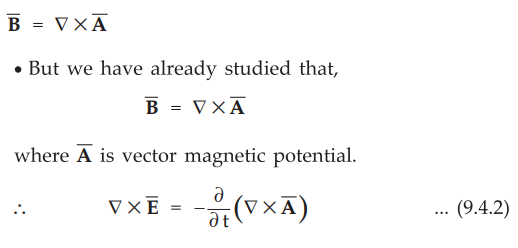
• Intercharging operators at R.H.S. of above equation, we get,

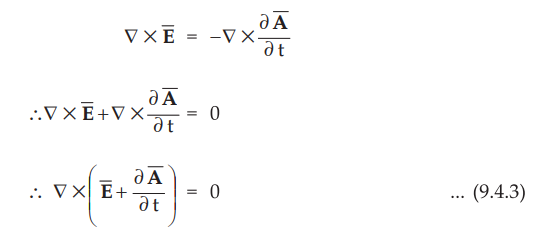
• But according to vector identity 'curl' of a gradient of a scalar is always zero. Hence we can write,

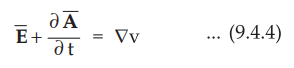
• As R.H.S. of the equation (9.4.3) including curl is zero, we can introduce negative sign at R.H.S. of the equation (9.4.4).

• Consider any closed surface. If the current is flowing out of the surface, we can write

I = dQ / dt A i.e. C/sec

• As current is flowing out of the surface, it indicates that positive charge is going out. So the positive charge is decreasing internally. Let Q_I be the internal charge,

I = - dQ_I / dt .... (9.4.7)

• If there is a volume charge ρv, then we can write,

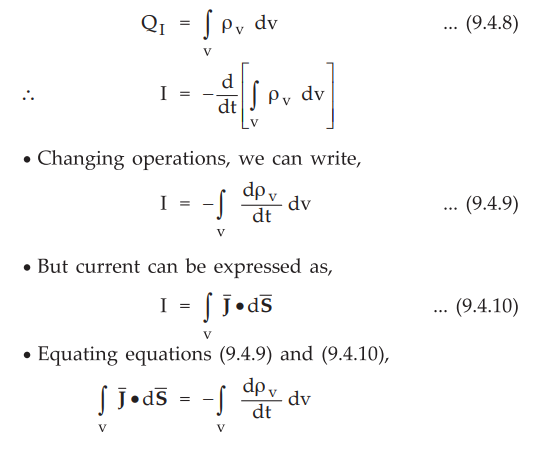
• Using divergence theorem, converting surface integral to volume integral, assuming that the volume V is enclosed by the same surface S.

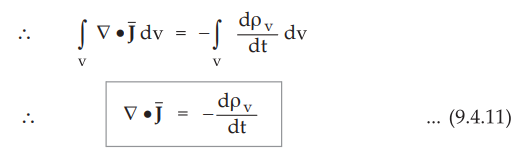
• Equation (9.4.11) is called equation of continuity of current in point or differential form.

2. Inconsistency of Ampere's Circuit Law-Modification in Equation of Continuity

• Consider Ampere's circuit law in point or differential form as,

• Taking divergence on both sides of above equation, we get,

• According to vector identity, 'divergence of curl' of vector is zero.

• But 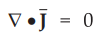 is valid only for static fields. This result is not consistent with the continuity equation 

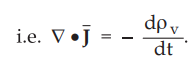
In otherwords, Ampere’s circuit

law is not consistent and needs some modification. Let us consider some unknown term . Then we can modify Ampere's circuit law for time varying fields as,

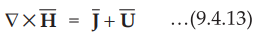
• Taking divergence on both the sides, we get,

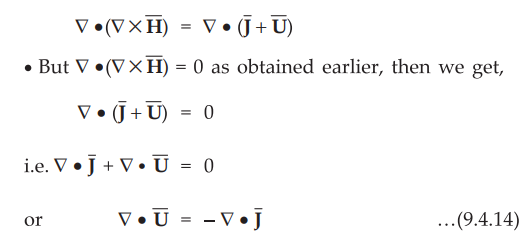
• But from the continuity equation for time varying fields,

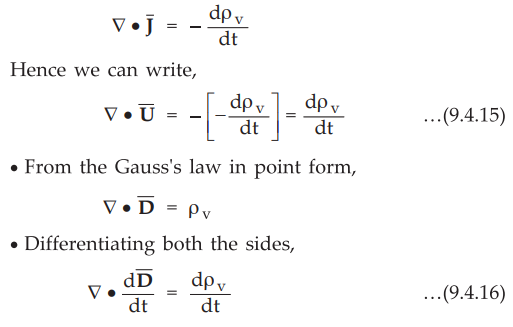
• Hence the expression for unknown term can be obtained as,

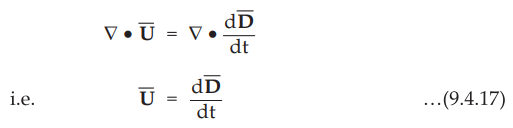
• Hence for time varying field, Ampere's circuit law can be written as,

 Review Questions

1. What is displacement current ? How is Maxwell's equation modified to account for it in time varying field ?

2. State and derive equation for continuity under dynamic field conditions. Derive point form of equation of continuity for time varying fields.

3. Explain inconsistency of Ampere's law. How it is overcome by modifying equation of continuity ?