Probability and complex function: Unit V: Ordinary Differential Equations
Higher order linear differential equations with constant coefficients
(a) General form of a linear differential equation of the nth order with constant coefficients is, (b) (i) The general form of the linear differential equation of second order is d2y / dx2 + P dy/ dx + Qy = R.
HIGHER ORDER LINEAR DIFFERENTIAL EQUATIONS WITH CONSTANT
COEFFICIENTS.
(a) General form of a linear differential equation of the nth order with constant coefficients is
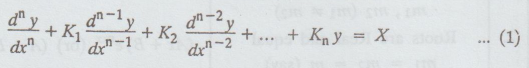
where
K1, K2, .... Kn are constants.
Such
equations are most important in the study of electro-mechanical vibrations and
other engineering problems.
In
discussing linear equations with constant coefficients, it will be convenient to
denote the operation d / dx by a single letter D. Thus, D is the differential operator, so that
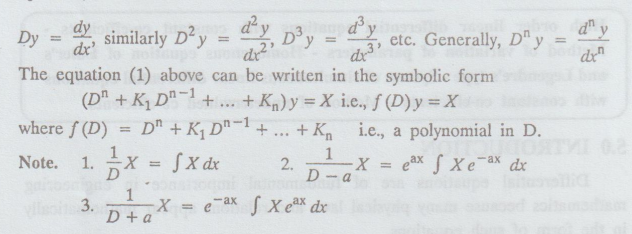
(b) (i) The general form of the linear differential equation of second order is
d2y
/ dx2 + P dy/ dx + Qy = R.
where
P and Q are constants and R is a function of x or constant.
(ii)
Differential operators
The
symbol D stands for the operation of differential
(i.e.,)
Dy = dy/ dx , D2 y = d2y / dx2 , 1/ D stands for the operation of integration.
1/
D2 stands for the operation of integration twice.
d2y
/ dx2 + P dy / dx + Qy = R
can be written in the operator form
D2y
+ PDy + Qy = R (or) (D2 + PD + Q) y = R
(iii)
Complete solution is y = Complementary function + Particular Integral
(iv)
To find the Complementary functions

(v) To find the particular integral :

Result :
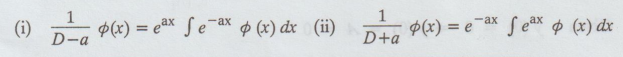
Probability and complex function: Unit V: Ordinary Differential Equations : Tag: : - Higher order linear differential equations with constant coefficients
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
