Probability and complex function: Unit V: Ordinary Differential Equations
Homogeneous equation of euler's and legendre's type
Ordinary Differential Equations
The general form of "linear equation of second order" is given by d2y/dx2 + P dy/dx + Qy = R
HOMOGENEOUS EQUATION OF EULER'S AND LEGENDRE'S
TYPE
The
general form of "linear equation of second order" is given by
d2y/dx2
+ P dy/dx + Qy = R
where
P, Q and R are functions of x only.
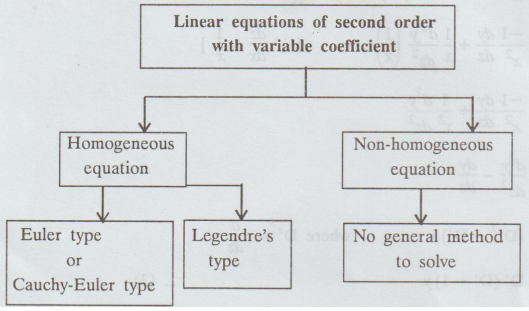
Homogeneous equations of Euler type:[Cauchy's type]
Linear
Differential Equations with Variable Co-efficients
An
equation of the form
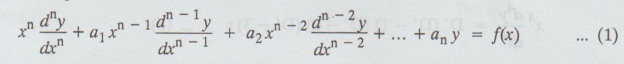
where
a1, a2,....an are constants and f(x) is a
function of x. 2 Equation (1) can be reduced to linear differential equation
with constant co-efficients by putting the substitution.
x = ez (or) z = log x.

and
so on. Substituting (2), (3), (4), (5) and so on in (1), we get a differential
equation with constant coefficients and can be solved by any one of the known
methods.
Note :
The logarithm to the base e is known as the natural logarithm or the Napierian logarithm, after Napier, the inventor of logarithms.
In theoretical work, we use natural logarithms and so the suffix e is generally omitted, the base e being understood.
Probability and complex function: Unit V: Ordinary Differential Equations : Tag: : Ordinary Differential Equations - Homogeneous equation of euler's and legendre's type
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
