Implementation of Logic Functions using Logic Gates

Implementation of Logic Functions using Logic Gates

 

1. Summary of Logic Gates

• Logic gates are the basic elements that make up a digital system. The electronic gate is a circuit that is able to operate on a number of binary inputs in order to perform a particular logical function. The types of gates available are the NOT, AND, OR, NAND, NOR, exclusive-OR, and the exclusive-NOR.

Note : EX-OR and EX-NOR gates are also known as mutually exclusive gates.

 

2. Universal Gates

• The NAND and NOR gates are known as universal gates, since any logic function can be implemented using NAND or NOR gates.

• The simplified Boolean expression can be implemented using basic gates. When we implement logic circuit using basic gates, we require ICs for AND, OR and NOT gates. Many times it may happen that all gates from the IC packages are not required to build the circuit and thus remaining gates are unused. Thus, the utility factor is very poor. This utility factor is more when we use only one logic gate (universal gate) to implement the entire logic circuit.

a. NAND Gate

• The NAND gate can be used to generate the NOT function, the AND function, the OR function and the NOR function.

NOT Function

• An inverter can be made from a NAND gate by connecting all of the inputs together and creating, in effect, a single common input, as shown in Fig. 3.9.2, for a two-input gate.

AND Function :

An AND function can be generated using only NAND gates. It is generated by simply inverting output of NAND gate; i.e. 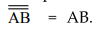 Fig. 3.9.3 shows the two input AND gate using NAND gates.

OR Function :

OR function is generated using only NAND gates as follows : We know that Boolean expression for OR gate is

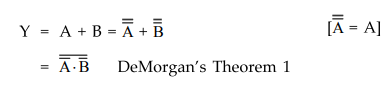
= A • B DeMorgan's Theorem 1

The above equation is implemented using only NAND gates as shown in the Fig. 3.9.4.

Note : Bubble at the input of NAND gate indicates inverted input.

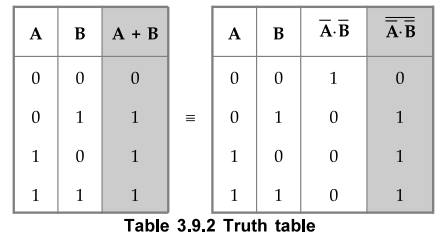
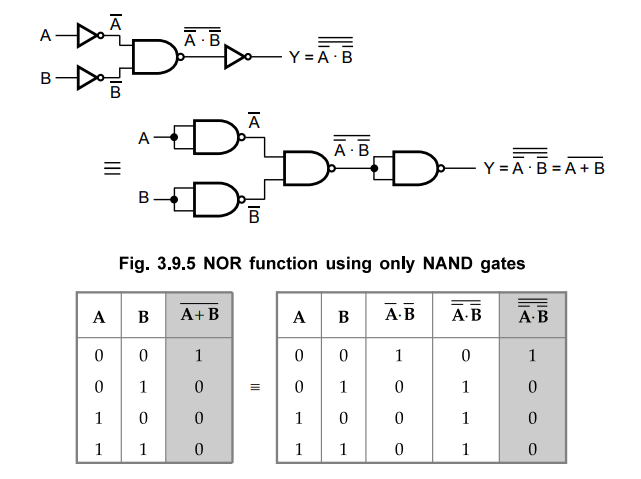
 NOR Function :

NOR function is generated using only NAND gates as follows : We know that Boolean expression for NOR gate is

The above equation is implemented using only NAND gates, as shown in the Fig. 3.9.5.

 

Examples for Understanding

Ex. 3.9.1 Implment EX-OR gate using only NAND gates.

Sol.:

The Boolean expression for EX-NOR gate is

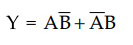
We can implement AND-OR logic by using NAND-NAND logic as shown in Fig. 3.9.6 (b)

 

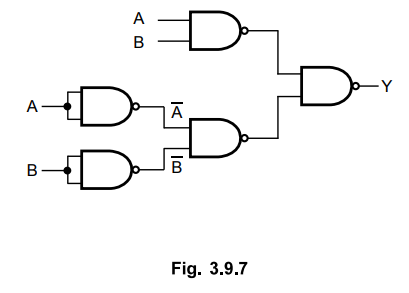
Ex. 3.9.2 Implement EX-NOR gate using only NAND gates.

Sol.:

The Boolean expression for EX-NOR gate is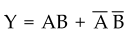 

EX-NOR gate using only NAND gates as shown in the Fig. 3.9.7.

 

Ex. 3.9.3 Construct the EX-OR gate using 4-NAND gates only, Boolean expression for EX-OR gate is .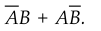

AU ; May-13, Marks 8

Sol. :

The above sum of product expression is implemented using NAND-NAND logic as shown in the Fig. 3.9.8.

b. NOR Gate

• Similar to NAND gate, the NOR gate is also a universal gate, since it can be used to generate the NOT, AND, OR and NAND functions.

NOT Function :

An inverter can be made from a NOR gate by connecting all of the inputs together and creating, in effect, a single common input, as shown in Fig. 3.9.9. 

OR Function :

• An OR function can be generated using only NOR gates. It can be generated by simply inverting output of NOR gate; i.e. 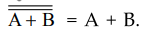. Fig. 3.9.9 (a) shows the two input OR gate using NOR gates.

AND Function :

• AND function is generated using only NOR gates as follows : We know that Boolean expression for AND gate is

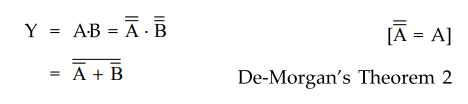
• The above equation is implemented using only NOR gates as shown in the Fig. 3.9.10.

Note : Bubble at the input of NOR gate indicates inverted input.

NAND Function :

NAND function is generated using only NOR gates as follows : We know that Boolean expression for NAND gate is

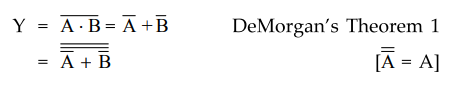
The above equation is implemented using only NOR gates, as shown in the Fig. 3.9.11.

 

Examples for Understanding

Ex. 3.9.4 Implement EX-NOR gate using only NOR gates.

Sol. : The Boolean expression for EX-NOR gate is :

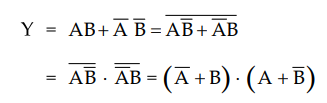
We can implement OR-AND logic by using NOR-NOR logic, as shown in Fig. 3.9.12 (b).

 

Ex. 3.9.5 Implement EX-OR gate using only NOR gates.

Sol. : Boolean expression of EX-OR gate

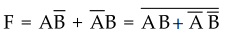
Complement of EX-NOR gate is EX-OR gate

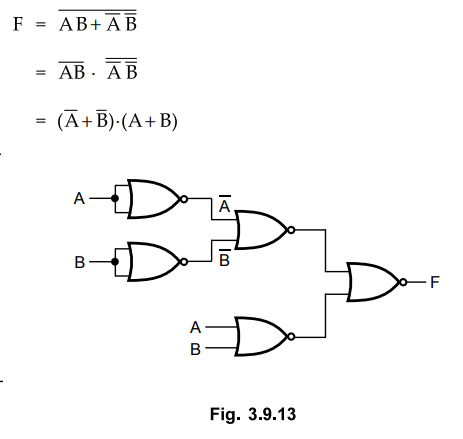
Note : We can implement OR-AND logic by NOR-NOR logic.

 

Ex. 3.9.6 Implement the following Boolean function with NAND-NAND logic

Y = AC + ABC + ABC + AB + D

Sol. :

Step 1 : Simplify the given Boolean function.

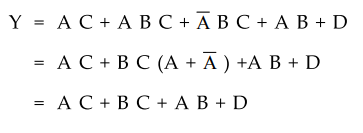
Step 2 : Implement using AND-OR logic.

 

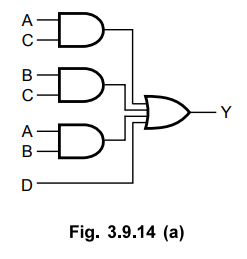
Step 3 : Convert AND-OR logic to NAND-NAND logic.

 

Ex. 3.9.7 Implement the following Boolean function ith NAND – NAND logic

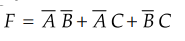
Sol. :

Step 1 : Implement Boolean function with AND-OR logic.

Step 2 : Convert AND-OR logic to NAND-NAND logic.

Note : It is possible to directly go to step 2 skipping step 1. Here, step 1 is included for clear understanding.

 

Ex. 3.9.8 Implement the following Boolean function with NOR-NOR logic

Y = AC + BC + AB + D.

Sol. :

Step 1 : Express Boolean function in POS form. Using duality theorem we get,

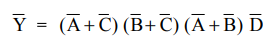
Step 2 : Implement Boolean function with OR-AND logic.

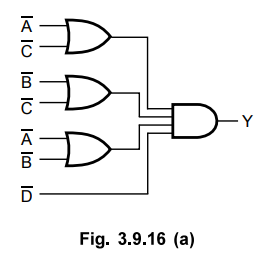
Step 3 : Convert OR-AND logic to NOR-NOR logic.

 

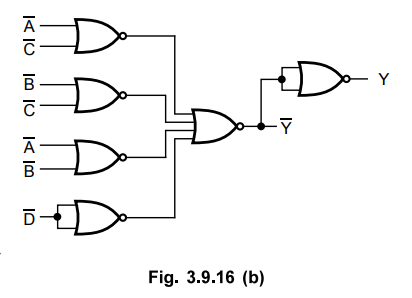
Ex. 3.9.9 Implement the following Boolean function with NOR-NOR logic

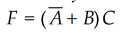
Sol. :

Step 1 : Implement Boolean function with OR-AND logic.

Step 2 : Convert OR-AND logic to NOR-NOR logic.

Note : It is possible to directly go to step 2 skipping step 1. Here, step 1 is included for clear understanding.

 

Ex 3.9.10 Simplify and implement the following SOP function using NOR gates,

f (A, B,C,D) = ∑ m (0, 1, 4, 5, 10, 11, 14, 15)

AU : May-12, Marks 10

Sol. :

Step 1 : Convert SOP function into its equivalent POS function.

∑ m (0, 1, 4, 5, 10, 11, 14, 15) = n M (2, 3, 6, 7, 8, 9, 12, 13)

Step 2 : K-map simplification :

Note We can convert OR-AND logic into NOR-NOR logic.

 

Ex. 3.9.11 Simplify and implement the following POS function using NAND gates,

f (A, B,C,D) = nM (0, 1, 2, 3, 12, 13, 14, 15)

Sol. :

Step 1 : Convert POS function into its equivalent SOP function.

II M (0, 1, 2, 3, 12, 13, 14, 15) = ∑ m (4, 5, 6, 7, 8, 9, 10, 11)

Step 2 : K-map simplification :

 

Ex. 3.9.12 Using K-map simplify the expression

Y(A, B, C, D) = m₁ + m₃ + m₅ + m₇ + m₈ + m₉ + m₀ + m₂ + m₁₀ + m₁₃

Indicate the prime implicants, essential and non-essential prime implicants. Draw the logic circuit using AND-OR-INVERT gates and also using NAND gates.

Sol. :

Logic circuit : Using NAND gate

We can implement AND-OR logic by using NAND-NAND logic

Ex. 3.9.13 Give the simplified expression for the following logic equation where d represents don't care condition.

f(A, B, C, D) = Σm(0, 8, 11, 12, 15) + d(1, 2, 4, 7, 10, 14)

Represent the simplified expression using logic gates.

Sol. : K-map Simplification :

 

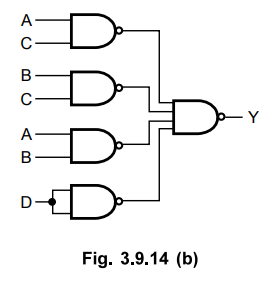
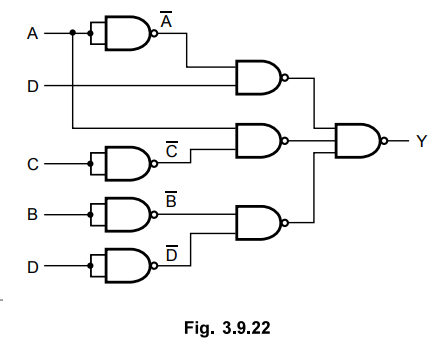
Ex. 3.9.14 Prove that 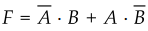  is exclusive OR operation and it equals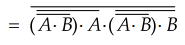 

Sol. : The truth table for expression 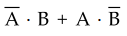 matches with the truth table for exclusive-OR gate and hence we can say the given expression represents exclusive-OR operation.

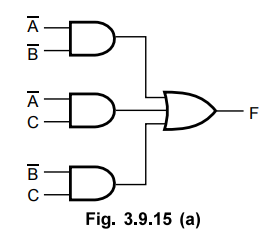
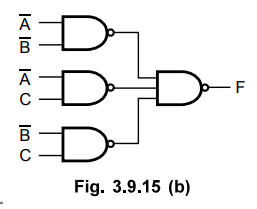
Ex. 3.9.15 Using K-map simplify the following function and implement the function using logic gates

f(A, B, C) = π(0, 4, 6).

Sol.

 

Examples for Practice

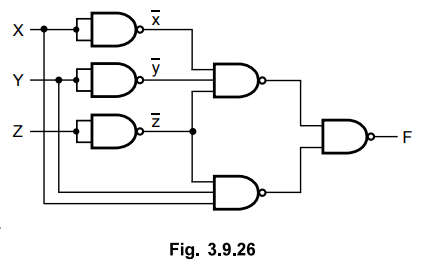
Ex. 3.9.16 Implement the following function with NAND gates. F(x,y,z) = (0,6)

Ans. :

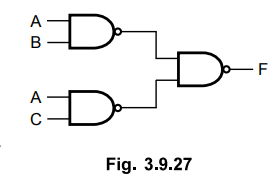
Ex. 3.9.17 Design a logic circuit to simulate the function (A, B, C) = A(B + C) by using only NAND gates.

Ans . :

Review Questions

1. Write the logic symbol, expression and truth table for the following logic gates :

1. i) EX-OR   ii) NOR    

2. i) NANO ii) EX-NOR

3. i) NAND   ii) NOR   iii) EX-OR

2. What are universal gates ? Give examples.

3. Why NAND and NOR gates are called universal gates?

4. Why digital circuits are more frequently constructed with NAND or NOR gates than with AND and OR gates ?

5. Realize i) AND gate ii) NOR gate using onl NAND gates.

6. Realize i) OR gate ii) EX-OR gate using NAND gates.

7. Realize i) OR gate ii) AND gate using only NOR gates.