Inductance of a Conductor

Inductance of a Conductor

Inductance of a conductor exists due to the flux distribution inside the conductor as well as the the flux distribution outside the conductor. Let us calculate inductance of a conductor due to internal as well as external flux.

1. Inductance of a Conductor due to the Internal Flux

Consider a long, straight conductor with radius r metres and carrying a current I amperes as shown in the Fig. 1.11.1 (a).

The magnetic field will be established due to this current. The magnetic flux lines will change inside the conductors which will contribute to induced voltage and hence inductance. The magnetic flux lines exist outside the conductor also. We may assume that the return path for the current in this conductor is far away and the magnetic field of the conductor is not affected. The value of inductance due to internal flux is given by the ratio of flux linkages to current by taking into account the fact that each line of internal flux links only a fraction of total current. The exact value of inductance of transmission line is obtained by considering the flux inside each conductor as well as external flux. The lines of flux are concentric with the conductor.

The m.m.f. in ampere turns around any closed path is equal to the current in amperes enclosed by the path. Thus we have

Let the magnetic field intensity at a point x meters from the center of the conductor be H_x. This is constant at all points as field is symmetrical. Thus integration of ds around the closed circular path is 2 π x

For the element having thickness dx, the flux will be product of Bx and the cross-sectional area of the element normal to the flux lines. This area is dx times axial length. If the axial length considered is 1 m then the flux per meter

d ϕ = B_x × 1 × dx = (µ × I / 2πr²) dx

This flux links with current I_x. Hence flux linkage per meter length of conductor of length is  given by

To find internal flux or the total linkage inside the conductor we have to carry the integration from the center of conductor to its outside edge.

Thus we have obtained inductance per unit length of a round conductor due to flux inside the conductor. Inductance per unit length is referred as simply inductance for convenience and simplicity.

2. Inductance of a Conductor due to External Flux

Now we shall estimate the flux linkages of the conductor due to the external flux. For this we will consider the flux linkages of an isolated conductor due to that portion of the external flux which lies between two points distant D₁ and D₂ meters from centre of conductor P₁ and P₂ are two such points as shown in the Fig. 1.11.2.

The conductor shown in the Fig. 1.11.2 carries current I. The flux paths are concentric circles around the conductor between P₁ and P₂.

Consider a tubular element which is x metres from center of conductor. The field intensity at this point is H_x. The m.m.f. around the element is

2πx x = I

The flux density B_x at this point is given by

The flux linkages dψ per meter are equal to dϕ since flux external to the conductor links all the current in the conductor. The total flux linkage between P₁ and P₂ are obtained by integrating dy from D₁ to D₂

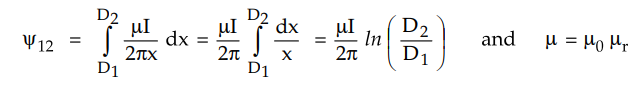
For relative permeability, µ_r = 1

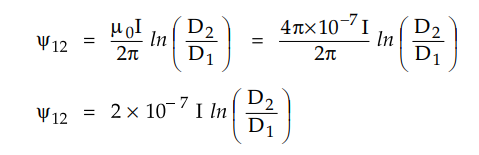
The inductance due to flux included between P₁ and P₂ only is,

If the external flux is considered to be extended from the surface of conductor to infinity then total flux linkages is given by,

Review Question

1. Derive the expression for internal and external flux linkage of a conductor carrying current I.

AU : Dec.-17, Marks 6