Inductance of a Single Phase Two Wire Line

Inductance of a Single Phase Two Wire Line

AU : May-05, 07, 08, Dec.-15, 17

Consider a single phase line consisting of two parallel conductors. These conductors are forming a rectangular loop of one turn. These conductors are solid conductors of radii rx and r2 respectively. One conductor is forming a return circuit for the other. The two conductors are carrying currents I₁ and I₂ respectively.

In a single phase circuit we have

 I₁ + I₂ — 0

I₂ = -I₁

Here we are neglecting the effect of earth's presence of magnetic field geometry as earth's relative permeability is same as that of air and its conductivity is relatively small.

The arrangement of the conductors and variation of flux density due to each conductor is shown in the Fig. 1.12.1 respectively.

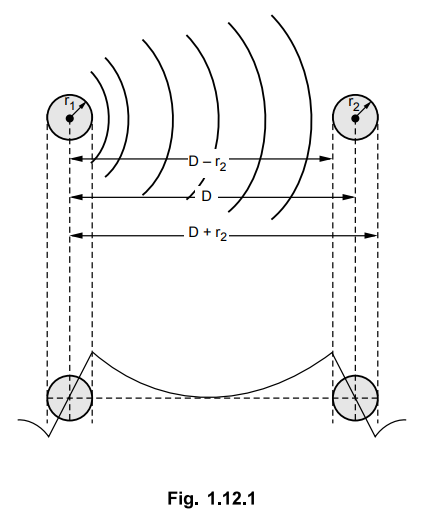
In the beginning, let us consider only the flux linkages of the circuit caused by the current in conductor 1. The flux line set up by the current flowing in conductor 1 at a distance equal to or greater than D + r₂ from the center of conductor 1 does not link the circuit and hence is not responsible for inducing any voltage in the circuit. This is because conductor 2 carries current which is equal and opposite to that in conductor 1.

The external flux from r₁ to D-r₂ links all the current I₁ in conductor 1. Over the surface of conductor 2 i.e. between (D - r₂) and (D + r₂), the external flux links a current whose magnitude is progressively reduces from I₁ to zero because of negative current in conductor 2.

The total inductance of the current carrying in conductor 1 can be calculated by assuming that D is much greater than r₁ and r₂. Under this condition it can be assumed that flux from (D - r₂) to the centre of conductor 2 links current Ij and flux from the centre of conductor 2 to (D + r₂) links zero current.

The inductance due to current in conductor 1 can be calculated by using the relation,

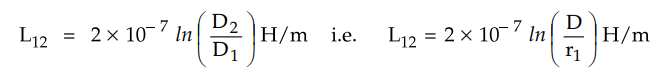
This expression is valid for external flux only. For internal flux we have,

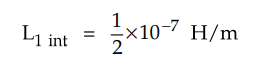
The total inductance of the circuit due to current in conductor 1 only is,

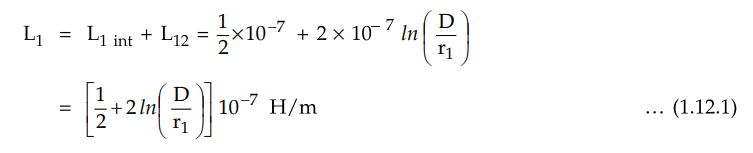
The above equation can conveniently be written as,

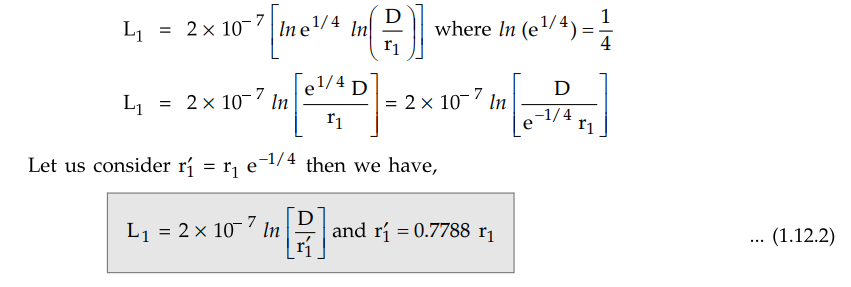
The radius r₁ is that of an imaginary or fictitious conductor assumed to have no internal flux. The quantity ε^-1/4 equals to 0.7778.

The radius r₁ is called Geometric Mean Radius (GMR) of a conducter.

The value of inductance given by equation (1.12.2) is same as that given by equation (1.12.1). The difference is that equation (1.12.2) omits the term on account of internal flux. But it is compensated by adjusted value of radius of conductor.

The above equation is derived by considering solid round conductors. Equation (1.12.2)      is algebraic manipulation of equation (1.12.1). Hence the multiplying factor of 0.7778 is applicable only to solid round conductors in order to account for internal flux. 

The conductor 2 carries current in opposite direction to that in conductor 1. The flux linkages produced by current in conductor 2 considered alone are in the same direction as those produced by current in conductor 1.

The resultant flux for the two conductors is determined by sum of m.m.f.s of the two conductors. If permeability is assumed to be constant then the flux linkages and inductances of the two conductors calculated separately may be added.

The inductance of conductor 2 in comparison with equation (1.12.2) can be written as,

The above equation gives the inductance of two wire single phase line taking into consideration the flux linkages caused by current in both the conductors.

The value of inductance obtained is the inductance per loop meter or per loop mile. The inductance given by equation (1.12.2) is one half of the total inductance of single phase line and is called inductance per conductor.

Example 1.12.1 A two conductor single phase line operates at 50 Hz. The diameter of each conductor is 20 mm and the spacing between the conductor is 3 m. Calculate

i) The inductance of each conductor per km.

ii) The loop inductance of the line per km.

iii) The inductive reactance per km.

Solution :

Example 1.12.2 A single phase transmission line has two parallel conductors 3 m apart, the radius of each conductor being 1 cm. Calculate the loop inductance per km length of the line if the material of the conductors is 1) copper 2) steel with relative permeability of 100.

AU : May-07, Marks 8

Solution :

Review Questions

1. Derive the equation for inductance of single phase two wire line.

2. A single phase line has two parallel conductors 2 meters apart. The diameter of each conductor is 1.2 cm. Calculate the loop inductance per km of the line.       

(Ans.: 2.423 mH)

3. A single phase transmission line has two parallel conductors 3 m apart. The radius of each conductor being 1 cm. Calculate the loop inductance per km length of the line if the material of conductor is copper.      

(Ans.: 26.5877 × 10^-4 H/km)

4. Compute the inductance of a single phase line consisting of conductors of 4 mm diameter each. The spacing between conductors is 1 m. The line is overhead line and has a length of 5 km.

(Ans.: 0.0129 H)