Inductance of Composite Conductor Lines

Inductance of Composite Conductor Lines

Now we will consider a single phase 2 wire system. It consists of two conductors say P and Q which are composite conductors. The arrangement of conductors is shown in the Fig. 1.14.1.

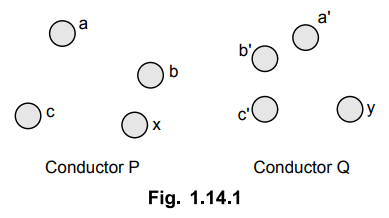
Conductor P is consisting of x identical, parallel filaments. Each of the filament carries a current of I/x. Conductor Q consists of y filament with each filament carrying a current of -I/y. The conductor Y carries a current of I amps in opposite direction to the current in conductor X as it is forming return path.

The flux linkages of filament say a due to all currents in all the filaments is given by

The conductor P consists of x number of parallel filaments. If all the filaments are of equal inductances then inductance of the conductor would be 1/x times inductance of one filament. All the filaments have different inductances but the inductance of all of them in parallel is 1/x times the average inductance.

Inductance of conductor P is given by,

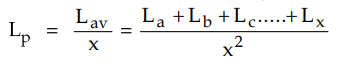
Substituting the values of L_a, L_b  .... L_x in the equation and simplifying the expression we have,

In the above expression the numerator of argument of logarithm is the xy, the root of xy terms. These terms are nothing but products of distances from all the x filaments of conductor P to all the y filaments of the conductor Q.

For each filament in conductor P there are y distances to filaments in conductor Q and there are x filaments in conductor P. The xy terms are formed as a result of product of y distances for each of x filaments. The xy^th root of the product of the xy distances is called the geometric mean distance between conductor P and Q. It is termed as D_m or GMD and is called mutual GMD between the conductors.

The denominator of the above expression is the x² root of x² terms. There are x filaments and for each filament there are x terms consisting of r' (denoted by D_aa,D_bb etc.) for that filament times the distances from that filament to every other filament in conductor P.

If we consider the distance D_aa then it is the distance of the filament from itself which is also denoted as 1^. This r' of a separate filament is called the self GMD of the filament. It is also called geometric mean radius GMR and identified as D_s.

Thus the above expression now becomes

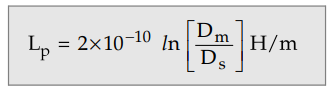
Comparing this equation with the expression obtained for inductance of a single phase two wire line. The distance between solid conductors of single conductor line is substituted by the GMD between conductors of the composite conductor line. Similarly the GMR (rQ of the single conductor is replaced by GMR of composite conductor.

The composite conductors are made up of number of strands which are in parallel. The inductance of composite conductor Q is obtained in a similar manner. Thus the inductance of the line is,

L = L_p + L_Q 

Example 1.14.1 In a single phase line as shown in Fig. 1.14.2 conductors a and a' in parallel form one conductor and conductors b and b' in parallel form the return path. Calculate the total inductance of the line per km assuming that current is equally shared by the two parallel conductors: conductor dia 2 cm.

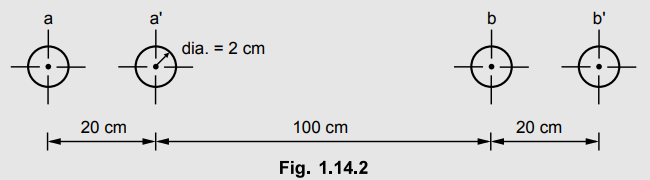
Solution : Distance between conductor a - a' = 20 cm

Diameter of each conductor = 2 cm, Radius of each conductor = 1 cm

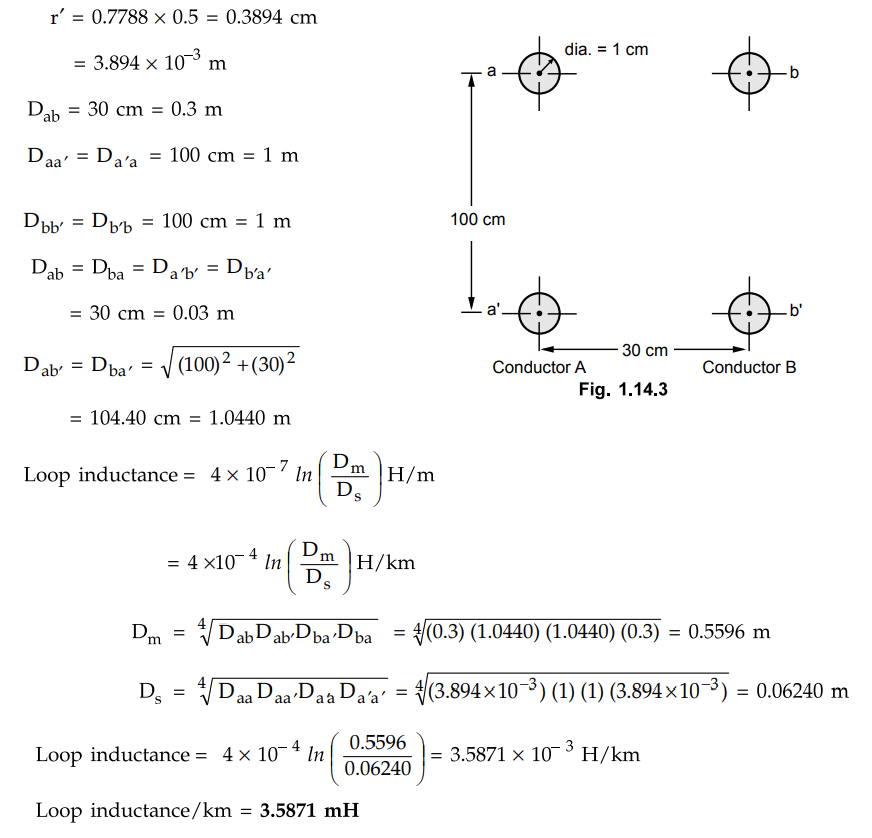
Example 1.14.2 Two conductors of a single phase line, each of 1 cm diameter are arranged in a vertical plane with one conductor mounted 1 m above the other. A second identical line is mounted at the same height as the first and spaced horizontally 30 cm apart from it. The upper and lower conductors are connected in parallel. Determine the inductance per km of the resulting double circuit.

Solution : The Fig. 1.14.3 shows the arrangement of conductors. Diameter of each conductor = 1 cm. Radius of each conductor = 0.5 cm.

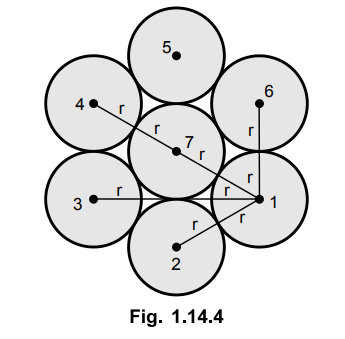
Example 1.14.3 Calculate the GMR of a conductor having seven strands each of 3 mm radius.

Solution : Seven stranded conductor is as shown in the Fig. 1.14.4.

Review Questions

1. Derive the expression for the inductance of composite conductor lines.

2. Prove that the inductance of a group of parallel wires carrying current can be represented in terms of their geometric distances.

3. Write a short note on concept of GMR and GMD.

4. Distinguish between GMD and GMR.