Inductance of Three Phase Line with Unsymmetrical Spacing but Transposed

Inductance of Three Phase Line with Unsymmetrical Spacing but Transposed

Now consider a three phase line having three conductors but not spaced equilaterally. The problem of finding the inductance in this case is difficult. The flux linkage and the corresponding inductance will not be same in each phase. Due to this different inductance per phase there is imbalance in the circuit though the currents in each phases are balanced.

The drops in the three phases due to these inductances are observed to be different. Thus at the receiving end we will not get the same voltage.

In order to achieve balance under this case, transposition of transmission line is preferred after a certain fixed distance. This is shown in the Fig. 1.19.1.

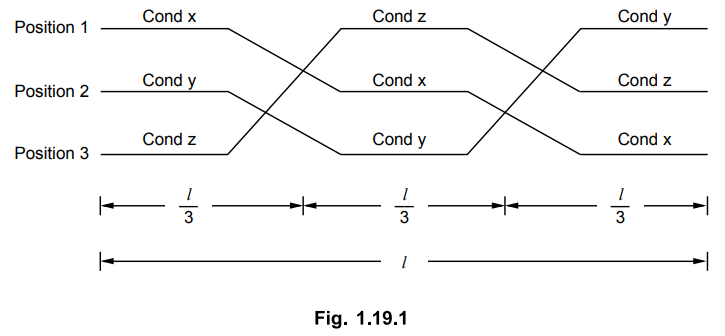
The positions of the conductors are exchanged at regular interval along the line so that each conductor occupies the original position of every other conductor over an equal distance. This exchange of conductor positions is called transposition. Thus balance in the three phase is restored. 

The Fig. 1.19.2 shows complete transposition cycle. The conductors in the individual phases are denoted by x, y and z where the positions are given by 1, 2, and 3. The same average inductance over the complete cycle is obtained due to the transposition.

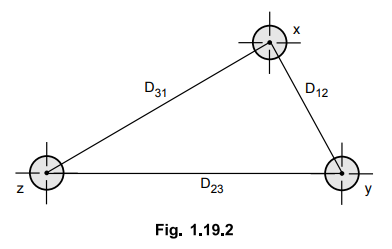
The average inductance of one conductor is obtained by finding the flux linkages of a conductor for each position that is occupied during a complete cycle of transposition. Then the average flux linkages are obtained.

Now let us find the flux linkages of conductor x which is in position 1 whereas conductor y and z are in positions 2 and 3 respectively.

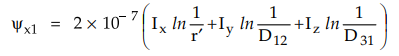
Conductor x is in position 2 whereas conductors y and z are in positions 3 and 1 respectively.

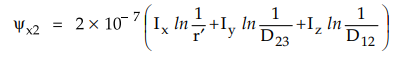
Conductor x is in position 3 whereas conductor y and z are in positions 1 and 2 respectively.

In modern power lines, transposition of lines is not done at regular intervals even though an exchange in conductor positions can be made at switching stations to balance the inductance per phase. The inequality in the phases of an untransposed line is small and neglected in many cases.

If the dissymmetry is neglected, the inductance of the untransposed line is the average value of the inductive reactance of one phase of the same line correctly transposed.

Example 1.19.1 A three phase transmission line has conductor diameter of 1.24 cm each, the conductors being spaced as shown in the Fig. 1.19.3. The line is carrying balanced load and it is transposed. Find the inductance of the line per km per phase.

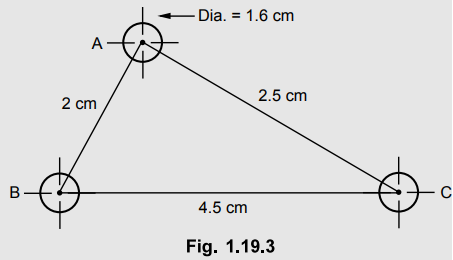
Solution :

Example 1.19.2 A three phase transmission line has conductor diameter of 1.6 cm each, the conductors being spaced as shown in the Fig. 1.19.4. The loads are balanced and the line is transposed. Find the inductance per phase per km of the line and inductive reactance.

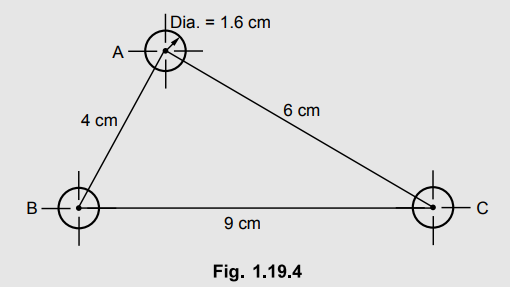
Solution :

Example 1.19.3 A three phase line with equilateral spacing of 6 m is to be rebuilt with horizontal spacing with central conductor is midway between the outers. The conductors are to be fully transposed. Determine the spacing between adjacent conductors such that the new line has the same inductance as the original line.

Solution : Consider the three phase line with equilateral spacing. Let us find the inductance of this line.

D = Distance between the conductors 

= 6 m

Let r be the radius of each of the conductors.

The inductance of the line per phase per km is given by,

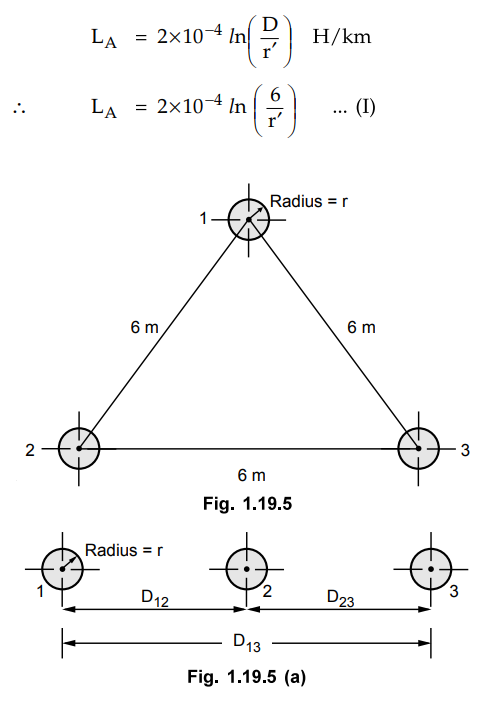
This line is to be rebuilt with horizontal spacing such that

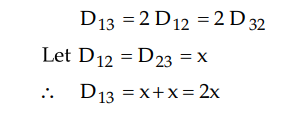
The radius of the conductor remains same as r.

The inductance per phase per km with this arrangement is given by,

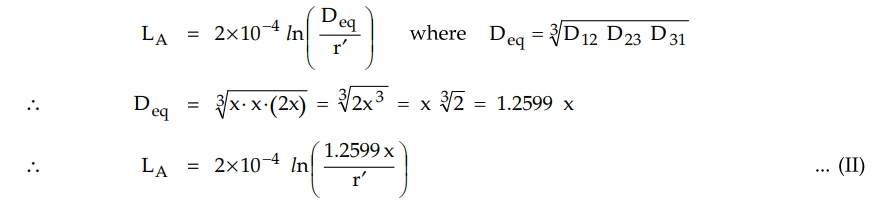
Equating equations (I) and (II) as the inductance in both the arrangements remains same.

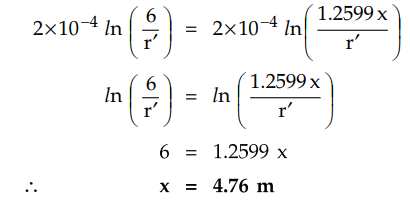
Example 1.19.4 The three conductors of a 3 phase 50 Hz line are arranged with the spacing A - B - 3 m, B - C - 5 m, C - A - 3.2 m. Calculate the inductance and inductive reactors per phase per km of the line. The diameter of each conductor is 25 mm.

 Solution :

Example 1.19.5 A 50 Hz overhead transmission line consisting of 3 conductors each of diameter 1.24 cm and spaced 2m apart. Calculate the inductance per phase per km for the following arrangement between conductors :

1) Equilateral spacing 2) Horizontal spacing.

Assume transposed line.

Solution : First let's consider the equilateral spacing of conductors.

D = Distance between the conductors = 2 m.

Radius of conductor = Diameter of conductor / 2

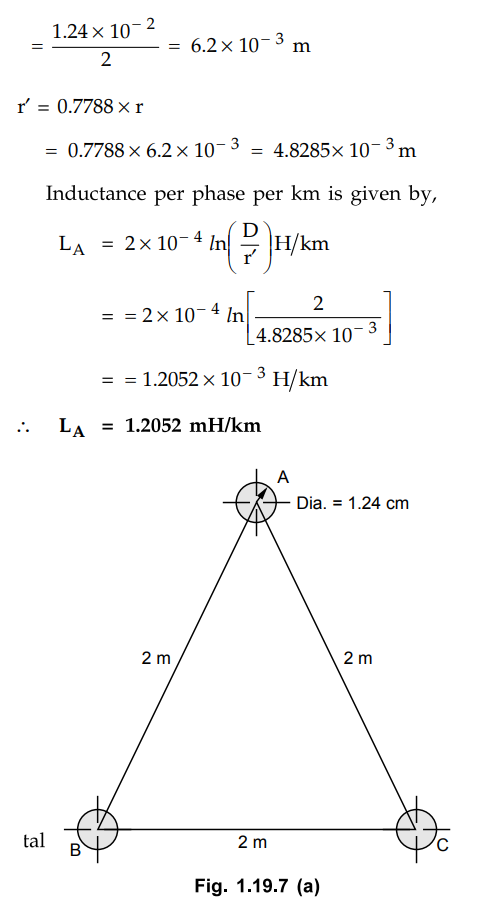
ii) Now let us consider the horizontal spacing of conductors

Example 1.19.6 Determine the inductance of a 3 phase, line operating at 50 Hz and the conductors are arranged as shown in Fig. 1.19.8. The conductor diameter is 0.7 cm.

AU : May-05, May-17, Marks 8

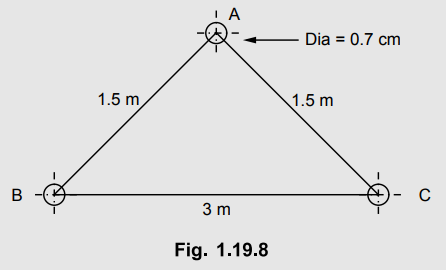
Solution :

Example 1.19.7 A 3 phase 3 wire over head line consist of 2.5 cm diameter conductors in horizontal configuration. The line is supplying a balanced load.

i) Find the inductance of each phase conductor/km length

ii) Why are the inductance of the 3 phases different

iii) What is the significance of imaginary terms in the expression Assume that the line is not transposed. Interface spacing is 3 m.

AU : May-10, Marks 16

Solution :

Since the line is not transposed and the flux linkage in the three phases are not same, the inductance in all three phases are not same.

The imaginary part in the expression for inductance represents exchange of energy between phases. It is power transferred between phases by mutual induction.

The negative imaginary component shows power is supplied that phase to other phases. The positive imaginary component shows the power is received by that phase from other phases. Total power transferred in any case in zero. The mutual power transfer does not affect the power dissipated in various conductors forming the system. 

Review Questions

1. Derive the expression for inductance per phase of a three-phase overhead transmission line with unsymmetrical spacing between conductors (with transposition).

2. The three conductors of a three phase line are arranged at the corners of triangle of sides 4, 5 and 6 metres. Calculate the inductance per km of each conductor when conductors are regularly transposed. The diameter of each line conductor is 2 cm.         [Ans.: 1.285 mH]

3. Derive expression for the inductance of a 3 phase line with conductors untransposed. What is the significance of imaginary term in the expression for inductance ? Hence derive the expressions for inductance for a completely transposed line.