Introduction to Combinational Logic Circuit

Introduction to Combinational Logic Circuit

AU : Dec.-07, 08

• When logic gates are connected together to produce a specified output for certain specified combinations of input variables, with no storage involved, the resulting circuit is called combinational logic circuit. In combinational logic circuit, the output variables are at all times dependent on the combination of input variables.

• A combinational circuit consists of input variables, logic gates, and output variables. The logic gates accept signals from the input variables and generate output signals. This process transforms binary information from the given input data to the required output data. Fig. 3.10.1 shows the block diagram of a combinational circuit. As shown in Fig. 3.10.1, the combinational circuit accepts n-input binary variables and generates output variables depending on the logical combination of gates.

Review Question

1. What is combinational logic circuit ?

1. Design Procedure

AU : Dec.-07, 08

• The design of combinational circuits starts from the outline of the problem statement and ends in a logic circuit diagram or a set of Boolean functions from which the logic diagram can be easily obtained. The design procedure of the combinational circuit involves following steps :

1. The problem definition.

2. The determination of number of available input variables and required output variables.

3. Assigning letter symbols to input and output variables.

4. The derivation of truth table indicating the relationships between input and output variables.

5. Obtain simplified Boolean expression for each output.

6. Obtain the logic diagram.

Example for Understanding

Ex. 3.10.1 Design a combination logic circuit with three input variables that will produce a logic 1 output when more than one input variables are logic 1.

Sol. :

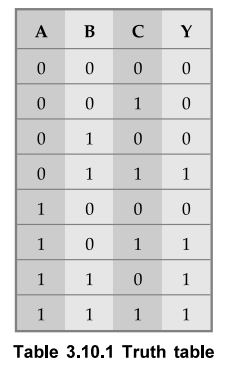
Step 1 : Derive the truth table for given statement. Given problem specifies that there are three input variables and one output variable. We assign A, B and C letter symbols to three input variables and assign Y letter symbol to one output variable. The relationship between input variables and output variable can be tabulated as shown in truth Table 3.10.1.

Step 2 : Obtain simplified Boolean expression.

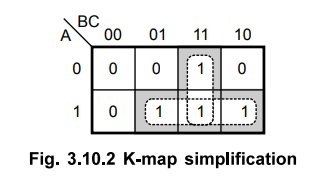
 Now we obtain the simplified Boolean expression for output variable Y using K-map simplification.

Y = AC + BC + AB

Step 3 : Draw logic diagram.

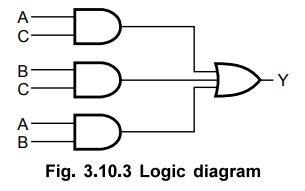
In this chapter we are going to study various combinational circuits using above illustrated design method.

Examples with Solutions

Ex. 3.10.2 A majority gate is a digital circuit whose output is equal to 1 if the majority of inputs are 1 's. The output is 0 otherwise. Using a truth table, find the Boolean function implemented by a 3-input majority gate. Simplify the function and implement with gates.

AU : Dec.-07, Marks 8

Sol. :

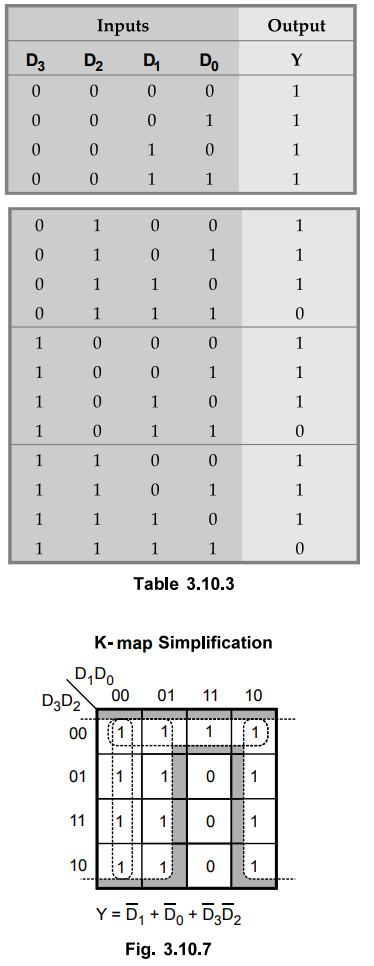
Ex. 3.10.3 The inputs to a circuit are the 4 bits of the binary number D3D2D1D0. The circuit produces a 1 if and only if all of the following conditions hold.

1) MSB is 'T or any of the other bits are a '0'.

2) D₂ is a 1 or any of the other bits are a '0'.

3) Any of the 4 bits are a 0.

Obtain a minimal expression for the output.

AU : Dec.-08, Marks 8

Sol. : The truth table for the given problem is as shown in Table 3.10.3.

Review Question

1. Explain the design procedure for combinational circuits.