Iterative Methods

ITERATIVE METHODS

The types of iterative methods are

(a) Gauss-Jacobi method 

(b) Gauss-Seidel method

 

(a) Jacobi method of iteration or Gauss-Jacobi method

We shall explain this method in the case of three equations in three unknowns.

Consider the system of equations,

Then, iterative method can be used for the system (1). Solve for x, y, z (whose coefficients are the largest values) in terms of the other variables.

Continuing in the same way, if the th iterates are x^(r), y^(r), z^(r), the iteration scheme reduces to

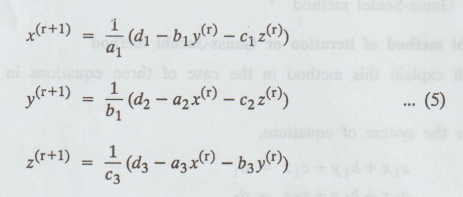
The procedure is continued till the convergence is assured (correct to required decimals).

 

(b) Gauss-Seidel method of iteration

This method is only a refinement of Gauss-Jacobi method. As before,

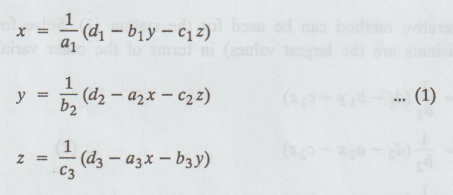
We start with the initial values y⁽⁰⁾, z⁽⁰⁾ for y and z and get ⁽¹⁾ from the first equation. That is,

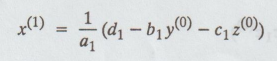
While using the second equation, we use z⁽⁰⁾ for z and x⁽¹⁾  for x instead of x⁽⁰⁾  as in the Jacobi's method, we get

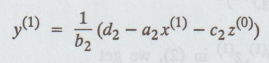
Now, having known x⁽¹⁾ and y⁽¹⁾, use x⁽¹⁾  for x and y⁽¹⁾  for y in the third equation, we get

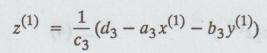
To find the value of the unknowns, we use the latest available values on the right hand side. If x(t), y(t), z(r) are the rth iterates, then the iteration scheme will be

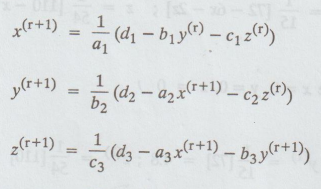
This process of iteration is continued until the convergence is confirmed. As the current values of the unknowns at each stage of iteration are used in getting the values of unknowns, the convergence in Gauss-Siedel method is very fast when compared to Gauss-Jocobi method and this method is roughly two times faster than that of Gauss-Jacobi method.

Note: We emphasize, however, that without diagonal dominance, neither Jacobi nor Gauss-Seidal is sure to converge. When both methods converge, the Gauss-Seidel method converges faster. Data (1995) discusses this and gives examples.

Note on Diagonally dominant: When the system of equations can be ordered so that each diagonal entry of the coefficient matrix is larger in magnitude than the sum of the magnitudes of the other coefficients in that row, such a system is called diagonally dominant.

1. Solve the following system of equations by Gauss-Jacobi method and Gauss-Seidel Method. TELS-01] [A.U. May 1999, A.U. M/J 2006]

27x + 6y - z = 85

x + y + 54z = 110

6x + 15y + 2z = 72

[A.U CBT M/J 2010]

[A.U A/M 2011]

[A.U Tvli. A/M 2011]

[A.U M/J 2013, N/D 2006, M/J 2012, N/D 2012] [A.U ND 2017 R13, A/M 2018 R13] [A.U A/M 2019 R-17] [A.U N/D 2020 (R-17)] [A.U A/M 2021 (R-17)]

Solution :

Note :

(1) Solve by using calculator and cross check your answer.

(2) Fix 3 decimal places in your calculator.

We get x = 2.425, y = 3.573, z = 1.926

As the coefficient matrix is not diagonally dominant we rewrite the equations.

27x + 6y-z = 85; 6x+15y + 2z = 72; x+y+54z = 110

Since, the diagonal elements are dominant in the coefficient matrix, we write x, y, z as follows:

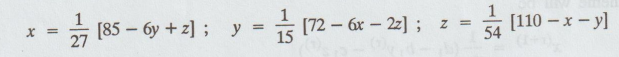
(1) Gauss-Jacobi method

Let the initial values be x = 0, y = 0, z = 0

First iteration :

Second iteration :

Third iteration :

Fourth iteration :

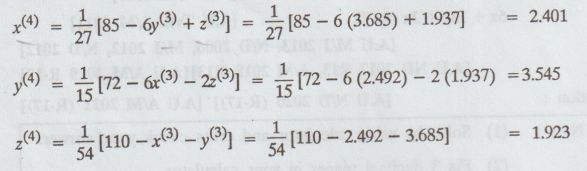
Fifth iteration :

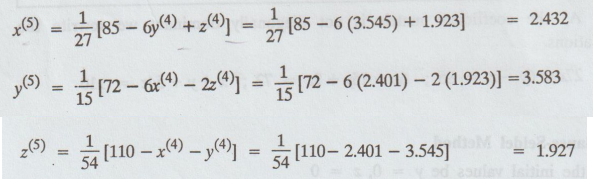
 Sixth iteration :

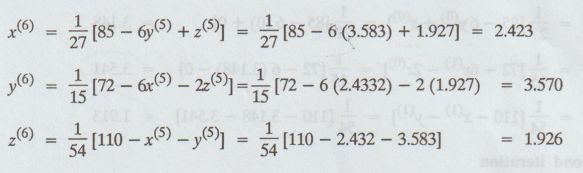
Seventh iteration :

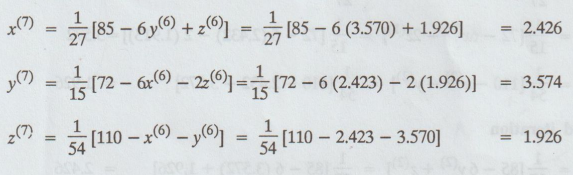
Eighth iteration :

Ninth iteration

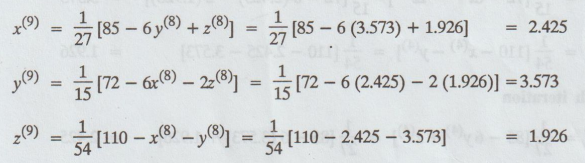
Eighth iteration and Ninth iteration coinsides.

Hence, x = 2.425, y = 3.573, z= 1.926

Correct to three decimal places.

2. Gauss-Seidel Method

Let the initial values be y = 0, z = 0

First iteration

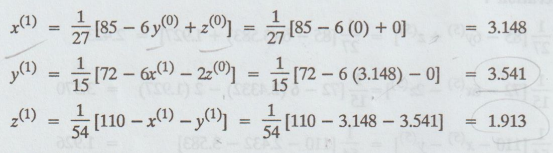
Second iteration

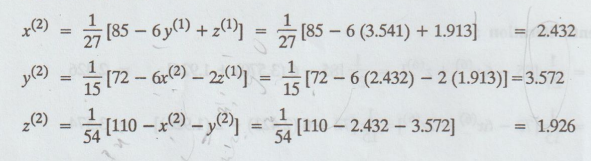
Third iteration

Fourth iteration

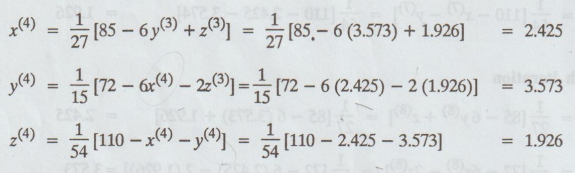
Fifth iteration

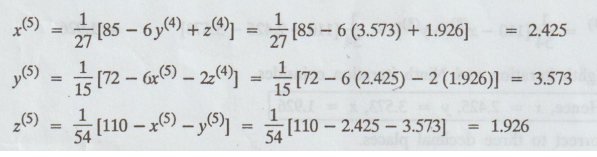
Fourth iteration values = Fifth iteration values.

Hence, x = 2.425, y = 3.573, z = 1.926

This shows that the convergence is rapid in Gauss-Seidel Method when compared to Gauss-Jacobi method.

 

2. Solve the following equations by Gauss-Seidel method

4x + 2y + z = 14, x + 5y - z = 10, x + y + 8z = 20  [A.U. April/May 2005, M/J 2014] [A.U A/M 2015 (R8-10)] [A.U N/D 2015 (R8-10)] [A.U A/M 2017 R-8]

Solution :

Note :

(1) Solve by using calculator and cross check your answer.

(2) Fix 2 decimal places in your calculator.

We get x = 2.00, y = 2.00, z = 2.00

As the coefficient matrix is diagonally dominant solving for x,y,z we get

First iteration

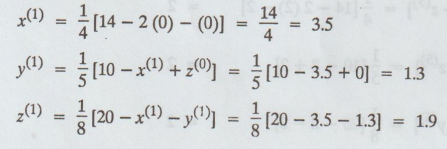
Second iteration

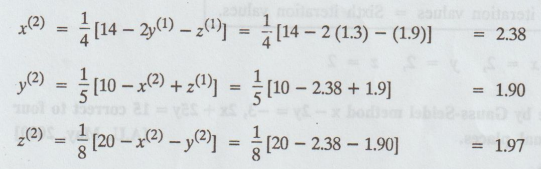
Third iteration

Fourth iteration

Fifth iteration

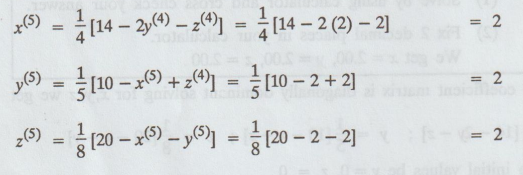
Sixth iteration

Fifth iteration values = Sixth iteration values.

Hence, x = 2, y = 2, z = 2

 

3. Solve by Gauss-Seidel method x-2y=-3, 2x + 25y = 15 correct to four decimal places. ([A.U. May, 2000]

Solution :

Note :

(1) Solve by using calculator and cross check your answer.

(2) Fix 4 decimal places in your calculator.

We get x = -1.5518, y = 0.7241

First Iteration :

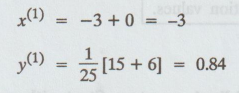
Second iteration :

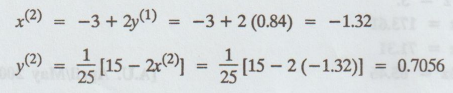
Third iteration :

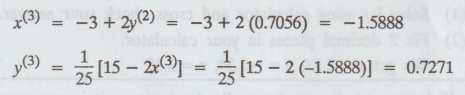
Fourth iteration :

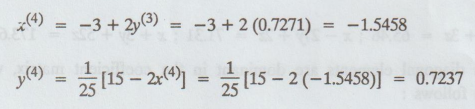
Fifth iteration :

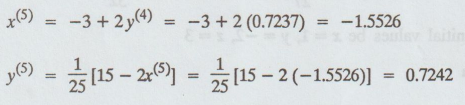
Sixth iteration :

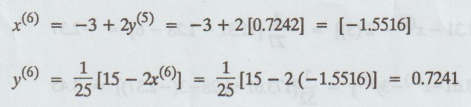
Seventh iteration :

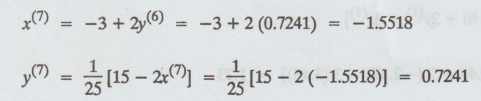
Eighth iteration :

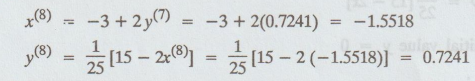
Seventh iteration values = Eighth iteration values.

Hence, x = -1.5518, y = 0.7241

 

4. Using Gauss-Seidel method, solve the following system. Start with

x = 1, y = -2, z = 3.

x + 3y + 52z = 173.61 –

x - 27y + 2z = 71.31

41x - 2y + 3z = 65.46

[A.U. April/May 2004]

Solution :

Note :

(1) Solve by using calculator and cross check your answer.

(2) Fix 2 decimal places in your calculator.

We get x = 1.23, y = -2.34, z = 3.45 - 2

As the coefficient matrix is not diagonally dominant as it is, we rewrite the equation.

41x - 2y + 3z = 65.46; x - 27y + 2z = 71.31; x + 3y + 52z = 173.61

Now, the diagonal elements are dominant in the coefficient matrix, we write x, y, z as follows :

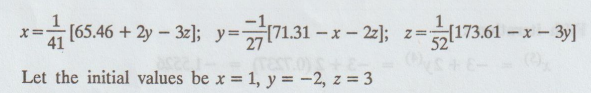
Let the initial values be x = 1,y =- 2, z = 3

First Iteration

Second Iteration

Third Iteration

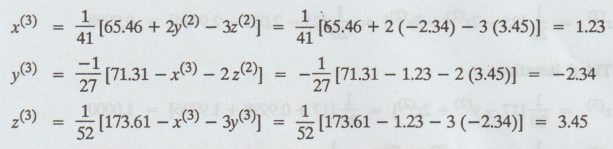
Second iteration values = Third iteration values.

Hence, the result of x = 1.23, y = -2.34, z = 3.45

 

5. Solve the given system of equations by using Gauss-Seidal iteration method.

20x + y = 2z = 17

3x + 20y z = -18

2x - 3y + 20z = 25

[A.U. N/D 2003] [A.U. Tvli N/D 2010]

[A.U M/J 2009, N/D 2009, N/D 2010]

[A.U M/J 2012, N/D 2014] [A.U N/D 2016 R8-10, M/J 2016 R8-10, N/D 2016 R-13] [A.U A/M 2018 R-13 NM]

Solution :

Note :

(1) Solve by using calculator and cross check your answer.

(2) Fix 4 decimal places in your calculator.

We get x = 1.0000, y=-1.0000, z= 1.0000+x0s

As the coefficient matrix is diagonally dominant solving for x, y, z we get

Let the initial values be y = 0, z = 0

First iteration

Second iteration

Third iteration

Fourth iteration

Third iteration values = Fourth iteration values.

Hence x = 1, y = -1, z = 1

 

6. Solve the system by Gauss Seidal iteration method :

20x + 4y - z = 32, x + 3y + 10z = 24, 2x + 17y + 4z = 35 [A.U N/D 2021 (R-17)]

Solution :

Note :

(1) Solve by using calculator and cross check your answer.

(2) Fix 3 decimal places in your calculator.ev silini or 10

We get x = 1.398, y = 1.466, z = 1.820

As the coefficient matrix is diagonally dominant solving for x, y, z we get

Let the initial values be y = 0, z = 0

First iteration :

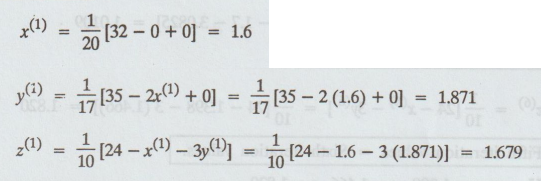
Second iteration :

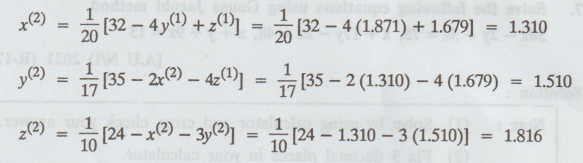
Third iteration :

Fourth iteration :

Fifth iteration:

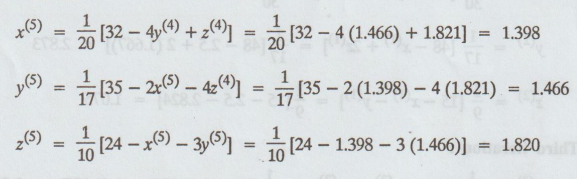
Sixth iteration :

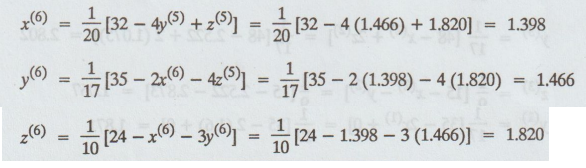
Fifth iteration values = Sixth iteration values. Sixth iteration values.

Hence, x = 1.398, y = 1.466, z = 1.820

 

7. Solve the following equations using Gauss Jacobi method.

30x - 2y + 3z75, x + 17y - 2z = 48, x + y + 9z = 15

[A.U N/D 2021 (R-17)]

Solution :

Note:

(1) Solve by using calculator and cross check your answer.

(2) Fix 3 decimal places in your calculator.

We get x = 2.580, y = 2.798, z = 1.069

As the coefficient matrix is diagonally dominant solving for x, y, z we get

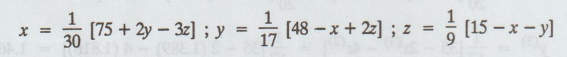
Let the initial values be x = 0, y = 0, z= 0

First iteration :

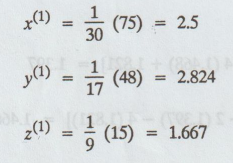
Second iteration :

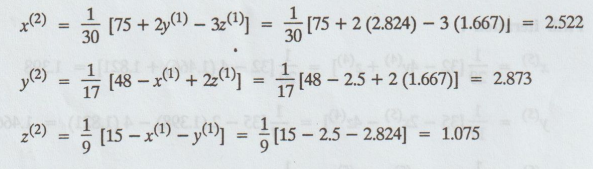
Third iteration :

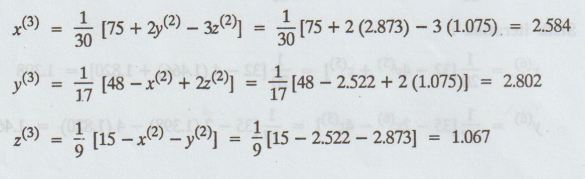
Fourth iteration :

Fifth iteration :

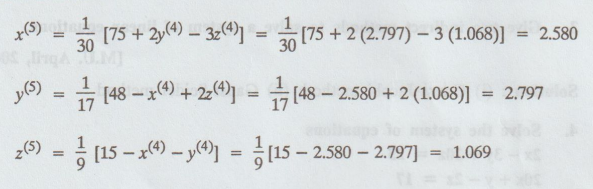
Sixth iteration :

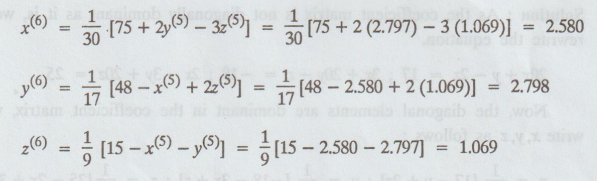
Seventh iteration :

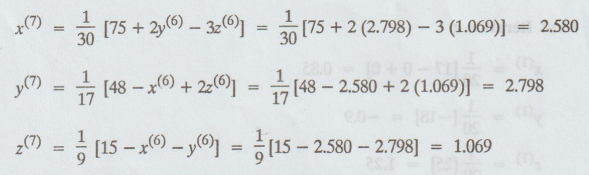
Sixth iteration values = Fifth iteration values.

Hence, x = 2.580, y = 2.798, z = 1.069