Kelvin’s Law

Kelvin’s Law

A transmission line can be designed by taking into consideration various factors out of which economy is the most important factor. The conductor which is to be selected for a given transmission line must be economical. Most of the part of total line cost is spent for conductor. Thus it becomes vital to select most economic size of conductor.

The most economic design of the line is that for which total annual cost is minimum. Total annual cost is divided into two parts viz. fixed standing charges and running charges.

The fixed charges include the depreciation, the interest on capital cost of conductor and maintenance cost. The cost electrical energy wasted due to losses during operation constitutes running charges.

The capital cost and cost of energy wasted in the line is based on size of the condcutor. If conductor size is big then due to its lesser resistance, the running cost (cost of energy due to I²R losses) will be lower while the conductor may be expensive. For smaller size conductor, its cost is less but running cost will be more as it will have more resistance and hence greater I²R losses.

The cost of energy loss is inversely proportional to the conductor cross section while the fixed charges (cost of conductor, interest and depreciation charges) are directly proportional to area of cross section of the conductor. Mathematically we have, 

Annual interest and depreciation cost = S₁

S₁ ∝ a

a is area of cross section of conductor

S₁ = K₁ a

Annual cost of energy loss in line = S₂

S₁ ∝ 1/a

S₂ =  K₂ / a

Here K₁ and K₂ are constants

S = Total annual cost

S = S₁ + S₂

S = K₁ a + K₂ / a

For economical design of line, the cost will be minimum for a particular value of area of cross-section 'a' of the conductor.

Thus for economic design, dS / da = 0

Thus the most economical conductor size is one for which annual cost of energy loss is equal to annual interest and depreciation on the capital investment of the condcutor material. This is known as Kelvin's law. The most economical current density can be estimated by using this law as it is not sufficient to determine cross section of the conductor.

Let us find economic current density :

Let     R = Resistance of the conductor of 1 mm² cross section and 1 km length.

I = RMS value of current in the conductor throughout the year

a = Area of cross section of the conductor in mm²

w = Weight of conductor of 1mm2 cross section in kgf/km

C₁ = Cost of electrical energy wasted in rupees per kWh

C₂ = Cost of conductor in kgf in rupees.

t = Total number of working hours per year

r = Rate of interest and depreciation in percentage on capital cost.

Cost of one km conductor = Rs aw C₂

The economical cross section is one for which fixed annual charges on conductor material should be equal to cost of energy wasted during the year.

The graphical representation of Kelvin's law is shown in the Fig. 7.9.1.

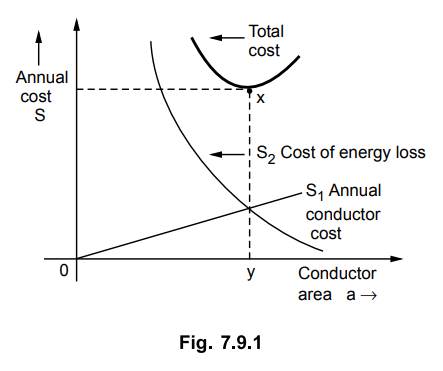
As the annual conductor cost S₁ is directly proportional to area of cross section of conductor, it is represented by straight line while the cost of energy wasted is inversely proportional to conductor area so it is represented by rectangular hyperbola. The total annual cost S is summation of S₁ and S₂ for that cross section.

The lowercost point x on the total annual cost curve S gives the most economical area of conductor which corresponds to point of intersection of two components of total cost S as S₁ and S₂ as shown in the graph. At this point of intersection, S₁ and S₂ are equal. So most economical area is 0y while corresponding minimum cost is xy.

 

1. Limitations of Kelvin's Law

Following are limitations in applying Kelvin's law.

1. The amount of energy loss can not be determined accurately as the load factors of the losses and the load are not same. Also the future load conditions and load factors can not be predicted exactly.

To estimate the energy loss approximately, the load curves are drawn for various types of loads and the load factor is determined. From the load factor, one can get the information of average load current carried by the line during the entire year. The total losses in the year are proportional to the mean value of the square of current during that year. The square root of the mean value of the squares of the line currents throughout the year is called rms current.

If I_max = Maximum full load line current

K_L = Annual load factor of the line   = Average load over a period  / Maximum load over the period 

= Number of kWh (units) generated per year / Maximum demand (kW) × 8760 (hrs)

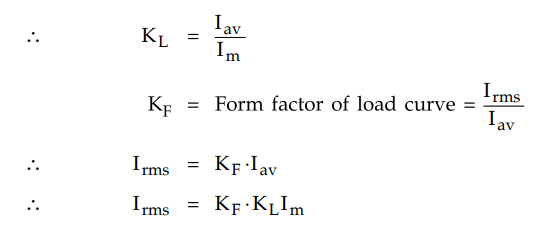
The rms current obtained from above expression gives fairly accurate results.

The load factor of the losses is different from the load factor of the load current. The load factor of the losses is called loss factor λ. It is defined as ratio of actual energy loss during a period to the energy loss if maximum current is flowing during the whole period.

2. The cost of energy loss can not be determined exactly. The cost of losses per unit is more than the generating cost per unit.

3. The cost of conductor and rates of interest are changing continuously.

4. If economical conductor size is selected then voltage drop may be beyond the acceptable limits.

5. The economical size of conductor may not have the enough mechanical strength.

6. The cost of conductor also includes to some extent cost of insulation which changes with change in cross section of conductor. The cost of insulation is difficult to express in terms of cross section of conductor.

7. Due to problem of corona, leakage currents, the economic size of conductor can not be used at extra voltages.

8. Due to change in rates of interest and depreciation continuously, even if other parameters are same, application of Kelvin's law will give economical conductor size different at different time and in different countries.

9. In case of cables, the current carried safely depends on accepted temperature rise. In addition to copper loss, there is dielectric loss in metalllic sheath all the time independent of whether current is carried by cable or not. These losses are difficult to consider these losses while applying Kelvin's law.

In case of overhead lines, the problem of temperature rise is not much dominent than in case of cables. The I2R losses are the major losses in overhead lines. So Kelvin's law gives fairly acceptable results for lines upto 33 kV. 

For cables, the economic conductor size as obtained from Kelvin's law is to be considered from the point of view of acceptable temperature rise. So the practically selected conductor size and size obtained from Kelvin's law will be different and the difference in cost will not be considerable. So small deviations from most economic conductor size can be always made practically.

10. The conductor size of the two systems having same load demand should also be same. But the cost of energy, interests and depreciation rates which are independent of resistance, voltage drop, temperature rise may be different in the two systems may give different economic cross section of the conductor after applying Kelvin's law.

 

2. Modified Kelvin’s Law

Due to limitations of applying Kelvin's law, some modification is necessary which was suggested by G. Kapp. While considering the cost of conductor, the cost associated with poles or towers, insulators, erection is not considered in case of overhead line while for underground cable, the cost of cable insulation and laying is not considered which forms appreciable part in the total cost in actual practice. With increase in conductor size, there is increase in mechanical stresses which needs stronger towers and insulators. This increases cost of labour for erection.

To account for these costs and to get fair results practically, G. Kapp suggested to divide the initial investment into two parts i) one part which is independent of conductor size and ii) other part directly proportional to the conductor cross section.

The initial investment

S₁ = K₀ + K₁a

Annual cost of line, S₁ = (K₀ + K₁a) r if r is rate of interest and depreciation

Annual cost of power loss

S₁ = K₂ / a

Total annual cost,

S = S₁ + S₂

S = (K₀ + K₁a) r + K₂ / a

For minimum cost,

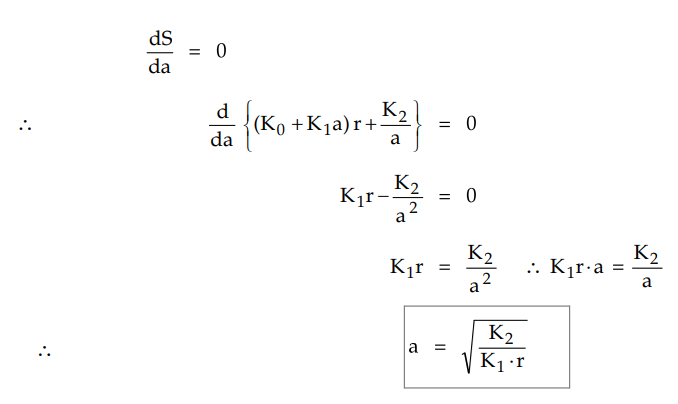
Thus modified Kelvin's law suggests the most economical conductor size is one for which annual energy loss cost is equal to annual cost of interest and depreciation for that part of initial investment which is proportional to area of conductor.

The graphical representation of modified Kelvin's law is shown in the Fig. 7.9.2.

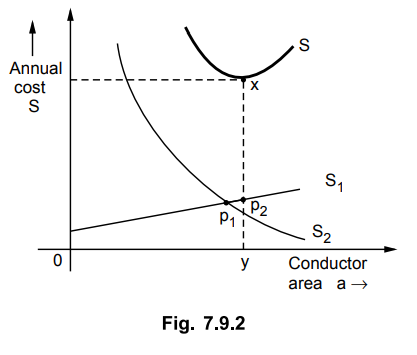
The cost S₁ is represented by straight line. Its intercept on cost axis gives that part of annual cost which is not proportional to conductor area. The lost energy cost curve S₂ is represented by rectangular hyperbola as before. The summation curve of these two costs is shown by S.

The lowermost point on total cost curve x gives minimum cost (xy) and economical conductor size (0y). The length P₁P₂ is the cross section of the conductor cost which is not proportional to area of cross section of the conductor.

 

Examples with Solutions

 

Example 7.9.1 A 3 core, 11 kV cable supplies a load of 1600 kW at a p.f. of 0.8 lag for 320 days in a year at an average of 10 hours per day. The capital cost per km of the cable is Rs. 10000 + 20,000 a. The resistance per km of a cable of cross sectional area of 1 cm² is 0.173 Ω. If the cost of energy per unit is 5 paise and the rate of interest and depreciation is 10 %. Calculate the most economical current density and diameter of the conductor. 

Solution : Current in each conductor can be calculated as,

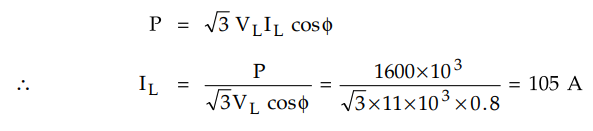
If R is resistance of each conductor then total copper loss are given by,

Total copper loss in all 3 conductors = 3 I²R = 3 (105)² R = 33075R W

For cross sectional area of conductors as 'a' cm² and length of line as 1 km

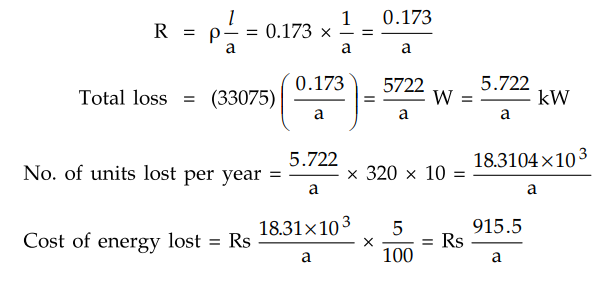
Part of annual charges due to interest and depreciation on capital cost which is proportional to cross sectional area of conductor is given by

Cost due to interest and depreciation = Rs (20,000 ×10 / 100)        

= Rs 2000 a

According to Kelvin's law the most economical conductor size is given by,

Most economical current density = I_L / a = 105 / 0.6765 = 155.21 A / cm²

 

Example 7.9.2 Determine the best current density in Amps/mm2 for a three phase overhead line. The line is in use for 2600 hours per year and if the conductor costs Rs. 3.0/kg. It has a specific resistance of 1.73 × 10^-8 Ω-m and weighs 6200 kg/m³. Cost of energy is 10 paise/unit. Interest and depreciation is 12 % of conductor costs.

Solution : Cost of conductor = Rs. 3 per kg

If l is length of conductor in m and a is area of cross section in m² of conductor then Volume of each conductor in m³ = l.a.

Weight of each conductor = l.a.× 6200 - 6200 l.a. kg.

Capital cost of conductor = Rs. 3 × 6200 l.a.

Annual interest and depreciation

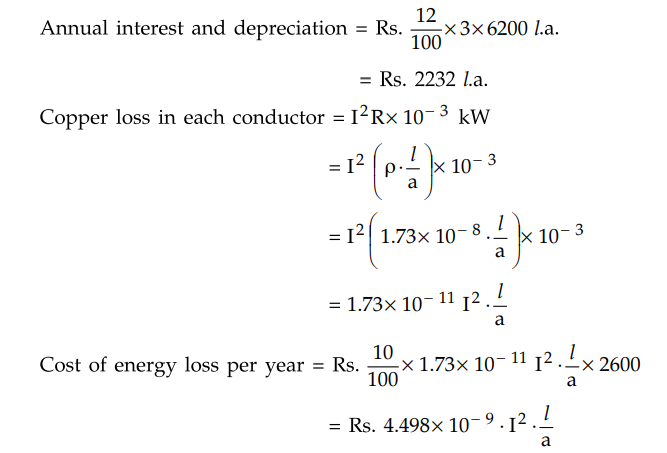
According to Kelvin's law, for best current density, cost of energy loss per year must be equal to annual cost due to interest and depreciation.

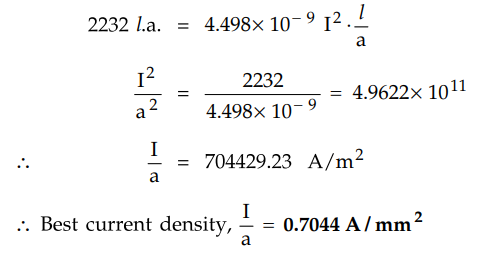
Part of annual cost due to interest and depreciation which is proportional to conductor cross section is given by,

Annual const due to interest and depreciation = 2000 A × 12/ 100 = 240 A

Resistance of conductor = 0.17 / A Ω

According to Kelvin's law, cost of energy loss should be equal to cost due to interest and depreciation,

Economical current density = 94.63 A/cm²

Review Questions

1. State the Kelvin's law and obtain the expression for the economic current density.

2. State and explain the limitations cf Kelvin's Law.

3. State and explain modified kelvin’s Law.