Large sample test (Normal distribution) for single mean

Large sample test

Large sample test (Normal distribution) for single mean

If the size of the sample n > 30, then that sample is called large sample.

 

1. Tests on the mean of a Normal distribution, if σ is known.

If x₁, x₂,...,x_n is a random sample of size n from a normal population with mean µ and s.d σ, then the sample mean is  and s.d is σ/√n

Thus, the standard normal variate corresponding to  is

Set up a null hypothesis H₀ : μ = μ₀ and

Alternative hypothesis H₁ : μ ≠ μ₀ where μ₀ is a specified constant.

 

2. Tests on the mean of a Normal distribution,

if σ is unknown.

We can use its estimate of the sample s.d as σ = s and the test statistic

Note: General procedure for Hypothesis tests [A.U N/D 2014]

1. From the problem context, identify the parameter of interest.

2. State the null hypothesis, Ho.

3. Specify an appropriate alternative hypothesis, H1

4. Choose a significance level a.

5. Determine an appropriate test statistic.

6. State the rejection region for the statistic.

7. Compute any necessary sample quantities, substitute these into the equation

for the test statistic, and compute the value.

8. Conclusion: Decide whether or not, Ho should be rejected and report that in the problem context.

 

Working Procedure :

For the large sample (n> 30), to test whether the population mean μ equals to a constant μ₀ or not.

1. Null hypothesis H₀: μ = μ₀

(i) If we want to test the significance of the difference between  and μ, then we set up the null hypothesis H₀ : μ =  [the difference is not significant]

(ii) If we want to test any statement about the population, then we set up the null hypothesis, that is true.

For example, if we want to find the population mean has specified value µ₀, then H₀ : µ = µ₀

2. Alternative hypothesis H₁:

u ≠ μ₀ (two-tailed) (or)

μ > μ₀ one-tailed (right) (or)

μ < μ₀ one-tailed (left)

(i) Suppose, the average life of the company bulbs has been estimated (µ) 3000 hours. We take a sample from the population and suppose the sample mean is () 2950 hours. We want to decide whether the mean life time has changed.

Here, H₀ : μ = 3000

H₁ : μ ≠ 3000 [two-tailed test]

(ii) The mean life of bulbs to be atleast 3000 hours and the sample mean is 2950 hours.

Here, H₀ : µ = 3000

H₁ μ < 3000 [one-tailed test (left)]

(iii) The mean life of bulbs more than 3000 hours and the sample mean is 2950 hours.

Here,

Ho: μ = 3000

H₁ μ > 3000 [one tailed test (right)]

3. Level significant : ɑ

4. Critical region:

(a) If u ≠ μ₀, then the test is two-tail test for the given ɑ.

The critical values are -Zɑ/2 and Zɑ/2

(b) If µ > µ₀, then the test is one-tailed test (right) for the given ɑ.

The critical value is Zɑ

(c) If µ < µ₀, then the test is one-tailed test (left) for the given ɑ.

The critical value is -Zɑ

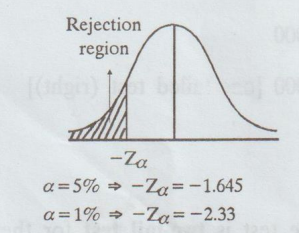
5. The test statistic

[For large sample s nearly equal to σ]

where

  → mean of the sample

μ → population mean

σ → population standard deviation

n → sample size.

6. Conclusion:

 (a) If - Z_ɑ/2 < Z < Z _ɑ/2, then we accept H₀ for two-tailed test; otherwise, reject H₀.

 (b) If Z_ɑ  > Z, then we accept H₀ for one-tailed test (right); otherwise, reject H₀.

(c) If - Z_ɑ < Z, then we accept Ho for one-tailed test (left); otherwise, reject H₀.

 

Example 1.2a(1).

A sample of 900 members has a mean 3.4 cm and standard deviation 2.61 cm. Is the sample from a large population of mean 3.25 cms and standard deviation of 2.61 cms? (Test at 5% level of significance. The value of z at 5% level is | Z_ɑ | < 1.96) [A.U M/J 2010] [A.U A/M 2010 (R-08)] [A.U N/D 2016 (R13)]

Solution: Given: n = 900, μ = 3.25, s = 2.61,  = 3.4, ɑ = 5%

 

Example 1.2.a(2)

The mean life time of a sample of 100 light bulbs produced by a company is computed to be 1570 hours with a standard deviation of 120 hours. If μ is the mean life time of all the bulbs produced by the company, test the hypothesis μ = 1600 hours, against the alternative hypothesis μ 1600 hours with ɑ = 0.05 and 0.01. [A.U. A/M 2003] [A.U N/D 2020 & 2021 (R-17)] 1600, s = 120, x = 1570,

Solution :

Given: n = 100, μ  = 1600 s = 120   = 1570, α = 0.05 and α = 0.01

 

Example 1.2a (3).

The mean breaking strength of the cables supplied by a manufacturer is 1800 with a S.D. of 100. By a new technique in the manufacturing process, it is claimed that the breaking strength of the cable has increased. In order to test this claim, a sample of 50 cables is tested and it is found that the mean breaking strength is 1850. Can we support the claim at 1% level of significance ?

Solution:

Given: n = 50, μ = 1800, s = 100,    = 1850, ɑ = 1%

6. Conclusion :

Here Cal Z > table Z

i.e., 3.54 > 2.33

So, we reject H₀.

i.e., We may support the claim of increase in breaking strength.

 

Example 1.2a(4).

A normal population has a mean of 6.48 and s.d of 1.5. In a sample of 400 members mean is 6.75. Is the difference significant ?

Solution :

Given: n = 400, μ = 6.48, s = 1.5,   = 6.75

 

Example 1.2.a(5)

The average number of defective articles per day in a certain factory is claimed to be less than the average of all the factories. The average of all the factories is 30.5. A random sample of 100 days showed the following distribution.

Is the average less than the figure for all the factories ?

Solution :

 

Example 1.2.a(6)

A sample of 100 people during the past year showed an average life span of 71.8 years. If the s.d. of the population is 8.9 years, test whether the mean life span today is greater than 70 years. [A.U. 2009]

Solution:

Given: n = 100,   = 71.8, μ = 70, σ = 8.9

 

Example 1.2.a(7)

The guaranteed average life of a certain type of electric light bulbs is 1000 hours with a standard deviation of 125 hours. It is decided to sample the output so as to ensure that 90 percent of the bulbs do not fall short of the guaranteed average by more than 2.5%. What must be the minimum size of the sample? [A.U CBT A/M 2011]

Solution:

Here μ= 1000 hours, σ = 125 hours.

Since, we do not want the sample mean to be less than the guaranteed average mean (u= 1000) by more than 2.5%, we should have

Let n be the given sample size. Then,

According to the given condition, we have

P (Z > - √n/5) = 0.90 ⇒ P (0 < Z < √n/5) = 0.40

√n/5 = 1.28 (From Normal probability tables)

⇒ > n = 25 × (1.28)² = 41 approximately

 

Example 1.2.a(8)

A survey is proposed to be conducted to know the annual earnings of the old Statistics graduates of Delhi University. How large should the sample to taken in order to estimate the mean annual earnings within plus and minus Rs. 1,000 at 95% confidence level? The standard deviation of the annual earnings of the entire population is known to be Rs. 3,000.

Solution:

 Given: σ = Rs. 3,000

We know that, in sampling from normal population or for large samples from any population 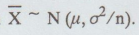 Hence, from normal probability tables, we have:

 

Example 1.2a (9)

A normal population has a mean 0.1 and S.D 2.1. Find the probability that mean of a sample of size 900 will be negative.

Solution:

Given: μ = 0.1, s = 2.1, n = 900