Large sample test for difference of proportions

Large sample test for difference of proportions

Suppose we want to compare 2 district populations with regard to possession of an attribute. Let a sample of size n₁ be chosen from the first population and another sample of size n2 be chosen from the second population. Let X₁ be the number of persons possessing the attribute A in the first sample and let X₂ be the number of persons possessing the same attribute in the second sample.

Then p₁ = X₁ /  n₁ p₂ = X₂ / n₂

As before E(p₁) = P₁ and E(p₂ ) = P₂ where P₁ and P₂ are the proportions in the populations.

V(p₁ ) = P₁ Q₁ / n₁ and V(p₂) = P₂ Q₂ / n₂

Since for large samples p₁ and p₂ are asymptotically normally distributed P₁-P₂ is also normally distributed, and also v

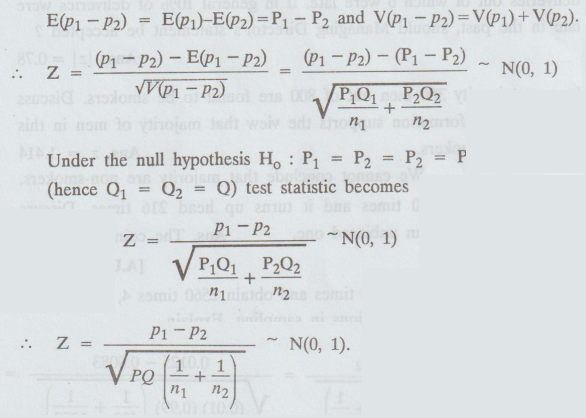
An unbiased estimate of population proportion P based on both the samples is given by P = n₁p₁ + n₂p₂ / n₁+ n₂ Suppose the population proportions

P₁ and P₂ are given to be different. (i.e.,) P₁ ≠ P₂. If we want to test whether the difference P₁ - P₂ is significant then the test statistic becomes

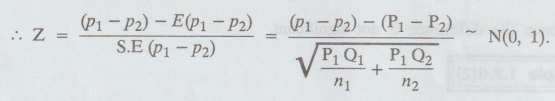
Here sample proportions are not given. If we set up a null hypothesis Ho: P1 P2 then test statistic becomes

 

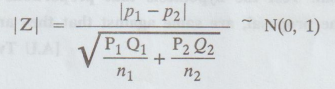
Example 1.2.d(1)

During a country wide investigation the incidence of TB was found to be 1%. In a college of 400 strength 5 were reported to be affected whereas in another college of 1200 strength 10 were reported to be affected. Does this indicate any significant difference.

Solution:

Given:

P = 1%  1 / 100 = 0.01; Q = 1 - 0.01 = 0.99

n₁=400; n₂=1200; P₁ 5/400 =0.0125; P₂ = 10 / 1200 = 0.0083

1. H_o : P₁ = P₂ [no significant difference]

2. H₁ : P₁ ≠ P₂

3. α = 0.05

4. Table value

|Z| = 1.96 at 5% level.

5. Calculate :

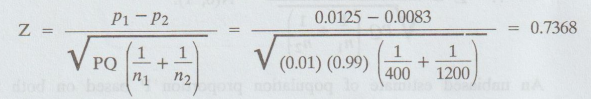
6. Conclusion:

Here, Cal Z < table Z

i.e., 0.7368 < 1.96

So, we accept H₀ at 5% level of significance.

Hence the difference is not significant.

 

Example 1.2.d (2)

Random samples of 400 men and 600 women were asked whether they would like to have a flyover near their residence. 200 men and 325 women were in favour of the proposal. Test the hypothesis that proportions of men and women infavour of the proposal, are same against that they are not, at 5% level. [A.U Tvli M/J 2011]

Solution:

Given:

6. Conclusion:

Here, Cal Z < table Z

i.e., 1.269 < 1.96

So, we accept Ho at 5% level of significance.

Hence we may conclude that men and women do not differ significantly as regards proposal of flyover is concerned.

 

Example 1.2.d(3) d

A company has the head office at Calcutta and a branch at Bombay. The personnel director wanted to know if the workers at the two places would like the introduction of a new, plan of work and a survey was conducted for this purpose. Out of a sample of 500 workers at Calcutta, 62% favoured the new plan. At Bombay out of a sample of 400 workers, 41% were against the new plan. Is there any significant difference between the two groups in their attitude towards the new plan at 5% level.

Solution:

Given:

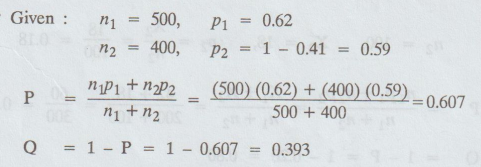
1. H₀ P₁ = P₂ [there is no significant difference between the two groups in their attitude towards the new plan]

2. H₁ : P₁ ≠ P₂ [Two-tailed]

3. ɑ =  0.05

4. Table value |Z| = 1.96

5. Calculate :

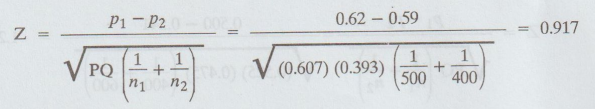
6. Conclusion:

Here, Cal Z < table Z

i.e., 0.917 < 1.96

So, we accept Ho at 5% level of significance.

Hence we conclude that there is no significant difference between the two groups in their attitude towards the new plan.

 

Example 1.2.d(4)

A cigarette manufacturing firm claims that its brand A of the cigarettes outsells its brand B by 8%. If it is found that 42 out of a sample of 200 smokers prefer brand A and 18 out of another random sample of 100 smokers prefer brand B, test whether the 8% difference is a valid claim. (use 5% level of significance).

Solution:

Given:

6. Conclusion :

Here, Cal Z < table Z

i.e., 1.02 < 1.96

So, we accept Ho at 5% level of significance.

Hence we may conclude that a difference of 8% in the sale of two brands of cigarettes is a valid claim by the firm.

 

Example 1.2.d(5)

A machine produced 20 defective units in a sample of 400. After overhauling the machine, it produced 10 defective units in a batch of 300. Has the machine improved in production due to overhauling. Test it at 5% level of significance. [A.U. May 2001]

Solution:

Given: n₁ = 400, n₂ = 300

6. Conclusion :

Here, Cal Z < table Z

i.e., 1.1 < 1.645

So, we accept Ho at 5% level of significance.

The machine has not improved after overhauling.

 

Example 1.2.d(6)

In two large populations, there are 30 and 25 per cent respectively of blue-eyed people. Is this difference likely to be hidden in samples of 1,200 and 900 respectively from the two populations ?

Solution:

Given: n₁ = 1200, n₂ = 900

P₁ = Proportion of blue-eyed people in the first population

= 30%  = 0.30

P₂ = Proportion of blue-eyed people in the second population

= 25% = 0.25

Q₁ = 1 - P₁ = 0.30 = 0.70

Q₂ =  1 – P₂ = 1 – 0.25 – 0.75

1. H₀ : P₁ =  P₂, the sample proportions are eqaul

2. H₁: P₁ ≠  P₂

3. α = 5%

4. Table value |Z| =1.96

5. Calculate :

Conclusion:

Here, Cal Z > table Z

i.e., 2.56 > 1.96

So, we reject Ho at 5% level of significance.

We conclude that the difference in population proportions is unlikely to be hidden in sampling.

 

Example 1.2.d(7)

In a random sample of 400 students of the university teaching departments, it was found that 300 students failed in the examination. In another random sample of 500 students of the affiliated colleges, the number of failures in the same examination was found to be 300. Find out whether the proportion of failures in the university teaching departments is significantly greater than the proportion of failures in the university teaching departments and affiliated colleges taken together.

Solution:

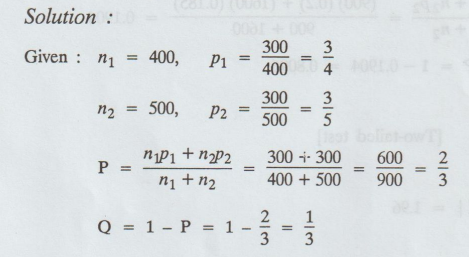
1. H₀ :  P = p₁ [P is the pooled estimate]

i.e., proportion of failures in the university teaching departments and affiliated colleges taken together, do not differ significantly]

2. H₁ : P ≠ P₁

3. ɑ is not given

4. Table value |Z| = 3 (for general) [both the level of significance]

5. Calculate :

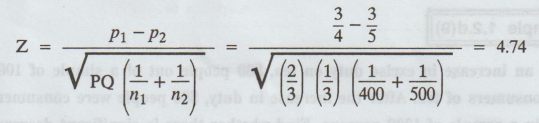
6. Conclusion:

Here, Cal Z > table Z

i.e., 4.74 > 3

So, we reject H₀

We conclude that there is significant difference between p₁ and P.

 

Example 1.2.d(8)

In a large city A, 20 per cent of a random sample of 900 school boys had a slight physical defect. In another large city B, 18.5 percent of a random sample of 1600 school boys had the same defect. Is the difference between the proportion significant?

Solution :

6. Conclusion:

Here Cal Z < table 2

i.e., 0.92 < 1.96

So, we accept Ho at 5% level of significance.

 

Example 1.2.d(9)

Before an increase in excise duty on tea, 800 people out of a simple of 1000 were consumers of tea. After the increase in duty, 800 people were consumers of tea in a sample of 1200 persons. Find whether there is significant decrease in the consumption of tea after the increase in duty.

Solution :

6. Conclusion:

Here, Cal Z > table Z

i.e., 6.82 > 2.3

So, we reject Ho at 1% level of significance.

 

EXERCISE 1.2(d),

1. In a city A, 20% of a random sample of 900 school boys had a certain slight physical defect. In another city B, 18.5% of a random sample of 1600 school boys had the same defect. Is the difference between the not proportions significant ?

Ans. The difference in proportions is not significant at 5% level.

2. In two large populations there are 30% and 25% fair haired people. Is this difference likely to be hidden in the samples of 1200 and 900 respectively drawn from the populations ?

Ans. The samples do not reveal the difference in the population proportions at 1% level

3. In a town A there were 956 births of which 52.5% was male. It another town B there were 450 births and the percentage of males in the total births of A and B was 49.6. Is the difference in the proportion of A and B significant?

Ans. The difference in the sample proportions is significant at 1% level

4. An examining body claims that among those who passed, the girls are 8% more than the boys. But in a sample of 200 examinees there are 42 girls who passed and in another sample of 100 examinees there are 18 boys who passed. Test whether the claim can be accepted or not.

Ans. The claim can be accepted at 5% level of significance.

5. In a random sample of 800 adults from the population of a certain large city, 600 are found to have dark hair. In a random sample of 1000 adults from the habitants of another large city 700 are dark haired. Show that the difference of the proportion of dark haired people is nearly 2.4 times the standard error of the difference of above sizes.

6. In a referendum submitted to the student body at a university. 850 men and 566 women voted. 530 of the men and 304 of the women voted yes. Does this indicate a significant difference of opinion on the matter at 1% level between men and women students.

Ans. the null hypothesis is rejected at 1% level of significance yes.

7. A machine puts out 16 imperfect articles in a sample of 500. After machine is overhauled it puts out 3 imperfect articles in a batch of 100. Has the machine improved?

Ans. The machine has not improved.

8. 1000 apples kept under one type of storage were found to show rotting is to the extent of 4%. 1500 apples kept under another kind of storage showed 3% rotting. Can it be reasonably concluded that the second type bad av avod loodoa 0001 of storage is superior to the first ?

Ans. There is no significant differences between the proportion oge of rotten apples in the two storages.