Maxwell's Equations

Maxwell's Equations

AU Dec.-02, 04, 05, 09, 13, 14 06, 07, 08, 10, 11, 12, 16, 17, 18, May-04, 05, 06, 10, 12, 14, 08, 11, 16, 17, 18

• We have previously studied that a static electric field   can exist without a magnetic field  demonstrated by a capacitor with a static charge Q. Similarly a conductor with a constant current I has a magnetic field  in the absence of an electric field  But in case of the time variable fields,  cannot exist without each other.

• The valuable work done by James Clerk Maxwell helped in discovering electromagnetic waves. The time varying fields are involved in the experiments of Faraday, Hertz and the theoretical analysis done by Maxwell.

• Maxwell's equations are nothing but a set of four expressions derived from Ampere's circuit law, Faraday's law, Gauss's law for electric field and Gauss's law for magnetic field. These four expressions can be written in following forms.

• Thus Maxwell's equations are nothing but the equations describing relationships between changing electric and magnetic fields. The Maxwell's equations in integral form govern the independence of fields like , along with soruces of fields like charge and current associated with different regions in the space like surfaces and volumes. On the other hand, the Maxwell's equations in point form or differential form explains the characteristics of different field vectors at a given point to each other as well as to the charge and current densities at that point.

• Basically the Maxwell’s equations are very important equations as they are found to be the basic mathematical background for the theory of an electromagnetic waves, transmission lines and also even study of antennas. Thus the applications of the electromagnetic fields can be verywell studied with the help of Maxwell's equations.

• Let us now discuss Maxwell's equations for static fields first and then for time varying fields.

 

1. Maxwell's Equations for Static Fields

• The basic Maxwell's equations for static fields are derived from Faraday's law, Ampere circuit law, Gauss's law for electrostatic field and Gauss's law for magnetostatic field.

A] Maxwell's Equation Derived from Faraday's Law

• According to the basic concept from an electrostatic field, the work done over a closed path or closed contour (i.e. starting point same as terminating point) is always zero. Mathematically it is represented as,

• The equation (9.5.1 (a)) is called integral form of Maxwell's equation derived from Faraday's law for static field.

• Now using Stake's theorem converting the closed line integral into the surface integral, we get,

• The equation (9.5.1 (b)) is called point or differential form of Maxwell's equation derived from Faraday's law for static fields.

B] Maxwell's Equation Derived from Ampere's Circuit Law

• According to basic concept from magnetostatics an Ampere's circuital law states that the line integral of magnetic field intensity  around a closed path is exactly equal to the direct current enclosed by that path. Mathematically it is given as,

• The integral in above expression should be current enclosed by the differential element. Now the current enclosed is equal to the product of current density normal to closed path and area of closed path. Hence we get,

• The equation (9.5.2 (a)) is called integral form of Maxwell's equation derived from Ampere's circuit law for static field.

• Now to relate , converting closed line integral on L.H.S. of the equation (9.5.2 (a)) to surface integral using Stake's theorem, we get

• The equation (9.5.2 (b)) is called point or differential form of Maxwell's equation derived from Ampere's circuit law for static field.

C] Maxwell's Equation Derived from Gauss's Law for Electrostatic Fields

• According to Gauss's law for electrostatic field, the electric flux passing through any closed surface is equal to the total charge enclosed by that surface. Mathematically we can write,

• The most common form to represent Gauss's law mathematically is with volume charge density ρv. Hence we can write,

• The equation (9.5.3 (a)) is called integral form of Maxwell's equation derived from Gauss's law for static electric field.

• To establish relationship between  and ρv, converting closed surface integral into volume integral using Divergence theorem as,

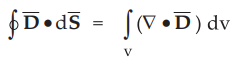
• Comparing above equation with equation (9.5.3 (a)), we can write,

• The equation (9.5.3 (b)) is called point or differential form of Maxwell's equation derived from Gauss's law for static electric field.

D] Maxwell's Equation Derived from Gauss's Law for Magnetostatic Field

• According to the Gauss's law for the magnetostatic field, the magnetic flux cannot reside in a closed surface due to the non existance of single magnetic pole.

• Mathematically we can write,

• The equation (9.5.4 (a)) is called integral form of Maxwell's equation derived from Gauss's law for static magnetic field.

• Now using divergence theorem, we can write,

 

• The equation (9.5.4 (b)) is called point or differential form of Maxwell's equation derived from Gauss's law for static magnetic field.

 

2. Maxwell's Equations for Time Varying Fields

• Similar to the static fields, the Maxwell's equations for the time varying fields are derived from Faraday's law, Ampere's circuit law, Gauss's law for electric field and Gauss's law for magnetic field.

A] Maxwell's Equation Derived from Faraday's Law

• Now consider Faraday's law which relates e.m.f. induced in a circuit to the time rate of decrease of total magnetic flux linking the circuit. In general we can write,

• This is Maxwell's equation derived from Faraday's law expressed in integral form.

Statement : "The total electromotive force (e.m.f.) induced in a closed path is equal to the negative surface integral of the rate of change of flux density with respect to time over an entire surface bounded by the same closed path."

• Using Stake's theorem, converting line integral of equation (9.5.5) to the surface integral,

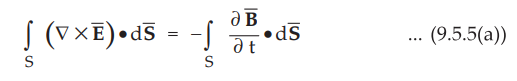
• Assuming that the integration is carried out over the same surface on both the sides, we get,

• This is Maxwell's equation derived from Faraday's law expressed in point form or differential form.

B] Maxwell's Equation Derived from Ampere's Circuit Law

• According to Ampere's circuit law, the line integral of magnetic field intensity  around a closed path is equal to the current enclosed by the path.

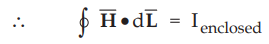
• Replacing current by the surface integral of conduction current density  over an area bounded by the path of integration of , we get more general relation as,

• Above expression Scan be made further general by adding displacement current density to conduction current density as follows,

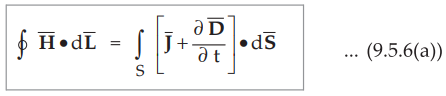
• Equation (9.5.6(a)) is Maxwell's equation derived from Ampere's circuit law. This equation is in integral form in which line integral of  is carried over the closed path bounding the surface S over which the integration is carried out on R.H.S. In the circuit theory, closed path is called Mesh. Hence the equation considered above is also called Mesh equation or Mesh relation.

Statement : "The total magnetomotive force around any closed path is equal to the surface integral of the conduction and displacement current densities over the entire surface bounded by the same closed path."

• Applying Stake's theorem to L.H.S. of the equation (9.5.6(a)), we get,

• Assuming that the surface considered for both the integrations is same, we can write,

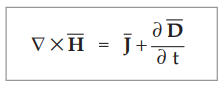... (9.5.6(b))

• Above equation is the Point form or differential form of Maxwell's equation derived from Ampere's circuit law.

C] Maxwell's Equation Derived from Gauss's Law for Electric Field

• According to Gauss's law, the total flux out of the closed surface is equal to the net charge within the surface. This can be written in integral form as,

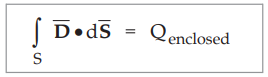 ... (9.5.7)

• If we replace R.H.S. of above equation by the volume integral of volume charge density ρ v through the volume enclosed by the surface S considered for integration at L.H.S. of equation (9.5.7), we get more general form of equation given by

... (9.5.7(a))

• This equation is called Maxwell's equation for electric fields derived from Gauss's law, expressed in integral form and applied to a finite volume.

Statement : "The total flux leaving out of a closed surface is equal to the total charge enclosed by a finite volume."

• Using divergence theorem, we can write

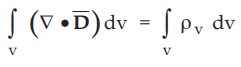
• Assuming same volume for integration on both the sides,

... (9.5.7(b))

• This is Maxwell's equation for electric fields derived from Gauss's law which is expressed in point form or differential form.

D] Maxwell's Equation Derived from Gauss's Law Magnetic Fields

• For magnetic fields, the surface integral of   over a closed surface S is always zero, due to non existence of monopole in the magnetic fields.

• This is Maxwell's magnetic field equation expressed in integral form. This is derived for Gauss's law applied to the magnetic fields.

Statement : "The surface integral of magnetic flux density over a closed surface is always equal to zero."

Using divergence theorem, the surface integral can be converted to volume integral as,

• This is differential form or point form of Maxwell's Equations derived from Gauss’s law applied to the magnectic fields.

Table 9.5.1 summarizes Maxwell’s equations

a. Maxwell's Equations for Free Space

• In the previous section, we have obtained Maxwell's equations in integral and point form. Let us consider now free space as a medium in which fields are present. Free space is a non-conducting medium in which volume charge density ρv is zero and conductivity σ is also zero.

• The Maxwell's equation, in the free space are as mentioned below.

b. Maxwell's Equations for Good Conductor

• It is clear from the type of the medium, that the conductivity is very high. So for good conductors we can write,

• The Maxwell's equations for good conductor medium are as follows.

c. Maxwell's Equations for Harmonically Varying Filds

• Let us assume that the electric and magnetic fields are varying harmonically with time. The electric flux density can be written as,

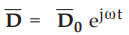
• Similarly the magnetic flux density can be written as,

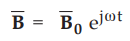
• Taking partial derivative with respect to time, we can write,

 

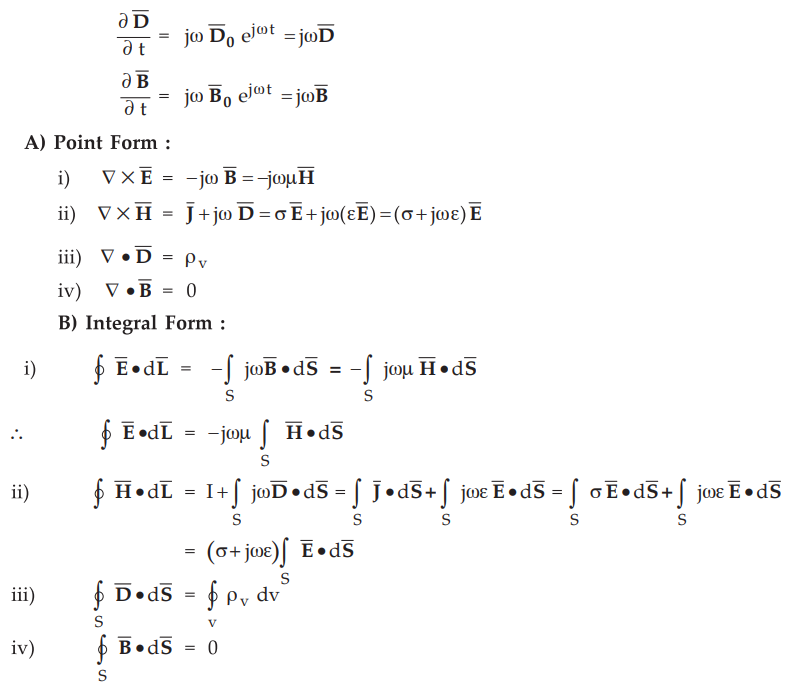
Ex. 9.5.1 If , Find the value of k to satisfy the Maxwell's equations for region σ = 0, ρv = 0.

Sol. : As σ  = 0 and ρv = 0, the medium in which  are present is nothing but free space. So the Maxwell's equation obtained from Gauss's law is given by,

 

Ex. 9.5.2 A certain material has σ  =0 and µr =1 If  making use of Maxwell's equations, find Ɛ_r and 

Sol. :

 

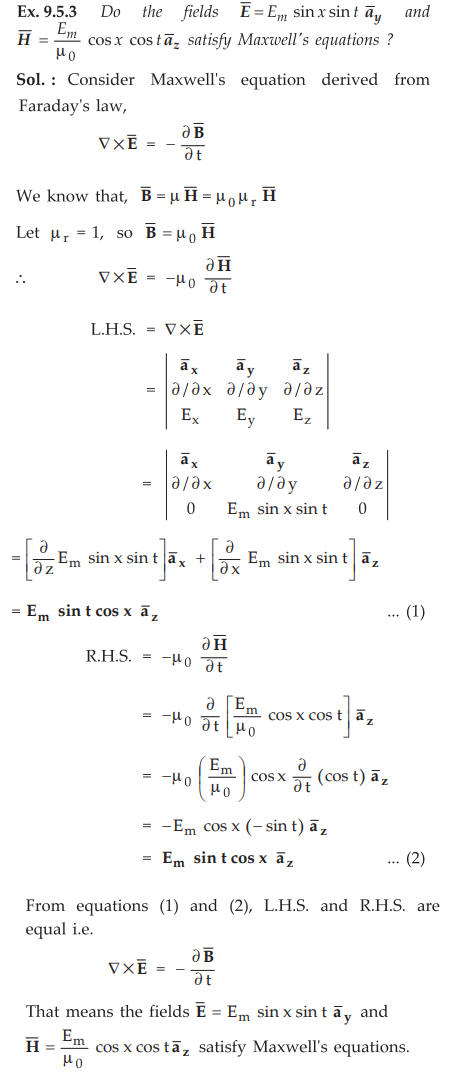
Ex. 9.5.4 The magnetic field intensity in free space is given as  is constant. Determine the current density vector  .

AU : Dec.-09, Marks 6

Sol. : According to Maxwell’s second equation for free space in the point form,

Examples for Practices

Ex. 9.5.7 In the charge free region, the magnetic field intensity is given by :

Ex. 9.5.8 Let µ = 10^-5H/m. Ɛ = 4 × 10-9 F / m. σ = 0, ρv = 0.

Find K (including units) so that each of the following pairs of field satisfies Maxwell's equations :

Ex. 9.5.9 A certain material has σ = 0, µr = 1.

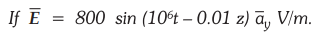 Make a use of Maxwell’s equation to find Ɛ_r = 8.9877

Ans . : 8.9877

Review Questions

1. Derive and explain Maxwell's equations both in integral and point forms.

AU : May-06, 10,16, 17, 18, Dec.-09, 10, 06, 05, 07, 08, 17, 13, 16, Marks 16; Dec.-14, 18, Marks 10

2. Derive the Maxwell's equations for fields varying harmonically with time.

AU : May-04, Marks 3, Dec.-12, 13, Marks 16

3. Derive Maxwell's equation in point form and integral form using Ampere's law, Faraday's law and Gauss law.

AU : May-11, 12, 14, Dec.-04, Marks 16

4. State and explain Maxwell's equations and give their physical significances.

AU : May-05, Dec.-02, 06, Marks 10