Minimization of POS Expressions

Minimization of POS Expressions

AU : May-04, 15

• In the above discussion, we have considered the Boolean expression in sum of products form and grouped 2, 4, and 8 adjacent ones to get the simplified Boolean expression in the same form. In practice, the designer should examine both the sum of products and product of stuns reductions to ascertain which is more simplified. We have already seen the representation of product of sums on the Karnaugh map. Once the expression is plotted on the K-map instead of making the groups of ones, we have to make groups of zeros. Each group of zero results a sum term and it is nothing but the prime implicate. The technique for using maps for POS reductions is a simple step by step process and it is similar to the one used earlier.

1. Plot the K-map and place 0s in those cells corresponding to the 0s in the truth table or maxterms in the product of sums expression.

2. Check the K-map for adjacent 0s and encircle those 0s which are not adjacent to any other 0s. These are called isolated 0s.

3. Check for those 0s which are adjacent to only one other 0s and encircle such pairs.

4. Check for quads and octets of adjacent 0s even if it contains some 0s that have already been encircled. While doing this make sure that there are minimum number of groups.

5. Combine any pairs necessary to include any 0s that have not yet been grouped.

6. Form the simplified POS expression for F by taking product of sum terms of all the groups.

To get familiar with these steps we will solve some examples.

Examples for Understanding

Ex. 3.5.1 Minimize the expression.

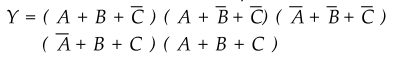
Sol. :

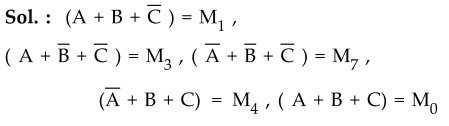
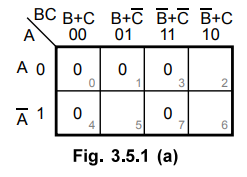
Step 1 : Fig. 3.5.1 (a) shows the K-map for three variable and it is plotted according to given maxterms.

Step 2 : There are no isolated 0s. 

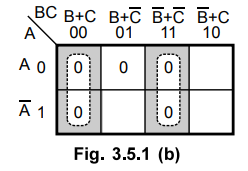
Step 3 : 0 in the cell 4 is adjacent only to 0 in the cell 0 and 0 in the cell 7 is adjacent only to 0 in the cell 3. These two pairs are combined and referred to as group 1 and group 2 respectively.

Step 4 : There are no quads and octets.

Step 5 : The 0 in the cell 1 can be combined with 0 in the cell 3 to form a pair. This pair is referred to as group 3.

Step 6 : jn group 1 and in group 2, A is eliminated, whereas in group 3 variable B is eliminated and we get,

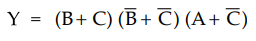
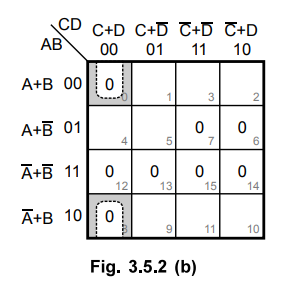
Ex. 3.5.2 Minimize the following expression in the POS form

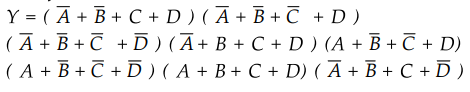
Sol. :

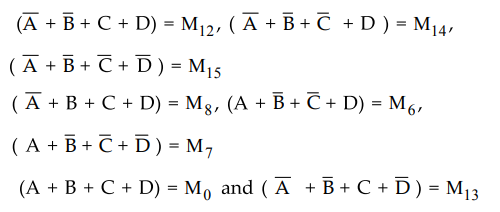
Step 1 : Fig. 3.5.2 (a) shows the K-map for four variable and it is plotted according to given maxterms.

Step 2 : There are no isolated 0s.

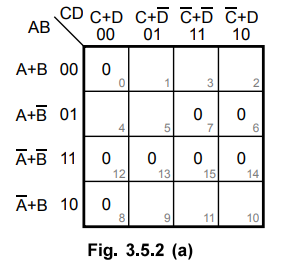
Step 3 : 0 in the cell 0 is adjacent only to 0 in the cell 8. This pair is combined and referred to as group 1.

Step 4 : There are two quads. Cells 12, 13, 14 and 15 forms a quad 1 and cells 6, 7, 14, 15 forms a quad 2. These two quads are referred to as group 2 and group 3, respectively.

Step 5 : All Os have already been grouped.

Step 6 : In group 1, variable A is eliminated. In group 2, variable C and D are eliminated and in group 3 variables A and D are eliminated. Therefore we get simplified POS expression as,

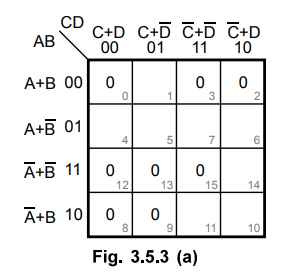
Ex. 3.5.3 Reduce the following function using K-map technique

f(A,B,C,D) = II M(0,2, 3, 8, 9, 12, 13, 15)

AU : May-15, Marks 8

Sol. :

Step 1 : Fig. 3.5.3 (a) shows the K-map for four variables and it is plotted according to given maxterms.

Step 2 : There are no isolated 0s.

Step 3 : The 0 in the cell 15 is adjacent only to 0 in the cell 13 and 0 in the cell 3 is adjacent only to 0 in the cell 2. These two pairs are combined and referred to as group 1 and group 2, respectively.

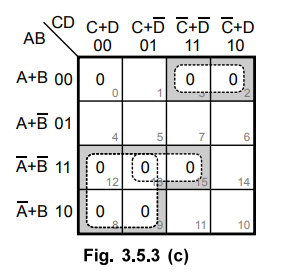
Step 4 : The cells 8, 9, 12 and 13 form a quad which is referred to as group 3.

Step 5 : The remaining 0 in the cell 0 is combined with the 0 in the cell 2 to form a pair, which is referred to as group 4.

Step 6 : In group 1 and in group 4 variable C is eliminated. In group 2 variable D is eliminated and in group 3 variables B and D are eliminated. Therefore, we get simplified expression in POS form as,

Examples with Solutions

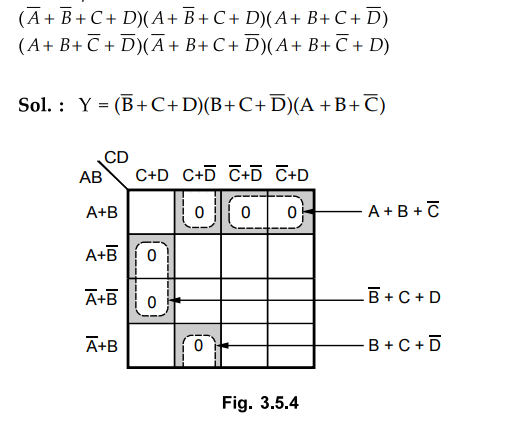
Ex. 3.5.4 Simplify using K-map to obtain a minimum POS expression :

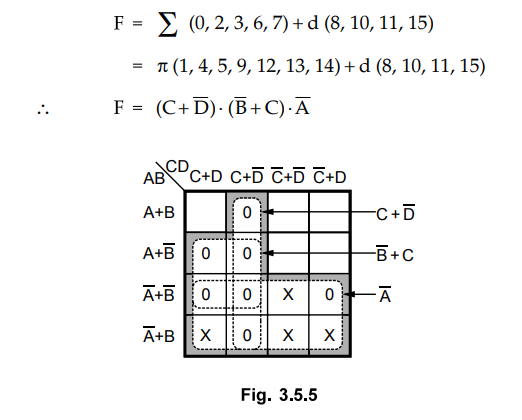
Ex. 3.5.5 Obtain the minimal product of sums for

F = ∑ (0, 2, 3, 6,7) + d (8,10, 11,15)

Sol. :

Examples for Practice

Ex. 3.5.6 Simplify the following Boolean function for minimal POS form

Ex. 3.5.7 Reduce the following function using K-map n

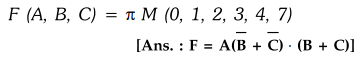
Review Question

1. Give the steps for simplification of POS expression.