Minimization of SOP Expressions

Minimization of SOP Expressions

AU : Dec.-03, 05, 17, May-05, 06, 10, 13

• We have seen how combination of pairs, quads and octets on a Karnaugh map can be used to obtain a simplified expression. A pair of Is eliminates one variable, a quad of Is eliminates two variables and an octet of Is eliminates three variables. In general, when a variable appears in both complemented and uncomplemented form within a group, that variable is eliminated from the resultant expression. Variables that are same in all with the group must appear in the final expression. Each group gives us a product term and summation of all product term gives us a Boolean expression. Therefore, we can say that, each product term implies the function and, hence is an implicant of the function. All the implicants of a function determined using a Karnaugh map are the prime implicants.

From the above discussion we can outline generalized procedure to simplify Boolean expressions as follows :

1. Plot the K-map and place Is in those cells corresponding to the Is in the truth table or sum of product expression. Place Os in other cells.

2. Check the K-map for adjacent Is and encircle those Is which are not adjacent to any other Is. These are called isolated Is.

3. Check for those Is which are adjacent to only one other 1 and encircle such pairs.

4. Check for quads and octets of adjacent Is even if it contains some Is that have already been encircled. While doing this make sure that there are minimum number of groups. 

5. Combine any pairs necessary to include any Is that have not yet been grouped.

6. Form the simplified expression by summing product terms of all the groups.

 

Examples for Understanding

Ex. 3.4.1 Minimize the expression

Sol. :

Step 1 : Fig 3.4.1 (a) shows the K-map for three variables and it is plotted according to the given expression.

Step 2 : There are no isolated 1s.

Step 3 : 1 in the cell 3 is adjacent only to 1 in the cell 1. This pair is combined and referred to as group 1.

Step 4: There is no octet, but there is a quad. Cells 0, 1, 4 and 5 form a quad. This quad is combined and referred to as group 2.

Step 5: All 1s have already been grouped.

Step 6 :  Each group generates a term in the expression for Y. In group 1 B variable is eliminated and in group 2 variables A and C are eliminated and we get,

 

Ex. 3.4.2 Minimize the expression

Sol. :

Step 1 : Fig. 3.4.2 (a) shows the K-map for four variables and it is plotted according to the given expression.

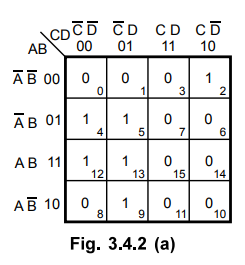
Step 2 : Cell 2 is the only cell containing a 1 that is not adjacent to any other 1. It is referred to separately as group 1.

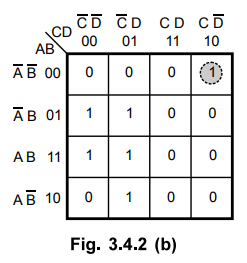
Step 3 : 1 in the cell 9 is adjacent only to 1 in the cell 13. This pair is combined and referred to as group 2.

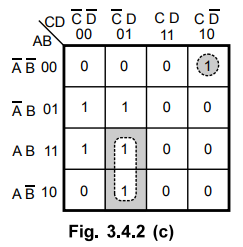
Step 4 : There is no octet, but there is quad cells 4, 5, 12 and 13 form a quad. This quad is combined and referred to as group 3.

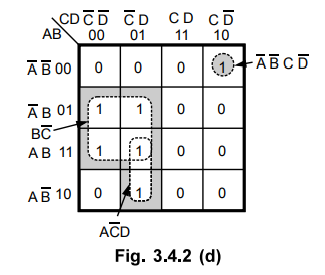
Step 5 : All Is have already grouped.

Step 6 : Each group generates a term         in the expression for Y. In group 1 variable is not eliminated. In group 2 variable B is eliminated and in group 3 variables A and D are eliminated and we get,

 

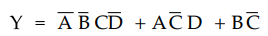
Ex. 3.4.3 Reduce the following four variable function to its minimum sum of products form :

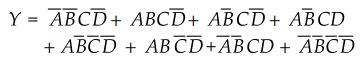
Sol. :

Step 1 : Fig. 3.4.3 (a) shows the K-map for four variables and it is plotted according to the given expression.

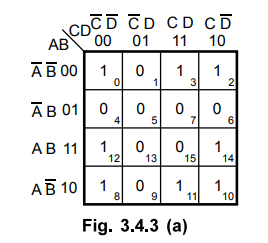
Step 2 : There are no isolated Is.

Step 3 : There are no such Is which are adjacent to only one other 1.

Step 4 : There are three quads formed by cells 0, 2, 8, 10, cells 8, 10, 12, 14 and cells 2, 3, 10, 11. These quads are combined and referred to as group 1, group 2 and group 3 respectively.

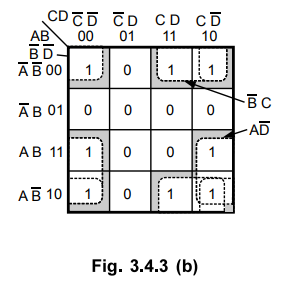
Step 5 : All 1s have already been grouped.

Step 6 : Each group generates a term in the expression for Y. In group 1 variables A and C are eliminated, in group 2 variables B and C are eliminated and in group 3 variables A and D are eliminated and we get,

 

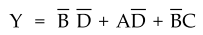
Ex. 3.4.4 Reduce the following function to its minimum sum of products form :

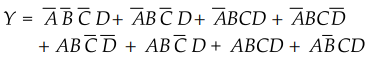
Sol. :

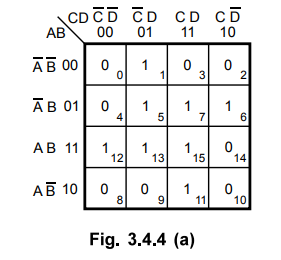
Step 1 : Fig. 3.4.4 (a) shows the K-map for four variables and it is plotted according to the given expression.

Step 2 : There are no isolated Is.

Step 3 : The 1 in the cell 1 is adjacent only to 1 in the cell 5, the 1 in the cell 6 is adjacent only to the 1 in the cell 7, the 1 in the cell 12 is adjacent only to the 1 in the cell 13 and the 1 in the cell 11 is adjacent only to the 1 in the cell 15. These pairs are combined and referred to as group 1-4 respectively.

Step 4 : There is no octet, but there is a quad. However, all Is in the quad have already been grouped. Therefore this quad is ignored.

Step 5 : All Is have already been grouped.

Step 6 : Each group generates a term in the expression for Y. In group 1 variable B is eliminated. Similarly, in group 2-4 variables D, D and B are eliminated one in each group. We finally get minimum sum of products form as,

 

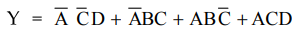
Ex. 3.4.5 Simplify the logic function specified by the truth Table 3.4.1 using the Karnaugh map method. Y is the output variable, and A, B and C are the input variables.

Sol. :

Step 1 : Fig. 3.4.5 (a) shows the K-map for three variables and it is plotted according to given truth table.

Step 2 : There are no isolated 1s.

Step 3 : The 1 in the cell 0 is adjacent only to 1 in the cell 4 and the 1 in the cell 3 is adjacent only to 1 in the cell 7. These two pairs are grouped and referred to as group 1 and group 2.

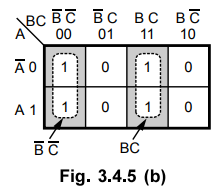
Step 4 : There is no octet and quad.

Step 5 : All Is have already been grouped.

Step 6 : In group 1 and group 2 variable A is eliminated and we get,

 

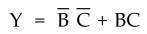
Ex. 3.4.6 Reduce the following function using Karnaugh map technique and implement using basic gates

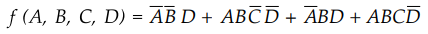
Sol. : The given function is not in the standard sum of products form. It is converted into standard SOP form as given below.

Step 1 : Fig. 3.4.6 (a) shows the K-map for four variables and it is plotted according to expression in standard SOP form.

Step 2: There are no isolated 1s

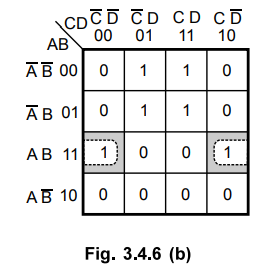
Step 3 : The 1 in the cell 12 is adjacent only to the 1 in the cell 14. This pair is combined and referred to as group 1.

Step 4 : There is a quad. Cells 1, 3, 5 and 7 form a quad. This quad is referred to as group 2.

Step 5 : All Is have already been grouped.

Step 6 : In group 1 variable C is eliminated and in group 2 variables B and C are eliminated. We get simplified equation as,

 

Ex. 3.4.7 Reduce the following function using K-map technique.

f ( A, B, C, D) = ∑ m (0, 1, 4, 8, 9, 10).

Sol. :

Step 1 : Fig. 3.4.7 (a) shows the K-map for four variables and it is plotted according to given minterms.

Step 2 : There are no isolated 1s.

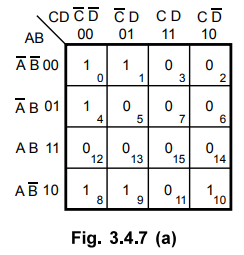
 Step 3 : Cell 4 is adjacent only to cell 0 and cell 10 is adjacent only to cell 8. These two pairs are combined and referred to as group 1 and group 2 respectively.

Step 4 : There is a quad. Cells 0, 1, 8 and 9 form a quad. This quad is referred to as group 3.

Step 5 : All Is have already been grouped.

Step 6 : In group 1, B and in group 2, C are eliminated respectively. In group 3, A and D are eliminated and finally we get

 

Examples with Solutions

Ex. 3.4.8 Plot the following Boolean function on a Karnaugh map and simplify it.

F(w, x, y, z) = ∑ ( 0,1,2,4,5,6,8,9,12,13,14)

AU ; Dec.-05, May-10, Marks 6

Sol. :

 

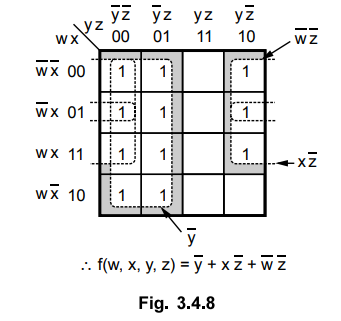
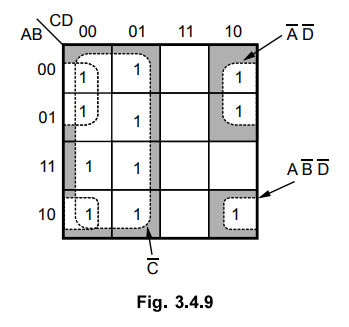
Ex. 3. 4. 9. Show the Karnaugh groups for the Boolean function,

Sol. :

 

Examples for Practice

Ex. 3.4.10 Simplify following logical expression using Karnaugh maps

Ex. 3.4.11 Simplify the following function

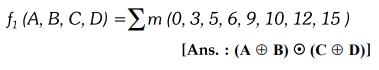
Ex 3.4.12 Simplify the following function

 

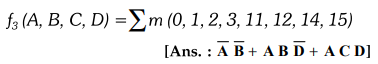
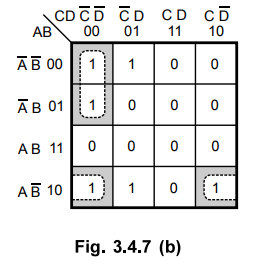
1. Essential Prime Implicants

• After grouping the cells, the sum terms which appear in the K-map are called prime implicants groups. It is observed that some cells may appear in only one prime implicants group; while other cells may appear in more than one prime implicants group. In Fig. 3.4.7 (c), cells 1, 4, 9 and 10 appear in only one prime implicants group. These cells are called essential cells and corresponding prime implicants are called essential prime implicants.

 

2. Incompletely Specified Functions (Don't Care Terms)

• In some logic circuits, certain input conditions never occur, therefore the corresponding output never appears. In such cases the output level is not defined, it can be either HIGH or LOW. These output levels are indicated by 'X' or'd' in the truth tables and are called don't care outputs or don't care conditions or incompletely specified functions. Let us see the output levels in the truth table as shown in the Table 3.4.2. Here outputs are defined for input conditions from 0 0 0 to 1 0 1. For remaining two conditions of input, output is not defined, hence these are called don't care conditions for this truth table.

• A circuit designer is free to make the output for any "don't care" condition either a '0' or a '1' in order to produce the simplest output expression.

a. Describing Incomplete Boolean Function

• We know that we describe the Boolean function using either a minterm canonical formula or a maxterm canonical formula. In order to obtain similar-type expressions for incomplete Boolean functions we use additional term to specify don't care conditions in the original expression. This is illustrated in the following examples.

• In expression,

f(A, B, C) = ∑ m (0, 2, 4) + d (1, 5)

• minterms are 0, 2 and 4. The additional term d(l, 5) is introduced to specify the don't care conditions. This terms specifies that outputs for minterms 1 and 5 are not specified and hence these are don't care conditions. Letter d is used to indicate don't care conditions in the expression.

• The above expression indicates how to represent don't care conditions in the minterm canonical formula. In the similar manner, we can specify the don't care conditions in the maxterm canonical formula. For example,

f(A, B, C) = II M (2, 5, 7) + d(l, 3)

b. Don't Care Conditions in Logic Design

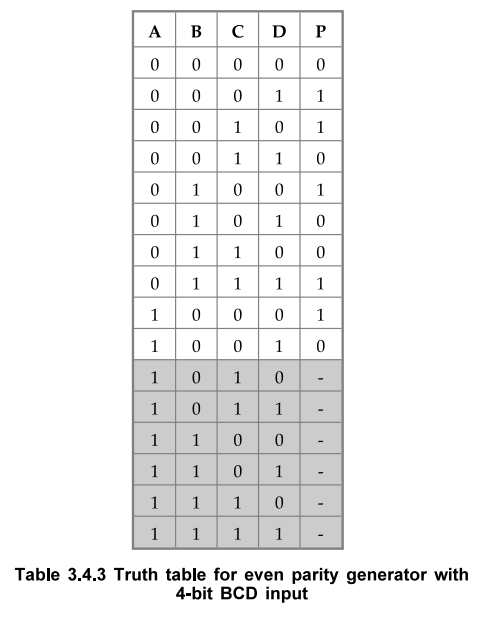
• In this section, we see the example of incompletely specified Boolean function. Let us see the logic circuit for an even parity generator for 4-bit BCD number. The Table 3.4.3 shows the truth table for even-parity generator. The truth table shows that the output for last six input conditions cannot be specified, because such input conditions does not occur when input is in the BCD form.

• The Boolean function for even parity generator with 4-bit BCD input can be expressed in minterm canonical formula as,

f(A, B, C) = ∑ m (1, 2, 4, 7, 8) + d (10, 11, 12, 13, 14, 15)

c. Minimization of Incompletely Specified Functions

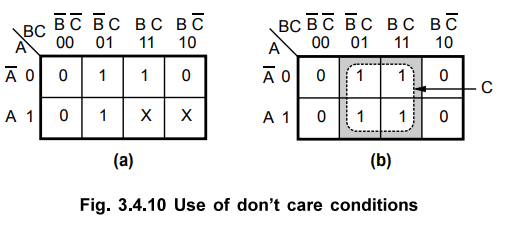
• A circuit designer is free to make the output for any don't care condition either a '0' or 1 in order to produce the simplest output expression. Consider a truth table shown in Table 3.4.4. The K-map for this trth table is shown in Fig. 3.4.10 with x placed in the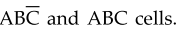 

• It is not always advisable to put don't cares as 1s. This is illustrated in Fig. 3.4.10 (b). Here, the don't care output for cell ABC is taken as 1 to form a quad and don't care output for cell  is taken as 0, since it is not helping any way to reduce an expression.

• Using don't care conditions in this way we get the simplified Boolean expression as

Y = C

• From the above discussion we can realize that it is important to decide which don't cares to change to 0 and which to 1 to produce the best K-map grouping (i.e. the simplest expression). Now, we will see more examples to provide practice in dealing with "don't care" conditions.

 

Examples for Understanding

Ex. 3.4.13 Find the reduced SOP from of the following function.

f(A, B, C, D) = ∑ m (1, 3, 7, 11, 15) + ∑d (0, 2, 4)

Sol. :

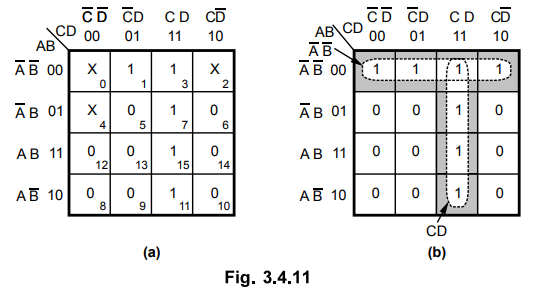
To form a quad of cells 0, 1, 2 and 3 the don't care conditions 0 and 2 are replaced by 1s.

The remaining don't care condition is replaced by 0 since it is not required to form any group. With these replacements we get the simplified equation as

 

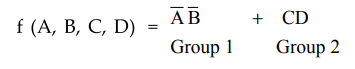
Ex. 3.4.14 Reduce the following function using Karnaugh map technique.

f  (A, B, C, D) = ∑m (5, 6, 7, 12, 13) + ∑ d (4, 9, 14, 15)

Sol. :

To form a octet of cells 4, 5, 6, 7, 12, 13, 14 and 15 the don't care conditions 4, 14 and 15 are replaced by Is. The remaining don't care condition 9 is replaced by 0 to get simplified function as,

f(A, B, C, D) = B

 

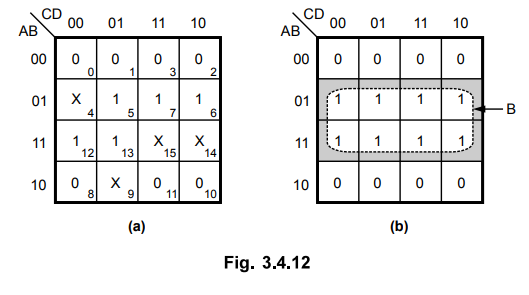
Ex. 3.4.15 Reduce the following function using Karnaugh map technique.

f(A, B, C) = ∑ m (0, 1, 3, 7) + ∑ d (2, 5)

Sol. :

To form two quads both the don't care conditions are replaced by Is and we get,

 

Examples with Solutions

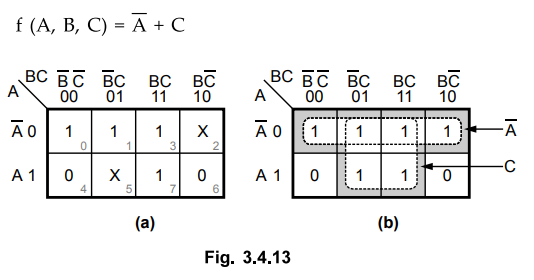
Ex. 3.4.16 Reduce the following function using Karnaugh map technique.

F (W, X, Y, Z) = ∑ m (0, 7, 8, 9, 10, 12) + ∑ d (2, 5, 13).

Sol. : In this example all don't cares are considered as 1s and we get,

 

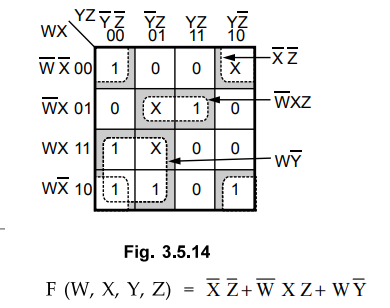
Ex. 3.4.17 Solve g (w, x, y, z) = ∑ m (1,3,4, 6,11) + ∑ d(0, 8,10,12,13)

AU : Hay-10, Harks 8

Sol. :

 

 

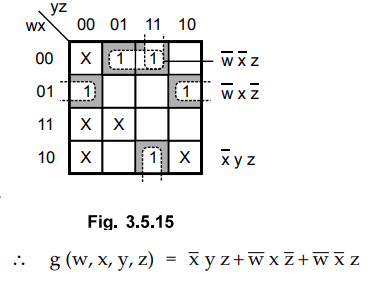
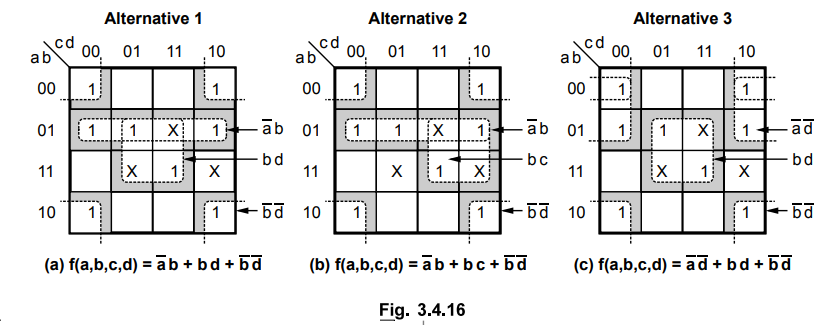
 Ex. 3.4.18 Express the following function as the minimal sum of products using a K-map. f(a,b,c,d) = S (0,2,4,5,6,8,10,15) + ∑ ϕ (7,13,14)

Sol. : As shown in Fig. 3.4.16 the given example has three solutions and all are correct. Students are expected to give any one solution.

 

Examples for Practice

Ex. 3.4.19 Simplify the following switching function using Karnaugh map

F(AB,C,D) = ∑ (0, 5, 7, 8, 9,10,11,14,15) + ϕ (1, 4,13).

 

Ex. 3.4.20 Simplify the Boolean function using K map

F(w, x, y, z) = ∑ (1, 3, 7,11,15) which has the don’t care conditions

d(w, x, y, z) = ∑ (0, 2, 5).

[Refer similar example 3.4.16. ]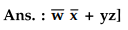

Review Questions

1. Give the steps for simplification of SOP expression.

2. What do you mean by essential prime implicants ?

3. What is don't care condition ?