Model Question Paper with Answer - 2 (PART B)

PART B-(5 × 16 = 80 MARKS)

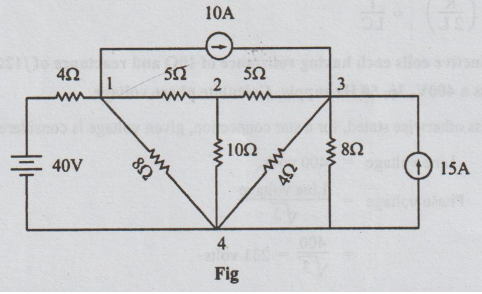
11. (a) (i) Use nodal voltage method and hence find the power dissipated in the 10 ohms resistor on the circuit shown in figure. (8)

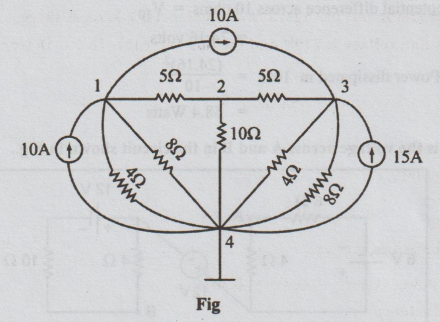
Solution: Taking the node 4 as reference, and converting the voltage source into current source, the above network is re-drawn as below:

The power dissipated in 10 Ω =( V₁₀)²/10 , (formula is power = V² /R)

V₁₀ = V₂ - V₄ =  V₂-0 = V₂

By inspection, we get

= -25 (0.575 × (-0.2)) = 2.875

V₂ = Δ₂/ Δ = 2.875/ 0.119 = 24.16 volts

Therefore, the potential difference across 10 ohms = V₁₀

=  24.16 volts

Power dissipated in 10 Ω = (24.16)²/10

= 58.4 Watts

 

11. (a) (ii) What is the voltage across A and B in the circuit shown in Fig..

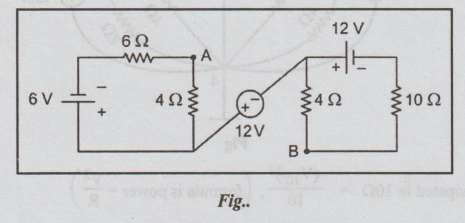
Solution:

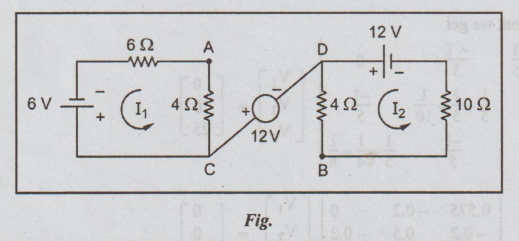
6V source drives current in left loop, 12 volt source drives current in right loop. There is no current flowing between C and D, as there is no closed path.

By Ohm's law, applied, we get

I₁ = 6 / 6 + 4  = 0.5 A

I₂ = 12 / 4 + 10 = 12/14 A

V_AB = V_AC + V_CD + V_DB

V_AB = I₁ (4) – 12 - I₂ (4)

= 0.5 (4) – 12 - 12

= -13.43 volts

= 13.43 volts with B at negative potential

 

(OR)

 

11.(b) (i) In the network shown in figure determine V2 such that the current in the 2 + j3 impedance is zero.

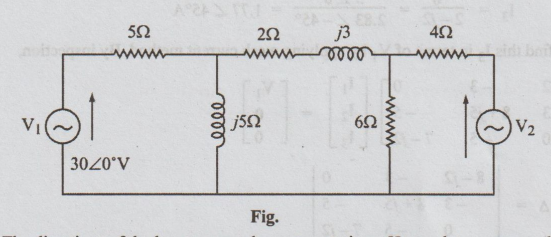
Solution: The directions of the loop currents here are not given. Hence, let us assume that they are all clockwise. Since the current through (2 + j3) is given to be zero, I₂ = 0 => Δ₂/ Δ = 0. Hence, the condition

Δ₂ = 0. So, by inspection

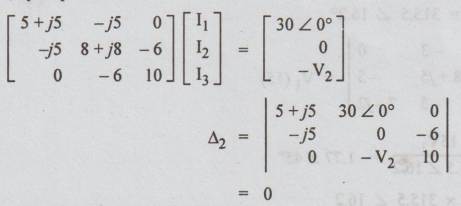
⇒ (5 + j5) (-6V₂)-30 ∠ 0° (-50 j) =  0

7.07 ∠  45 × (-6 V₂) = - 1500 ∠ 90°

 V2 = - 1500 ∠ 90° /  -42.42 ∠ 45°

= 35.36 ∠ 45°

 

11 (b) (ii) In the network shown in the figure the source V₁ results in a voltage V₀ across the (2 - j2)Ω impedance. Find the source V₁ which corresponds to V₀=50° volts. (8)

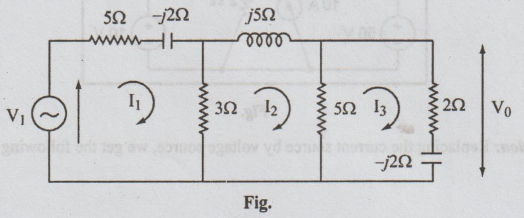
Solution: Let the loop currents be I₁, I₂ and I₃.

 

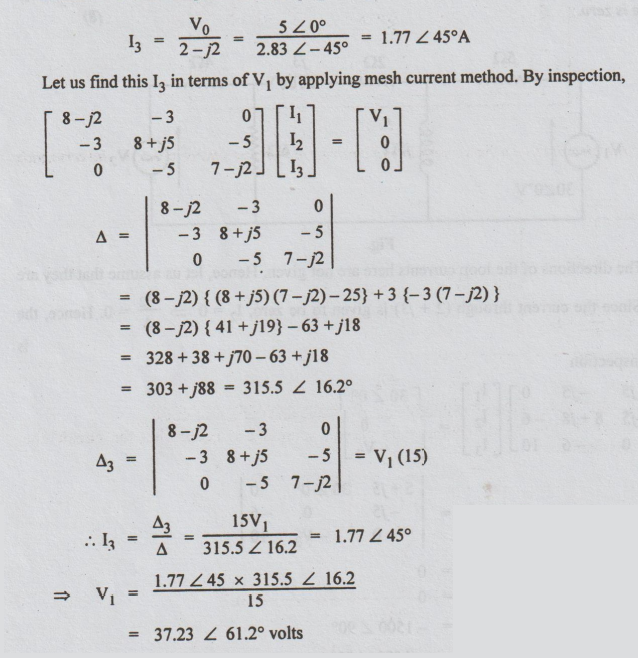
11. (b) Using source transformation, replace the current source in the circuit shown below by a voltage source and find the current delivered by the 50V voltage source. (8)

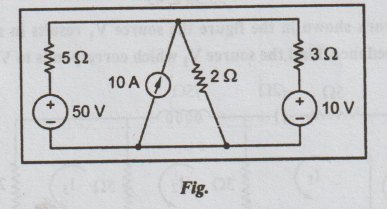
Solution: Replacing the current source by voltage source, we get the following circuit.

 

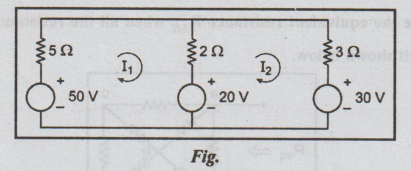
12. (a) (i) For the circuit shown below obtain the equivalent current source between the terminals

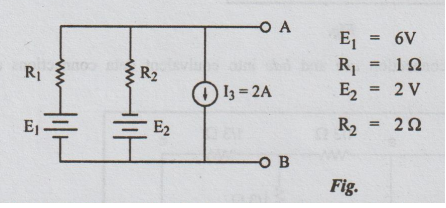
Solution: This problem is a parallel combination of voltage and current sources.

Step 1: Converting the voltage sources into current sources and re-drawing the circuit, the following figure is obtained.

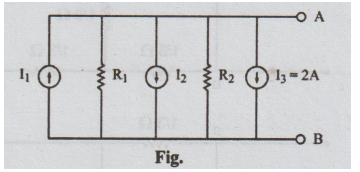
I₁ = 6/1 = 6A; R₁ =1 Ω; I₂ = 2/2 = 1A; R₂ =2 Ω

Step 2: The equivalent current source of the above circuit is as shown below:

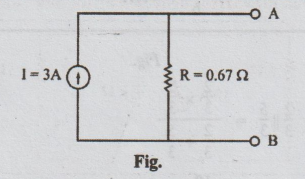
I = I₁ - I₂ - I₃ = 6-1-2 = 3A

R = R1|| R2 = R₁ R₂ / R₁ + R₂

= 1 × 2 / 1+2 = 2/3 = 0.67 Ω

 

12. (a) (ii) Calculate the equivalent resistance R_sh when all the resistance values are equal to 1Ω for the circuit shown below. (8)

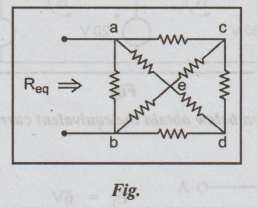
Solution: Converting star connection ace and bde into equivalent data connections and redrawing the circuit, we get

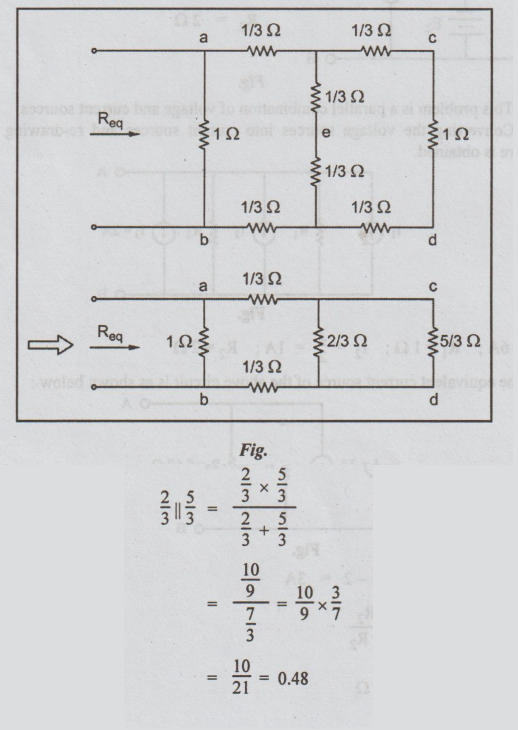
Then the circuit becomes

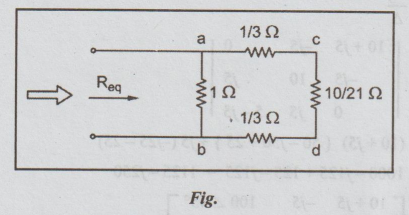
1/3 + 1/3 + 10/21 = 24/21 = 8/7

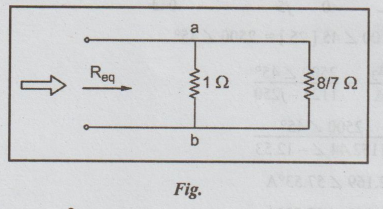
R_eq = R_ab = 1× 8/7 / 1 + 8/7 =  0.533 Ω

 

(OR)

 

12. (b) (i) In the network shown in the figure, the voltage source 100 ∠45°V causes current I_x in the 5.2 branch. Find Ix and then verify the reciprocity theorem for this circuit.

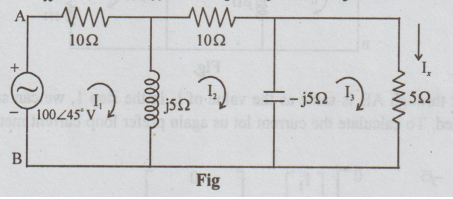
Solution: Step 1: It is required to find the value of I_x. Let us apply loop current method. If the loop currents are taken to be I₁, I₂ and I₃ as shown, then I_x = I₃.

For the above circuit, by inspection, we can write that

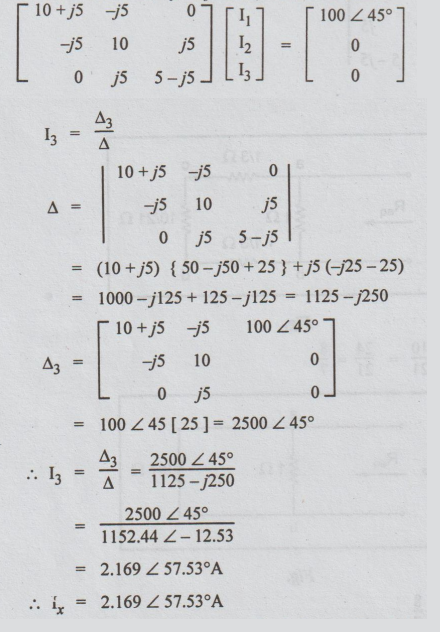
I₃ =Δ₃/Δ = 2500 ∠ 45° / 1125-j250

= 2500 ∠45^o / 1152.44 ∠ -12.53

= 2.169 ∠ 57.53°A

i_x= 2.169 ∠ 57. 53^o A

Step 2: Now connect the voltage source in the branch in which the current is I_x i.e., in 5Ω branch and connect an a.c. ammeter in the branch where the voltage source was connected earlier as shown below. If ammeter is not available, short the terminals A and B.

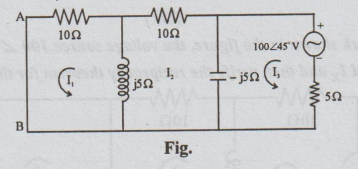
If the current through AB is same as the value of I_x in the step 1, we can say that the reciprocity theorem is verified. To calculate the current let us again prefer loop current method to other methods. By inspection.

I₁ = Δ₁/Δ = 2500 ∠ 45° / 1152.44 ∠ -12.53^o

=2.169 ∠ 57. 53^o A

I₁ = I_AB = I_x

Hence the reciprocity theorem is verified.

 

12. (b) (ii) Find the current through various branches of the circuit shown below, by employing superposition theorem. (8)

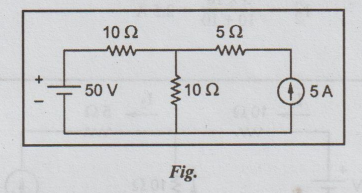
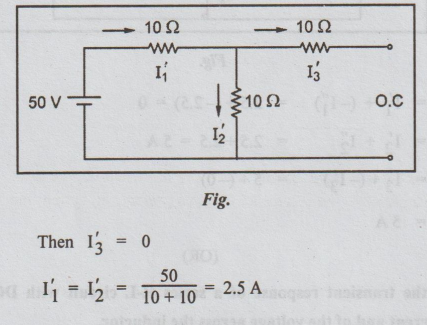
Step 1: Allow only voltage source to act. Open circuit the current source.

Step 2: Allow only current source to act. Short circuit the voltage source.

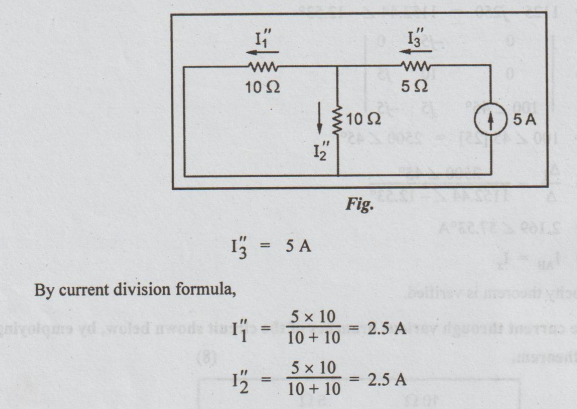
Step 3:

 

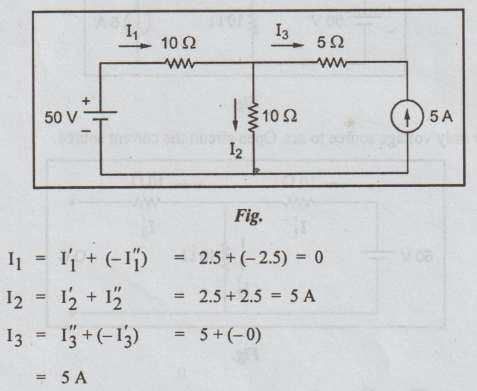
 (OR)

 

13. (a) (i) Derive the transient response of a series R-L circuit with DC input. Sketch the variation of current and of the voltage across the inductor.

(a) Case 1: (a) R-L Transients: (Rise of current) (16)

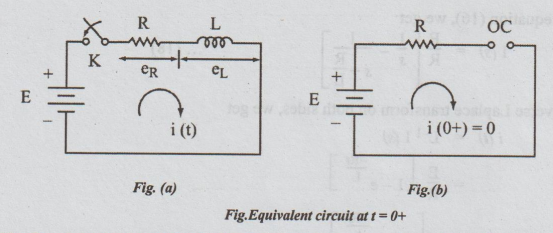
Let the R - L series combination be impressed upon the d.c. voltage E by closing the switch K. Assume that the current through the inductor before closing the switch is zero. Let K be closed at the instant t = 0.

The equivalent circuit at t = 0+ is shown in fig. The inductor is shown as open circuit. Hence i (0-) = i(0+) = 0.

Applying KVL to the circuit in fig. after t seconds of closing K,

we get, Ri+L di/dt =  E .....(15)

Taking Laplace Transformation on both sides, we get

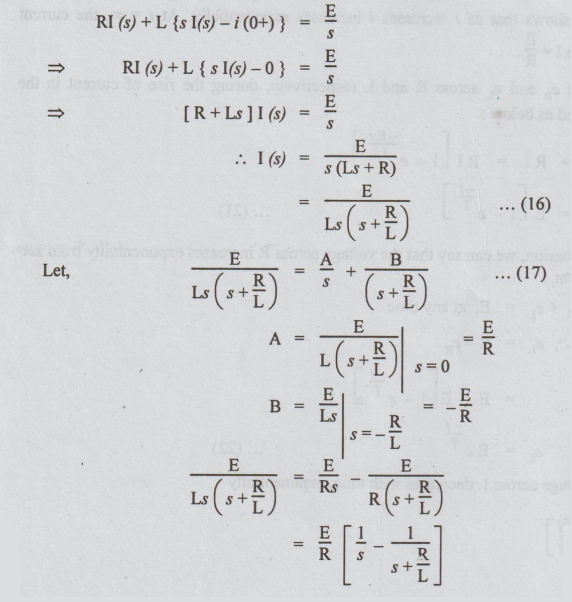
Steady current is the value of i(t) for t = ∞.

L/R is called time constant of the RL circuit and is denoted by T.

Hence equation (19) can be written as

I = 1 [1-e^-t/T]......... (20)

The above equation shows that as t increases i increases exponentially. At t = ∞, the current reaches steady state value I = E / R

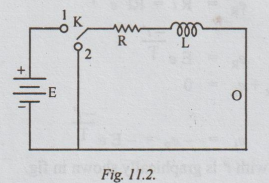
The transient voltage e_R and e_L across R and L respectively, during the rise of current in the inductive can be expressed as below:

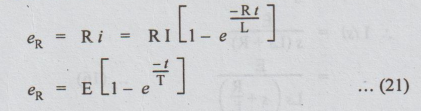
From the above expression, we can say that the voltage across R increases exponentially from zero to E, during rise of current.

By KVL, e_R + e_L = E, at any time

e_L = E - e_R

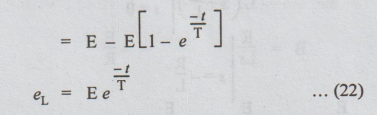
It shows that the voltage across L decreases with time, exponentially

[ Note: e_L = -L di / dt ]

The variation of i(t) with time is graphically shown in fig. and that of e, and e, is shown in fig. .

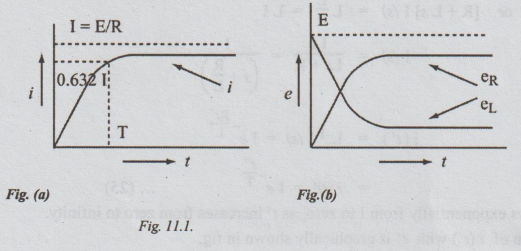
Definition of time constant T for RL circuit

Substituting T = t in equation (20), we get

i = I (1 - e^-1)

= 0.632 I

= 63.2% of I

Thus the time constant of RL series circuit is defined as the period during which the current rises to 63.2% of its final value (OR steady value).

(b) RL-Decaying Transients

Assume that the switch K is kept connected to position 1 for sufficiently longer period. Then the current reaches steady state value given by I = E / R After this instant, let the switch be moved from position 1 to position 2. Let this instant be taken as t’ = 0. After t' seconds of closing the switch to position, applying KVL,

Ri+ L  di / dt' = 0 ....(23)

Taking Laplace Transformation on both sides, we get

RI (s) + L [SI (s)-i (0+)] = 0 .....(24)

Here i (0+) = I = E / R

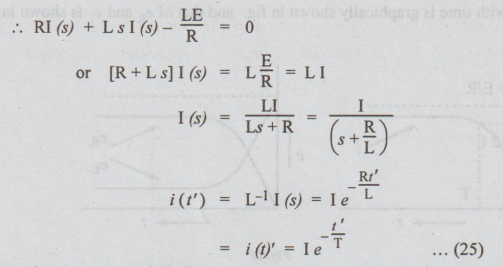
Thus i decays exponentially from I to zero, as t' increases from zero to infinity.

The variation of i (t') with t' is graphically shown in fig.

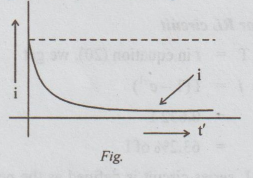
Decaying current in an R-L circuit.

e_R = Ri = RI e^-t/T

e_R = Ee^-t/T ....(26)

e_R + e_L = 0

 ⇒ e_L = -e_R = -Ee –^t/T …. (27)

The variatiom of e_R and e_L ith t’ is graphically shown in fig.

 

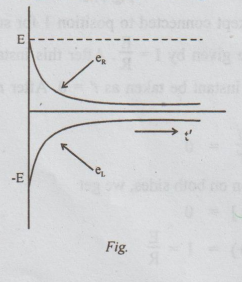
13. (b) Derive the expression for the complete solution of the current response of RC series circuit with an excitation of V cos (ωt + ϕ). Briefly explain the significance of phase angle in the solution. (16)

Solution:

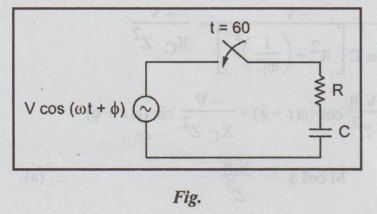
Apply KVL to get

Differentiating on both sides,

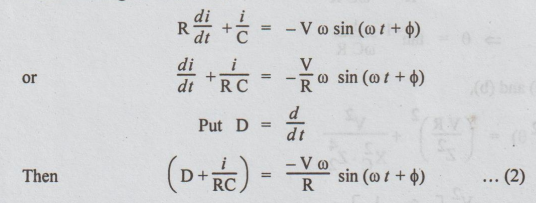
The complete solution consists of two parts. One is complementary and another is particular.

Complementary solution = iC = C e ^{- t/RC}....(3)

The particular solution, by using undetermined coefficients is

Ip = A cos (ωt + ϕ )+ B sin (ωt + ϕ)...(4)

Differentiating

 

14. (a) (i) A 3-phase balanced delta-connected load of (4+ j8) Ω is connected across a 400V, 3- phase supply. Determine the phase currents and line currents. Assume the RYB phase sequence. Also calculate the power drawn by the load. (16)

Solution:

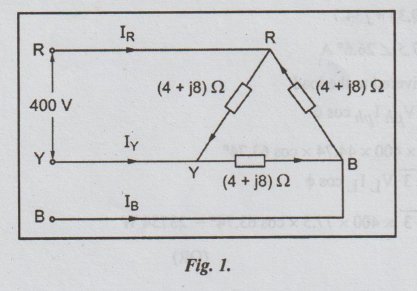
Z_RY = Z_YB = Z_BR=4+j8 = 8.94 ∠ 63.4°

V_RY = 400 ∠ 0°

V_YB = 400 ∠ -120°

V_BR  = 400 ∠ 120°

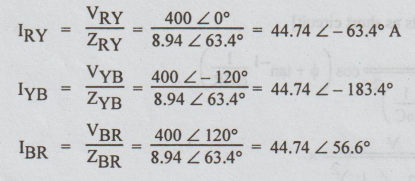
Line current (I_L):

I_R = I_RY - I_BR

= 44.74 ∠ -63.4° - 44.74 ∠ 56.6°

= (20.03 - j40) - (24.63 +j37.35)

= -4.6 - j77.35

= 77.5∠  -93.4°

I_Y = I_YB - I_RY

= 44.94 ∠ -183.4°- 44.74 ∠ -63.4°

= (-44.70+j2.65) - (20.03 -j40)

= -64.73 + j42.16

= 77.5 2146.6

I_B = I_BR - I_YB

= (24.63 + j37.35) - (-44.7 + j2.65)

= 69.33 + j34.7

= 77.5 ∠ 26.6° A

Total power delivered to the load

P = 3 V_ph I_ph cos ϕ

= 3 × 400 × 44.74 × cos 63.74°

or P = √3 VL I_L cos ϕ

= √3 × 400 × 77.5 × cos 63.74° = 23754 W

 

(OR)

 

14. (b) (i) If W1 and W2 are the readings of the two wattmeters which measure power in the three phase balanced system and if W₁/W₂ = a, show that the power factor of the circuit is given by cos ϕ = α + 1 / 2√ σ ² -  σ + 1 (8)

Solution:

W₁ = V_L I_L cos (30 + ϕ)

W₂ = V_L I_L cos (30 - ϕ)

W₁ + W₂ = V_L I_L cos (30 + ϕ) + V_L I_L cos (30 - ϕ)

= V_LI_L [2 cos 30°. cos ϕ]

= √3 V_L I_L Cos ϕ ....(1)

W₂ - W₁= V_L I_L cos (30 – ϕ ) - V_L I_L cos (30 + ϕ )

= V_LI_L [2 sin 30°. sin ϕ ]

W₂-W₁ = V_L I_L sin ϕ.....(2)

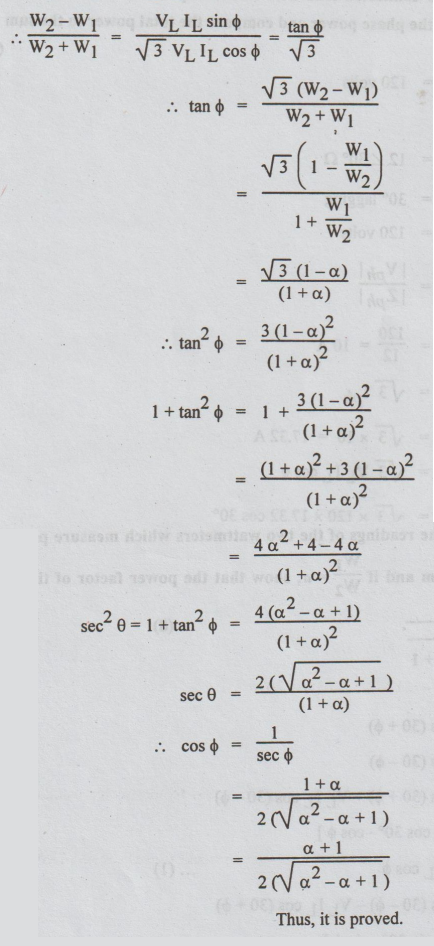
14. (b) (ii) Obtain the readings of two wattmeters connected to a three-phase three-wire 120V system feeding a balanced A-connected load with a load impedance of 12∠ 30° Ω. Assume either phase sequence. Find the phase power and compare the total power to the sum of the wattmeter readings. (8)

Solution:

V_L = 120 volts

Δ connected load:

Load impedance/phase = 12 ∠ 30° Ω

ϕ = 30° lagging

V_ph = V_L = 120 volts

 Phase current = | V_ph | / | Z_ph |

= 120/12 = 10 A

Line current = I_L = √3I_ph

= √ 3× 10 = 17.32 A

Total power = √3 V_L I_L Cos ϕ

= √3 × 120 × 17.32 cos 30°

= 3117.6 watts

Readings of two wattmeters:

W₁ = V_L I_L cos (30 + ϕ )

= 120 × 17.32 cos (30+30) = 1039.2

W₂ = V_L I_L cos (30 -ϕ)

=  120 × 17.32 × cos (30^o – 30^o) ₌ 2078.4

W₁+ W₂ = 1039.2+2078.4

= 3117.6 watts

It is observed that sum of the two wattmeter readings is equal to the power calculated by the formula P =√3 V_L I_L cos ϕ.

15. (a) (i) Derive the relationship between self inductance, mutual inductance and coefficient of coupling.  (8)

Self Inductance

Consider a circuit through which the current changes. So, the flux linking with the circuit also changes. According to Faraday's law of induction an e.m.f. is induced in the circuit. This e.m.f. is equal to rate of change of flux linkage.

i.e., e = N dϕ / dt... (1)

Also e is proportional to time rate of change of current i.e., e ∞ di / dt

 or e = L di / dt..... (2)

From equations (1) and (2), we can write,

L di / dt = N dϕ / dt....(3)

(or) L = N dϕ / di ......(4)

If the permeability is constant then, we can write that,

 L = Nϕ / i .. (5)

L is called self inductance of the circuit.

Definition of L:

The self inductance of a coil is defined as flux linkage in that coil per 1 ampere current in the same coil. It is also defined as the weber turns per ampere current in the coil. L is measured in Henry.

Here, N = No. of turns of the coil

Φ = Magnetic flux in webers

i = current in amperes

 [Note: (i) According to Lenz's law, sign is to be given to the right hand side of the expressions shown in equations (1) & (2).

(ii) The terms N, o and i are confined to only one coil to define 'L']

Mutual Inductance

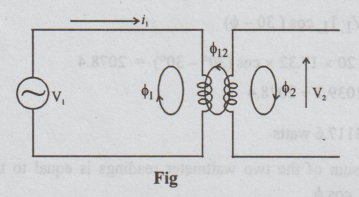
Consider the circuit shown in fig. 8.1, the changing current i₁ produces a variable flux ϕ₁ in the first coil. For the purpose of analysis, ϕ₁ is divided into two components.

ϕ₁ = ϕ₁₁ + ϕ₁₂.............(6)

Here ϕ₁ is the total flux established by i₁, ϕ₁₁ = a part of ϕ₁. It links with coil 1 only but not with coil 2.

ϕ₁₂ =  it is a part of ϕ₁. It links with both coils 2 and 1.

As, the flux linking with coil 2 changes, an e.m.f. is induced in the coil ϕ₂ and is given by

e₂ = N₂ dϕ₁₂ / dt ... (7)

Also, e₂ is proportional to time rate of change of i,. It is because ϕ₁₂ is produced by i1, therefore,

e₂ = M di₁ / dt......(8)

From equations (7) and (8), we can write that,

M = N₂ dϕ₁₂ / di₁...(9)

If the permeability is constant, the above equation becomes

M = N₂ ϕ₁₂ / i₁ ..................(10)

Suppose that the second coil is connected to a voltage source. Let i₂ be the current flow and ϕ₂ be the total flux.

ϕ₂ = ϕ₂₂ +  ϕ₂₁

Here, ϕ₂₁ is a part of ϕ₂ and links with coil 1. Then, the e.m.f. in the coil 1 = e₁.

e₁ = N₁ dϕ₂₁ / dt ... (11)

also e₁ = M di₂ / dt... (12)

Hence M di₂/dt =N₁ dϕ₂₁ / dt

Hence M = N₁ ϕ₂₁ / i₂... (13)

In equations (10 & 13) M is called mutual inductance.

Definition of M

The mutual inductance between 2 coils is defined as the weber turns in one coil per ampere current in other coil. It is measured in henrys.

The mutual inductance is also defined as the ability of one coil to produce e.m.f. in other coil by induction when the current in the first changes.

Coefficient of coupling (K) or coefficient of magnetic coupling (K_M).

Consider the fig. the fraction of the total flux produced by coil 1 linking coil 2 is

It is called ϕ₁₂ / ϕ₁ coefficient of coupling. Thus

K = ϕ₁₂ / ϕ₁ ....(14)

Also K = ϕ₂₁ / ϕ₂... (15)

Multiplying equations (10) & (13), we get

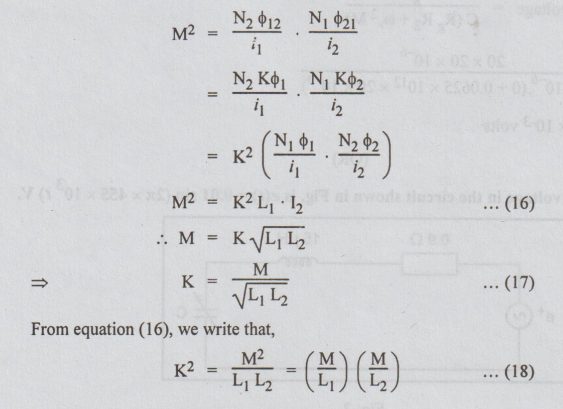
From equation (16), we write that,

K²= M² /L₁L₂ = (M/L₁) (M/L₂)...(18)

From the above expression, we can say that

M/L₁ ,M and M/L₂ are in geometric progression.

Note:

 (i) The values of K depends on spacing, orientation of the coils and on the permeability of the medium.

(ii) It is a non-negative number and is independent of the reference directions of the currents.

(iii) If the coils are at great distance apart, M is very small and hence K.

(iv) For iron-core coupled circuits, K may be as high as 0.99.

(v) For air-core coupled circuits, K varies between 0.4 and 0.8.

(vi) The maximum value of K is 1. Hence Mmax = √L₁ L₂.

 

15. (a) (ii) In the single tuned resonant circuit, the applied voltage in a primary coil E_g = 20 volts (assume R_g=0), R₁=R₂=5Ω L₁=L₂=32µH, M=20 μH

C = (secondary side capacitance) 0.5 μF

Determine the resonant frequency and the output voltage at this frequency.

Solution:

We know ω_r = 1/√L₂ C

 

 (OR)

 

15. (b) (i) The signal voltage in the circuit shown in Fig. is e(t) = 0.01 sin (2π × 455 × 1031) V.

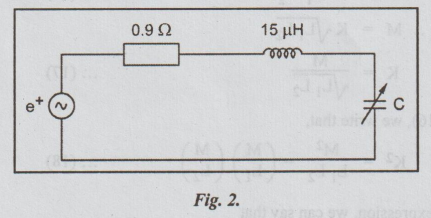
What should be the value of C in order that the circuit would resonate at this signal frequency? At this condition, find the values of I, V_C, Q and bandwidth of the circuit. (10)

Solution:

e  =  0.01 sin (2π × 455 × 10³ t) volts

R = 0.9 Ω

= 15 μH = 15 × 10^-6 H

2π f = 2π × 455 × 10³

f_r = f = 455 × 10³ cps

At resonance:

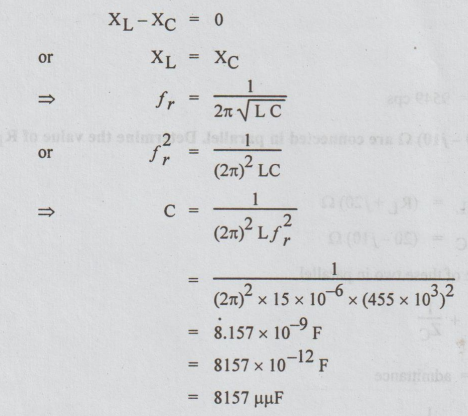
= 8.157 ×10^-9 F

= 8157 × 10^-12 F

= 8157 µµF

At resonance:

I  = I_m = E/R

E =E_m / √2 = 0.01/√2

= 7.07 × 10^-3 volts

I = E / R

= 7.07 × 10^-3 volts

I = E / R

= 7.07 ×10^-3 / 0.9

= 7.86 × 10^-3 A = 7.86 mA

V_C = IX_C

= -7.86 × 10^-3 (1/2πfC)

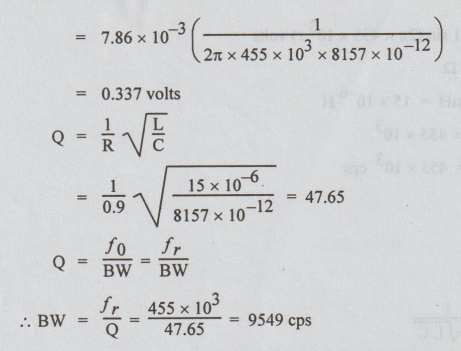
 BW = f_r / Q = 455 × 10³ / 47.65 = 9549 cps

 

15. (b) (ii) (RL+j20) Ω and (20-j10) are connected in parallel. Determine the value of R_L for resonance. (6)

Solution:

Let Z_L = (R_L+ j20)Ω

Z_C = (20 – j10) Ω

Let Z_T be the total impedance of these two in parallel.

Then, 1/Z_T = 1/Z_L = 1/Z_C

1/Z = Y =  admittance

Y_T  = 1/Z_L + 1/Z_C

= 1/R_L + j20 + 1/(20-j10)

After rationalising,

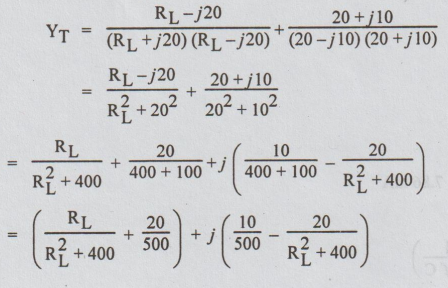
At resonance, the reactive part of Y_T=0

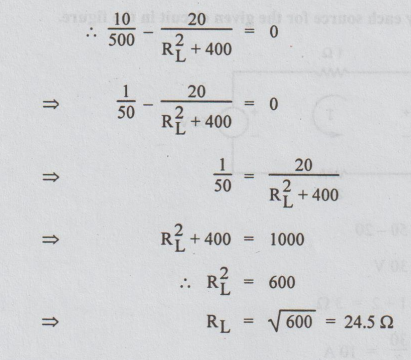
R_L² + 400 = 1000

R_L² = 600

R_L =  √600 = 24.5 Ω