Model Question Paper with Answer - 3 (PART B)

PART-B (5 × 16 = 80 marks)

11. (a) A voltage source of 10Ω with a resistance of 1052, an inductance of 50 mH and a capacitor of 50 μF are connected in series. Calculate the impedance when the frequency is (i) 50 Hz, (ii) 500 Hz, (iii) Power factor at 100 Hz.

Ans:

Z = √ R² + (X_L-X_C)²

X_L =2π fL

X_C = 1 / ωC = 1/ 2π fс

f = 50 Hz

X_L = 2π × 50 × 50 × 10^-3

= 15.7 Ω

 

 (OR)

 

11. (b) Calculate the power delivered by the voltage source of Fig.

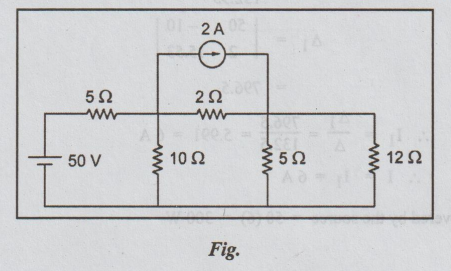
Solution: Let the current from the voltage source be I.

Then power delivered by the source

= V I = 50I

To find I, we shall apply loop current method as done below.

For more simplification, convert the current source into equivalent voltage source and replace the parallel combination of 50 Ω and 12 Ω by a single resistance. Then the circuit becomes as below.

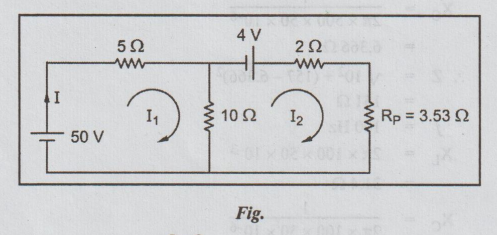
R_P = 5 × 2 / 5 + 12 = 3.53 Ω

Let I₁ and I₂ be the loop currents as shown in the Fig. Error! Reference source not found..

Then by inspection

I₁= Δ₁ / Δ = 796.5 /132.5 == 5.991 = 6 A

I = I₁ = 6 A

Power delivered by the source = 50 (6) = 300 W

 

12. (a) Find the Thevenin's equivalent circuit for the network shown in the figure at the terminals AB.

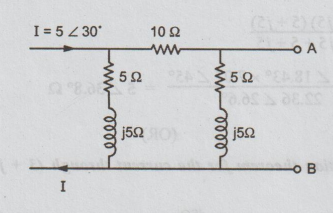
Ans:

Step 1: Thevenin's equivalent between A and B is

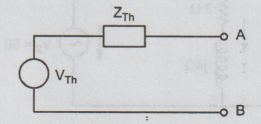
Step 2: To find V_Th or V_oc: Let the current through 10 Ω be I₁.

V_oc = V_AB = V_Th

= I₁ × (5 + j5)

I is divided into 2 parallel paths of impedances ( 5+ j5) and 10 + 5+ j5 = 15 + j5.

Current through 15 + j5 = I₁

By division of current formula,

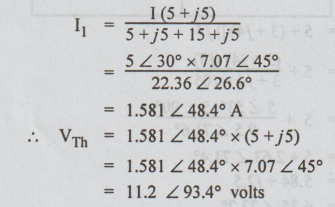
Step 3: To calculate Z_Th:

From the given circuit, kill the current I to obtain the following figure.

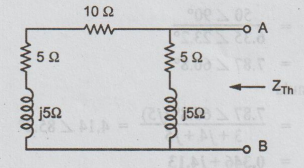
Z_Th =Z_AB = (10 + 5 + j5) || (5 + j5)

 = (15 + j5) (5 + j5) / 15 + j5 + 5 + j5

 = 15.81 ∠ 18.43° × 7.07 ∠ 45° / 22.36 ∠ 26.6° = 5 ∠ 36.8^o Ω

 

 (OR)

 

12. (b) Verify superposition theorem for the current through (3 + j4) branch as shown in the figure.

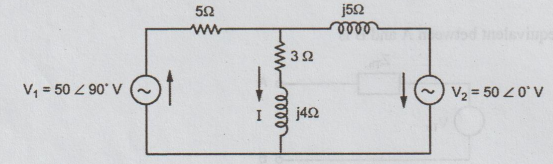
Ans :

Step 1: Let only V1 to act. V₂ is short circuited.

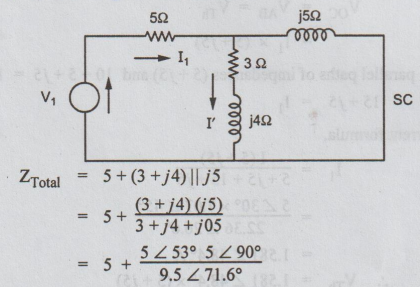
= 5 + 2.63 ∠ 71.4°

= 5.84 + j2.5

= 6.35 ∠ 23.2°

I₁ = V₁ / Z_T

= 50 ∠ 90° / 6.35 ∠ 23.2°

= 7.87 ∠ 66.8°

By current division formula

I' = 7.87 ∠ 66.8° (j5) / 3 + j4 + j5  = 4.14 ∠ 85.2°

= 0.346 + j 4.13

Step 2: Let V₂ source be acting, short circuit V₁.

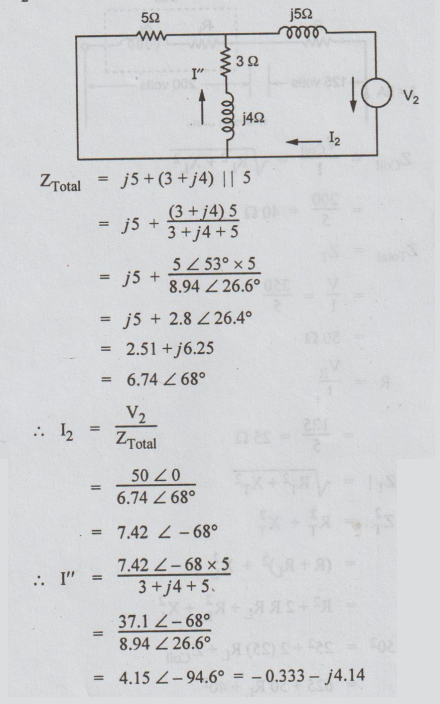
By superposition theorem,

 I = I' - I"

= 0.679 + j8.27

= 8.3 ∠  85° A

 

13. (a) A current of 5 A flows through a non-inductive resistance in series with a coil, when supplied at 250 V, 50 Hz. If the voltage across the resistance is 125 V and that across the coil is 200 V, calculate

(i) Impedance, resistance and reactance of the coil.

(ii) Total power absorbed by the coil.

(iii) Total power. Draw phasor diagram.

Ans :

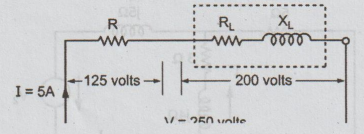
Z_Coil =  V_Coil / I =  √R_L²+X_L²

= 200/5 = 40 Ω

Z_Total = Z_T

= V/I = 250.5

= 50 Ω

R = V_R /I

=125/5 = 25Ω

But,

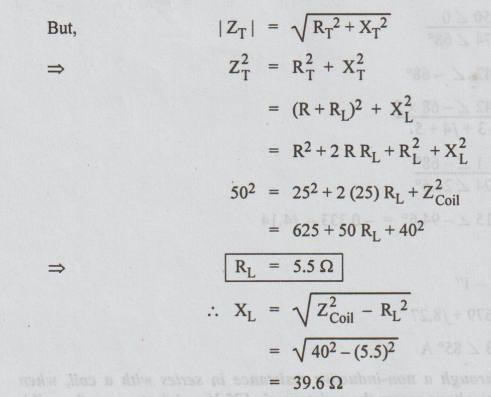
Power absorbed by coil = I²R_L

= (5)² × 5.5

= 138 W

Total p.f. = cos ϕ = R_T/Z_T

= 25 + 5.5 / 50 = 0.61 lag

Total power = VI cos ϕ

= 250 × 5 × 0.61

= 763 W

Phasor diagram

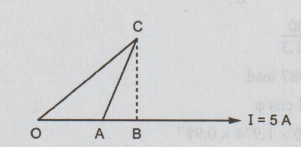
OA = V_R = 125

AB =V_RL

BC = V_XL

AC =V_Coil = 200 V

OC = V = 250 V

 

(ii) A series circuit has R = 100Ω ; L = 50 mH and C = 100 μF and is supplied with 200 V, 50 Hz. Find

1. The impedance

2. The current

3. Power factor

4. The power

5. Voltage drops across each element

Ans: Please refer to Page 3.31 for similar type.

X_L = 2π ƒ L

= 2 × 50 × 50 × 10^-3

= 15.7 Ω

X_L = 1 / 2π ƒ С

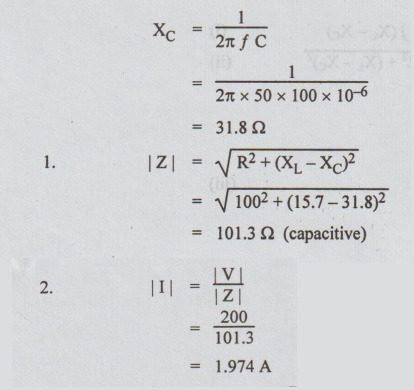
3. Power factor = cos ϕ = R/Z

= 100/101.3

= 0.987 lead

4.Power = VI cos ϕ

= 200 × 1.974 × 0.987

= 390 W

5. V_R= I R

= 1.974 × 100

= 197.4 volts

V_L = I X_L

=1.974 × 15.7

= 31 volts

V_C = I X_C

= 1.974 × 31.8

= 62.8 volts

 

(OR)

 

13. (b) Show that the resonant frequency of a series RLC circuit is f,1/2π √LC

expression for Q factor.

Series Resonance

In a R-L-C series circuit, when the current is in phase with the applied voltage, the circuit is said to be in resonance. Then, phase angle is zero and hence power factor is unity. The circuit acts as purely resistive

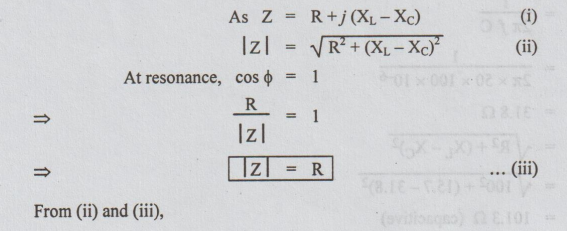
X_L - X_C = 0

X_L = X_C

ω_r L = 1/ ω_rC

ω_r = 1/ √LC

f_r = ω_r / 2π

f_r = 1/ 2π √LC

f_r or f₀ is called resonance frequency. At resonance, in a series circuit the following main effects are to be observed.

 

(b) (ii) A 3 phase delta connected RYB system with an effective voltage of 400 V has a balanced load with impedance (3+j4) Ω Calculate

1.Phase current

2.Line current

3. Power in each phase

Ans: Please refer to Page 6.16 for same type.

Phase voltage = Line voltage = 400 volts

(For delta system)

 

14 (a). Draw the circuit of 3 phase balanced star connected load with wattmeters for power measurement and also prove that two wattmeters are sufficient to measure 3 phase power.

Three Phase Power Measurement Two-Watt Meter Method

This method is applied usually for measuring the electrical power in 3-phase, 3-wire circuit. The load may be balanced or unbalanced. It may be connected either in delta or star.

The current coils of 2 wattmeters are inserted in two of the lines and voltage coil of each wattmeter is connected from its own current coil to the line in which no wattmeter has been connected. The connections of wattmeters in this method are shown in Fig.

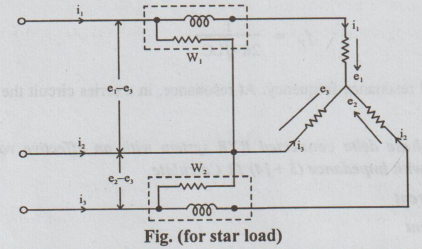
Let e₁, e₂ and e₃ be the voltages of the three loads at particular instant and i₁, i₂ and i₃ be the currents of the three loads i.e., these voltages and currents are called instantaneous values. Hence, the power at the instant under consideration is equal to the sum of their products, regardless of power factor

i.e., Instantaneous power = P= e₁i₁ + e₂i₂ + e₃i₃ ... (1)

Case (1) Load - Star connected

Since all the three-phases meet at a star point, application of KCL yields

i₁+i₂+ i₃ = 0

or i₃ =  - (i₁+i₂)

Substituting i₃ = - (i₁ + i₂) in expression (1) we get

p = e₁i₁ + e₂i₂ - e₃(i₁ +i₂)

= i₁ (e₁ - e₃) + i₂ (e₂ - e₃)

Here i₁ = the instantaneous current flowing through the current coil of wattmeter. (e₁-e₃)= the instantaneous potential difference across voltage coil of wattmeter 1.

Therefore i₁ (e₁ - e₃)= w₁. w₁ is the instantaneous power measured by wattmeter 1.

i₂ = The instantaneous currents flowing through the current coil of wattmeter 2. (e₂ - e₃) = instantaneous potential difference across the voltage coil of wattmeter 2.

i₂ (e₂ - e₃) = w₂. w₂ is the instantaneous power measured by watt meter 2.

Hence p = w₁ + w₂ or total average power = P = W₁ +  W₂.

Hence, the algebraic sum of readings of the two wattmeters gives the total power in the 3-phase, 3- wire star connected load. It is valid for both balanced and unbalanced loads.

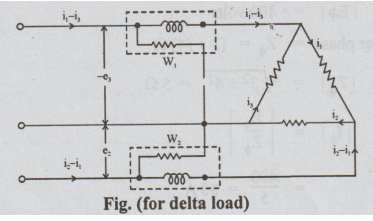
Case (2) Load - delta connected

In delta connected system, the 3-phases form a close loop. According to KVL,

e₁+e₂+ e₃ = 0

Or e₁ = - (e₂+ e₃)

From equation (1), p = e_ii₁ + e₂i₂ + e₃i₃

= - (e₂+ е₃) i₁ + е₂i₂ + e₃i₃

= -e₃ (i₁ - i₃) + e₂ (i₂ - i₁)

- e₃ is the instantaneous p.d. across the voltage coil of wattmeter 1.

(i₁ - i₃) the current flowing through wattmeter 1. So, first wattmeter reads - e₃ (i₁- i₃). Similarly, the second wattmeter reads e₂ (i₂ - i₁).

Hence, the total instantaneous power = p = w₁ + w₂ and the total average power = P = W₁ + W₂.

Thus, the algebraic sum of the readings of the two wattmeters gives the total power of the circuit. It is true for both balanced and unbalanced loads and for star as well as delta connected systems.

 

(OR)

 

14. (b) Derive the formula for total power consumed in unbalanced Y connected load.

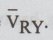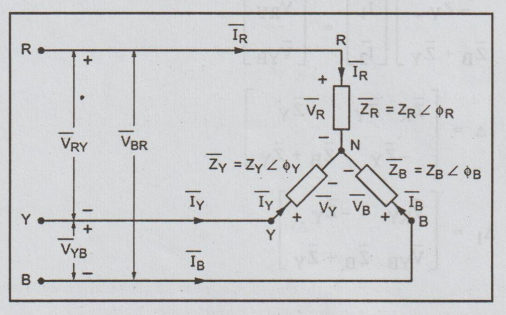
Let us assume a phase sequence of RYB. Let the reference phases be . The three wire three phase star connected unbalanced load with conventional polarity of voltages and direction of currents is shown in Fig.

The line voltages of the supply source for RYB sequence are,

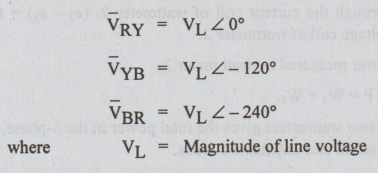
In unbalanced star connected load, it will be easier to solve, the line currents by assuming two sources, across the lines whose values are equal to corresponding line voltages. Consider the circuit in Fig. in which a voltage source of value  is connected across lines R and Y and a voltage source of value  is connected across Y and B.

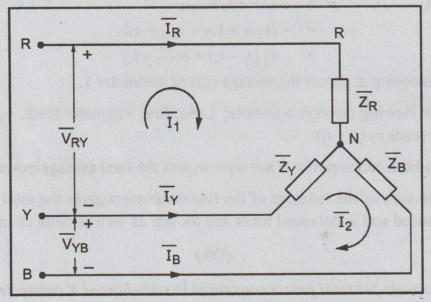
The circuit of Fig. has two meshes, hence we can assume two mesh currents 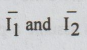as shown in the Fig. The mesh basis matrix equation is

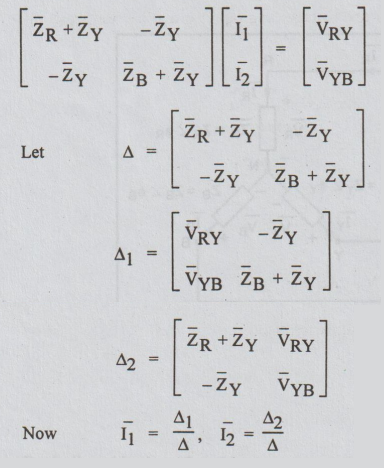
From the mesh currents the line currents can be obtained

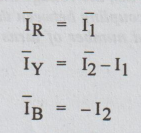
In star connected load the phase currents are same as that of the line currents. Therefore the phase and line currents in the polar form can be written as

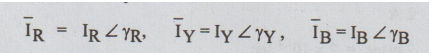
where 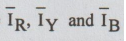 are the magnitude of line and phase currents and ɤ_R, ɤ_Y, and ɤ_B are phase angle of line and phase currents with respect to reference phasor.

Now the phase voltages are given by the product of phase current and phase impedance. Therefore the phase voltages are,

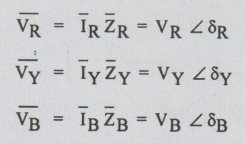
where V_R, V_Y and V_B are magnitude of phase voltages and δ_R, δ_Y and δ_B are phase angle of phase voltages with respect to reference phasor.

Power consumed by three phase load, P

 

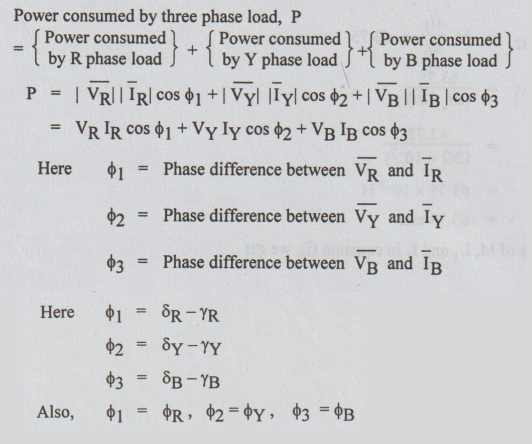
15. (a) The number of turns in a coil is 250. When a current of 2 A flows in this coil, the flux in the coil is 0.3 mwb. When this current is reduced to zero in 2 ms, the voltage induced in a coil lying in the vicinity of coil is 63.75 volts. If the coefficient of coupling between the coils is 0.75, find self-inductance of the two coils, mutual inductance and number of turns in the second coil.

Ans: Data:

N₁ = 250

I₁ = 2 A

ϕ_{1 =} 0.3 mwb = 0.3 × 10^-3 wb

di₁= 2 A

dt = 2 msec = 2 × 10^-3 sec

e_M2 = 63.75 volts

K = 0.75

Required: (a) L₁ (b)L₂ (c) M, (d) N2.

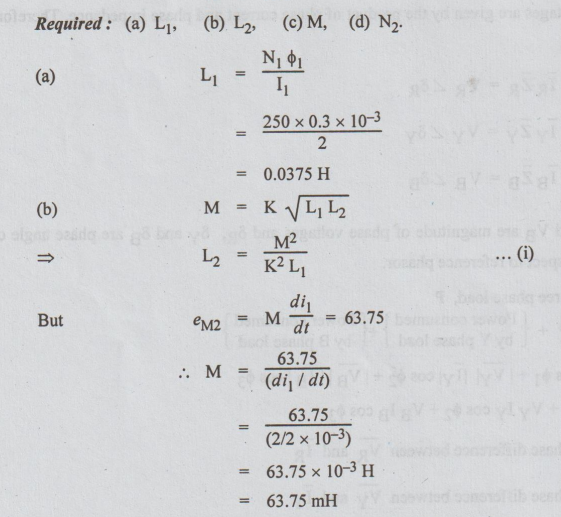
Substituting these values of M, L1 and K in equation (i), we get

 

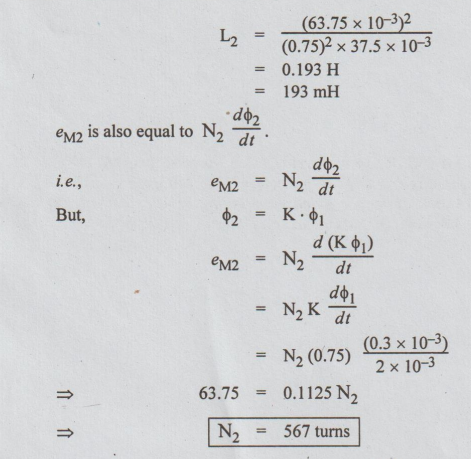
 (OR)

 

15. (b) Two identical coupled coils in series has an equivalent inductance values of 0.084 H and 0.0354 H. Find the values of L₁, L₂, M and K.

Ans: As the coils are identical,

L₁ = L₂ = L (say)

L₁ +  L₂ + 2 M = 0.084

L₁ + L₂ - 2 M = 0.0354

Adding, 2 (L₁+ L₂ ) = 0.1194

2 (L + L) = 0.1194

 L = 0.02985 H

.L₁ =L₂ = L = 0.02985 H

= 29.85 mH