Digital Logic Circuits: Unit II: Combinational Circuits
Multiplexers
Block and Logic diagram, Logic symbol, Function table, Equivalent circuit, Working
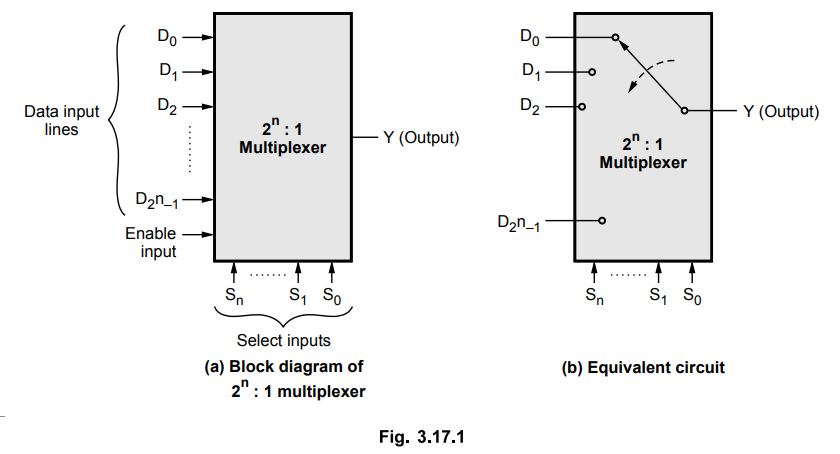
• In digital systems, many times it is necessary to select single data line from several data-input lines, and the data from the selected data line should be available on the output. The digital circuit which does this task is a multiplexer.
Multiplexers
AU
: Dec.06, 11, 12, 15, May-07, 11, 12, 16, 17
•
In digital systems, many times it is necessary to select single data line from
several data-input lines, and the data from the selected data line should be
available on the output. The digital circuit which does this task is a
multiplexer.
•
It is a digital switch. It allows digital information from several sources to
be routed onto a single output line, as shown in the Fig. 3.17.1. The basic
multiplexer has several data-input lines and a single output line. The
selection of a particular input line is controlled by a set of selection lines.
Since multiplexer selects one of the input and routes it to output, it is also
known as data selector. Normally, there are 2n input lines and n selection
lines whose bit combinations determine which input is selected. Therefore,
multiplexer is 'many into one' and it provides the digital equivalent of an
analog selector switch.
1. 2 : 1 Multiplexer
•
Fig. 3.17.2 (a) shows 2 : 1 multiplexer. DQ is applied as an input to one AND
gate and Dj is applied as an input to another AND gate. Enable input is applied
to both gates as one input. Selection line S is connected as second input to
second AND gate. An inverted S is applied as second input to first AND gate.
Outputs of both AND gates are applied as inputs to OR gate.

Working
•
When E = 0, output is 0, i.e. Y = 0 irrespective of any input condition. When E
= 1 the circuit works as follows :
•
When S = 0, the inverted S, that is 1 gets applied as second input to first AND
gate. Since S is applied directly as input to second AND gate; its output goes
zero irrespective of first input. Since the second input of first AND gate is
1, its output is equal to its first input, that is DQ. Hence Y = DQ.
•
Exactly opposite is the case when S = 1. In this case, second AND gate output
is equal to its first input D1 and first AND gate output is 0. Hence Y = Dp
Both these cases are summarized in truth table shown in Fig. 3.17.2 (b).
Deriving
realization expression
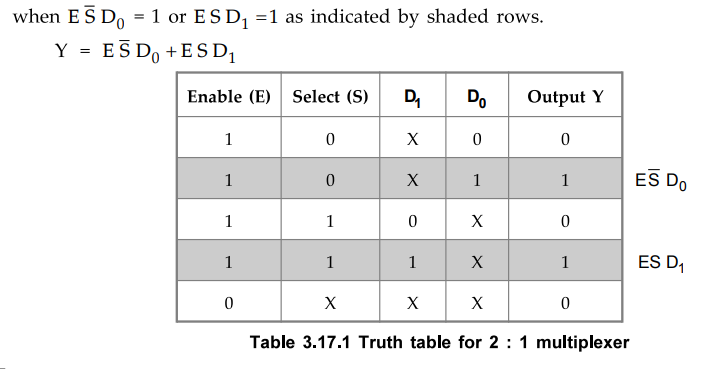
• The Table 3.17.1 shows the truth table for 2 : 1 multiplexer. From the truth table it is clear that Y = 1
2. 4 : 1 Multiplexer
•
Fig. 3.17.3 (a) shows 4-to-l line multiplexer. Each of the four lines, DQ to
D3, is applied to one input of an AND gate. Selection lines are decoded to
select a particular AND gate.

•
For example, when S1S0 = 0 1, the AND gate associated
with data input D1 has two of its inputs equal to 1 and the third
input connected to Dr The other three AND gates have at least one input equal
to 0, which makes their outputs equal to 0. The OR gate output is now equal to
the value of D1, thus we can say data bit D1 is routed to
the output when S1 S0 = 0 1.
3. 8 : 1 Multiplexer
• Fig. 3.17.4 shows 8 : 1 multiplexer.
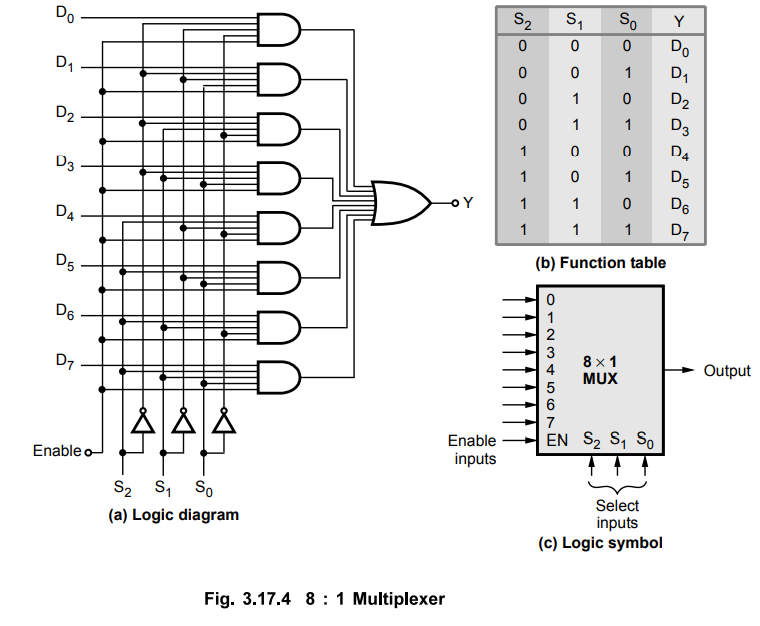
•
There are eight input lines one output line and three select lines. As shown in
the function table, the selection of a particular input line is controlled by
three selection lines.
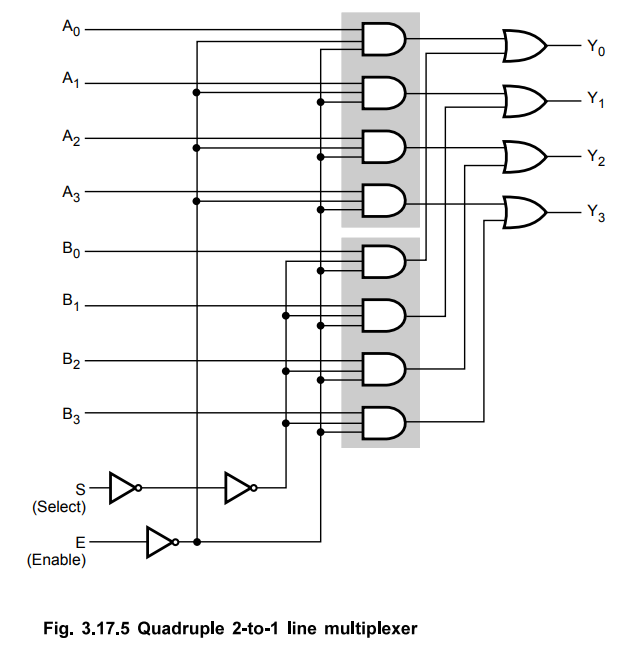
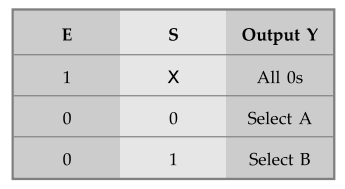
4. Quadruple 2 to 1 Multiplexer
•
In some cases, two or more multiplexers are enclosed within one IC package, as
shown in the Fig. 3.17.5. The Fig. 3.17.5 shows quadruple 2-to-l line
multiplexer, i.e. four multiplexers, each capable of selecting one of two input
lines. Output Y1 can be selected to be equal to either Ax or Br
Similarly output Y2 may have the value of A2 or B2,
and so on. The selection line S selects one of two lines in all four
multiplexers. The control input E enables the multiplexers in the 0 state and
disables them in the 1 state. When E = 1, outputs have all 0's, regardless of
the value of S.
Function
Table :
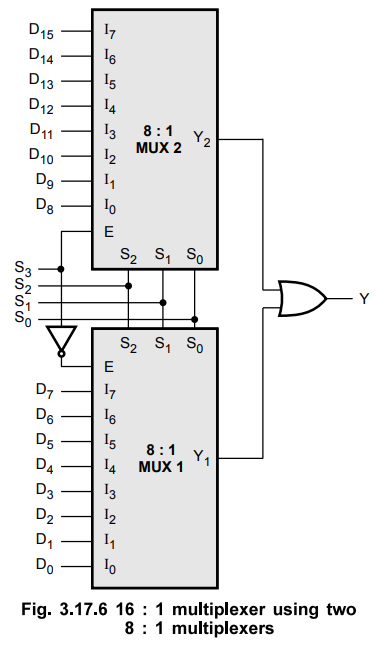
5. Expanding Multiplexers
•
It is possible to expand range of inputs for multiplexer beyond the available
range by interconnecting several multiplexers in cascade. The circuit with two
or more multiplexers connected to obtain the multiplexer with more number of
inputs is known as multiplexer tree.
Examples
for Understanding
Step
1 :
Connect the select lines (S2, S1 and S0) of
two multiplexers in parallel.
Step
2 :
Connect most significant select line (S3) such that when S3 =
0 MUX1 is enabled and when S3 = 1, MUX2 is enabled.
Step
3 :
Logically OR the outputs of two multiplexers to obtain the final output Y.
Ex.
3.17.2 Design 16 : 1 multiplexer using 4 : 1 multiplexers.
Sol.
:
Since there are 16-inputs for the multiplexers we require four 4:1 multiplexers
to satisfy input needs. The four outputs of 4 : 1 multiplexers are again
multiplexed by 4 : 1 multiplexer to generate final output.
Step
1 :
Connect the select lines (S1 and S0) of four multiplexers
in parallel.
Step
2 :
Connect the most significant select lines (S3 and S2) to the MUX5.
Step
3 :
Connect the outputs Y0, Y1
, Y2 and Y4 of four multiplexers as data inputs for
the MUX 5, as shown in the Fig. 3.17.7.

Examples
with Solutions
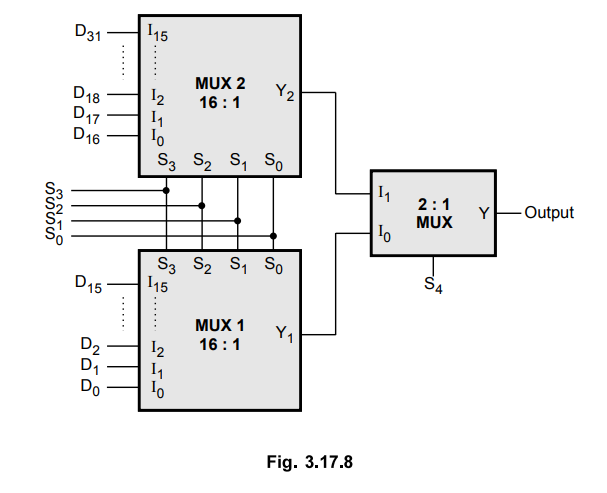
Ex.
3.17.3 Draw 32 : 1 multiplexer using two 16:1 multiplexers and one 2 : 1
multiplexer.
Solution
:
The Fig. 3.17.8 shows the connection diagram for 32 : 1 multiplexer using two
16 : 1 multiplexer and one 2 : 1 multiplexer. Here, select lines S0,
S1, S2 and S3 are connected in parallel to 16
: 1 multiplexers and select line S4 is used to select either Y1 or Y2
using 2 : 1 multiplexer.
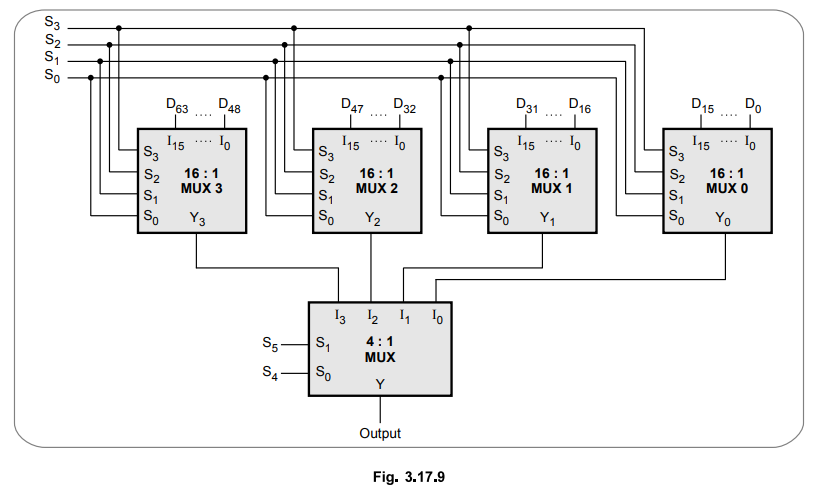
Ex.
3.17.4 Draw 64 : 1 multiplexer tree using 16 : 1 multiplexer.
Sol.
:
The Fig. 3.17.9 shows 64 : 1 multiplexer using four 16 : 1 multiplexers and one
4 : 1 multiplexer.
Examples
for Practice
Ex.
3.17.5 Draw the block diagram of a 4 : 1 multiplexer using 2 : 1 MUX.
Ex.
3.17.6 Design 32 : 1 MUX using 8 : 1 MUX.
6. Implementation of Combinational Logic using MUX
•
A multiplexer consists of a set of AND gates whose outputs are connected to
single OR gate. Because of this construction any Boolean function in a SOP form
can be easily realized using multiplexer. Each AND gate in the multiplexer
represents a minterm. In 8 to 1 multiplexer, there are 3 select inputs and 23
minterms. By connecting the function variables directly to the select inputs, a
multiplexer can be made to select the AND gate that corresponds to the minterm
in the function. If a minterm exists in a function, we have to connect the AND
gate data input to logic 1; otherwise we have to connect it to logic 0. This is
illustrated in the following example.
Examples
for Understanding
Ex.
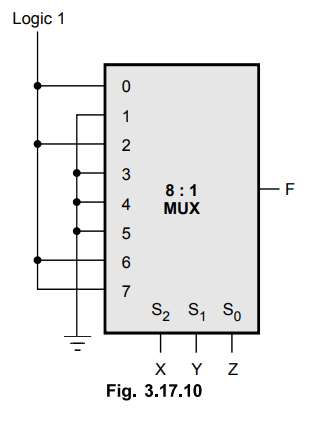
3.17.7 Implement the given function using multiplexer.
F(x,y,z)
= ∑ (0,2, 6, 7).
Sol.
:
Step
1 :
Select the multiplexer. Here, Boolean expression has 3 variables, thus we
require 23 = 8:1 multiplexer.
Step
2 :
Connect inputs corresponds to the present minterms to logic 1.
Step
3 :
Connect remaining inputs to logic 0.
Step
4 :
Connect input variables to select lines of MUX.
Ex.
3.17.8 Implement the Boolean function represented by the given truth table
using multiplexer.

Sol.
:
Step
1 :
Select the multiplexer. Here, there are three input variables, thus we require
23 = 8 : 1 multiplexer.
Step
2 :
Find the minterm expression.
Minterm
expression for given truth table is∑ m (1, 2, 5, 7).
Step
3 :
Connect inputs corresponds to the present minterms to logic 1.
Step
4 :
Connect remaining inputs to logic 0.
Step
5 :
Connect input variables to select lines of MUX.
In
the above example, we have seen the method for implementing Boolean function of
3 variables with 2 (8) - to -1 multiplexer. Similarly, we can implement any
Boolean function of n variables with 2n-to-l multiplexer. However,
it is possible to do better than this. If we have Boolean function of n + 1
variables, we take n of these variables and connect them to the selection lines
of a multiplexer.
The
remaining single variable of the function is used for the inputs of the
multiplexer. In this way we can implement any Boolean function of n variables
with 2 n-1 to-1 multiplexer.
Let us see some example.
Examples
for Understanding
Ex.
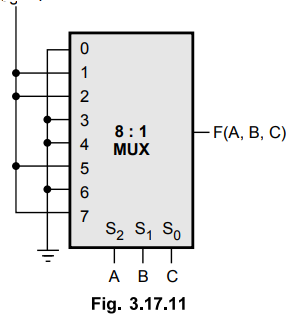
3.17.9 Implement the following Boolean function using 4 : 1 multiplexer.
F(A,
B, C) = ∑m(1, 3, 5, 6)
Sol.
:
Step
1 :
Connect least significant variables as a select inputs of multiplexer. Here,
connect C to S0 and B to S1.
Step
2 :
Derive inputs for multiplexer using implementation table.

As
shown in the Fig. 3.17.12 (a) the implementation table is nothing but the list
of the inputs of the multiplexer and under them list of all the minterms in two
rows. The first row lists all those minterms where A is complemented and the
second row lists all the minterms with A uncomplemented. The minterms given in
the function are circled and then each column is inspected separately as follows
:
•
If the two minterms in a column are not circled, 0 is applied to the
corresponding multiplexer input (see column 0).
•
If the two minterms in a column are circled, 1 is applied to the corresponding
multiplexer input (see column 1).
•
If the minterm in the second row is circled and minterm in the first row is not
circled, A is applied to the corresponding multiplexer input (see column 2).
•
If the minterm in the first row is circled and minterm in the second row is not
circled, A is applied to the corresponding multiplexer input (see column 3).
Ex.
3.17.10 Implement the following Boolean function using 8 :1 multiplexer
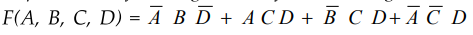
Sol. : Step 1 : Express Boolean function in the minterm form.
The
given Boolean expression is not in standard SOP form. Let us first convert this
in standard SOP form
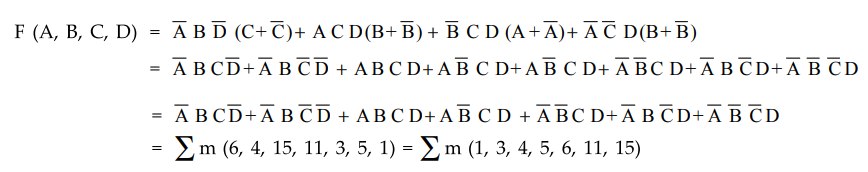
Step
2 :
Implement it using implementation table.
From
the Boolean function in the minterm form can be implemented using 8 : 1
multiplexer as follows :

Ex.
3.17.11 Implement the following Boolean function with 8 : 1 multiplexer
F(A,
B,C,D) = πM (0, 3, 5, 8, 9, 10, 12, 14)
Sol.
:
Here, instead of minterms, maxterms are specified. Thus, we have to circle
maxterms which are not included in the Boolean function. Fig. 3.17.14 shows the
implementation of Boolean function with 8 :1 multiplexer.

Ex.
3.17.12 Implement the following Boolean function with 8 : 1 multiplexer.
F(A,
B, C,D) = ∑ m(0, 2, 6, 10, 11, 12, 13) + d (3, 8, 14)
Sol.
:
In the given Boolean function three don't care conditions are also specified.
We know that don't care conditions can be treated as either Os or Is. Fig.
3.17.15 shows the implementation of given Boolean function using 8 : 1
multiplexer.
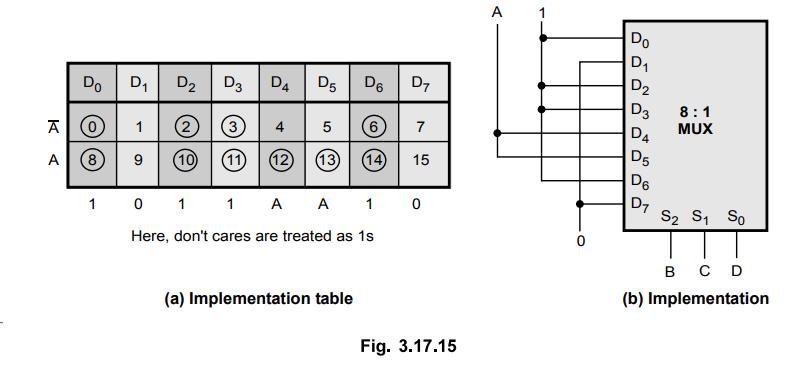
In
this example, by taking don't care conditions 8 and 14 as Is we have eliminated
A term and hence the inverter.
Examples
with Solutions
Ex.
3.17.13 Implement full adder circuit using 8 : 1 multiplexer.
Sol
.:

Ex.
3.17.14 Implement full adder circuit using quadruple 2 to 1 multiplexer.
Sol.
: Implementation tables :

Examples
for Practice
Ex.
3.17.15 Implement the following function using 8 :1 multiplexer.
f(a,
b, c, d) = ∑m (0, 1, 5, 6, 8, 10, 12, 15)
Ex.
3.17.16 Implement Boolean function 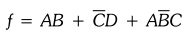 using
8 : 1 multiplexer.
using
8 : 1 multiplexer.
Ex.
3.17.17 Implement the following function f (A, B, C) = ∑m(0, 3, 5) using 8:1
multiplexer.
7. Applications of Multiplexer
1.
They are used as a data selector to
select one out of many data inputs.
2.
They can be used to implement combinational logic circuit.
3.
They are used in time multiplexing systems.
4.
They are used in frequency multiplexing systems.
5.
They are used in A/D and D/A converter.
6.
They are used in data acquisition systems.
8. Multiplexer ICs

Review Questions
1. Define multiplexer.
2. What is data selector ?
3. Draw and explain the working of2:l multiplexer and realize it
using basic gates.
4. Explain 4 : 1 multiplexer with the help of logic circuit and
truth table.
5. Explain 8 : 1 multiplexer with the help of logic circuit and
truth table.
6. Explain the concept and working of quadruple 2 to 1 line
multiplexer.
7. State the applications of multiplexers.
8. Write brief note on multiplexer.
Digital Logic Circuits: Unit II: Combinational Circuits : Tag: : Block and Logic diagram, Logic symbol, Function table, Equivalent circuit, Working - Multiplexers
Related Topics
Related Subjects
Digital Logic Circuits
EE3302 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
