Parallel Adder

Parallel Adder

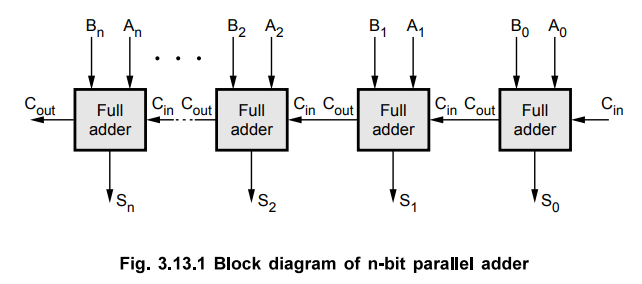
• We have seen, a single full-adder is capable of adding two one-bit numbers and an input carry. In order to add binary numbers with more than one bit, additional full-adders must be employed. A n-bit, parallel adder can be constructed using number of full adder circuits connected in parallel. Fig. 3.13.1 shows the block diagram of n-bit parallel adder using number of full-adder circuits connected in cascade, i.e. the carry output of each adder is connected to the carry input of the next higher-order adder.

• It should be noted that either a half-adder can be used for the least significant position or the carry input of a full-adder is made 0 because there is no carry into the least significant bit position. 

Ex. 3.13.1 Design a 4-bit parallel adder using full-adders.

Sol. : Fig. 3.13.2 shows the block diagram for 4-bit adder. Here, for least significant position, carry input of full-adder is made 0.

Review Questions

1. What is parallel adder ?

2. Draw and explain the working of 4-bit parallel adder.

3. Design a 4-bit binary ripple carry adder with full adders and discuss its operation.