Parameters Related to Corona

Parameters Related to Corona

AU : May-06, 07, 13, 14, 15, Dcc.-03, 05, 12, 16

The various parameters related to corona effect are, i) Critical disruptive voltage, ii) Critical visual disruptive voltage and iii) Corona power loss

 

1. Critical Disruptive Voltage

The critical disruptive voltage is defined as the minimum phase to neutral voltage at which corona occurs. It is denoted as V_d.

For a given transmission conductor, the gradient is maximum at the surface i.e. at a distance of radius r from the centre. So if there are two conductors each of radius r and distance between them is d then the potential gradient at the surface of the conductor is given by,

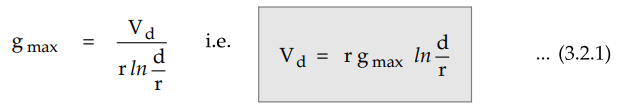
At the critical disruptive voltage, the complete disruption of dielectric occurs. At this voltage, the potential gradient developed is equal to breakdown strength of the air which is denoted as go. At a normal temperature of 251 and pressure of 76 cm of Hg the value of go is 30 kV/cm.

Hence V_d can be expressed as,

V_d = rgo ln d / r ... (3.2.2)

But for any other temperature and pressure the value of go is different. It is given by,

g'o = δ go where δ = Air density correction factor         ... (3.2.3)

The air density correction factor which depends on the pressure and temperature is given by,

δ = 3.92 b / 273 + t  ... (3.2.4)

where

b = Barometric pressure in cm of Hg and t = Temperature in ° C

Hence V_d can be further expressed as,

Vd = rδgo ln = d / r ... (3.2.5)

The equation (3.2.5) is valid if the conductors are solid and having uniform smooth surface. But the surface conditions are different for large cables and stranded conductors. Hence another correction factor must be introduced in Vd. Such a factor is called irregularity factor denoted as mo. This factor is the average value of the ratio of breakdown voltage for irregular conductor to the smooth conductor.

The table gives the values of m_o for various cases.

Hence the final expression for the critical disruptive voltage becomes,

 

2. Critical Visual Disruptive Voltage

When the voltage applied is equal to critical disruptive voltage, the corona starts but it cannot be visible. To have it visible, the charged ions in air require further ionization and hence surface gradient must increase and reach a value g_v. The voltage required to cause a gradient of g_v at the surface is called critical visual disruptive voltage denoted as V_v.

The critical visual disruptive voltage is the minimum phase to neutral voltage at which corona glow appears and visible all along the conductors.

The distance between gv and go is called the energy distance which is equal to (r + 0.301 √r) for two parallel conductors and (r + 0.308 √r) for co-axial conductors. Thus g T is not constant and depends on the size of the conductors. It is given by,

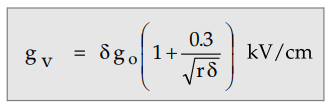 ... (3.2.7)

This is for parallel conductors. 

The irregularity factor is slightly different denoted as mv. Its value is 1.0 for polished conductors, 0.98 to 0.93 for rough conductors and 0.72 for the local corona on stranded conductors. For the general corona its value is 0.82. The conductor surface is not regular and hence corona does not start simultaneously all along the surface. It starts at the portions which are pointed. This is called local corona.

Considering all these factors the critical visual disruptive voltage can be expressed as,

If V_d and V_v r.m.s. values are to be calculated then r.m.s. value of g_o must be used.

 

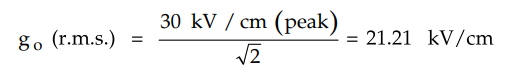
3. Corona Power Loss

The ions produced in the air due to corona are moving. The energy required to keep them moving is derived from the supply system. This additional power required which is dissipated in the form of heat, sound and light in case of corona, is called corona loss.

The expression for the corona loss is given by Peek as,

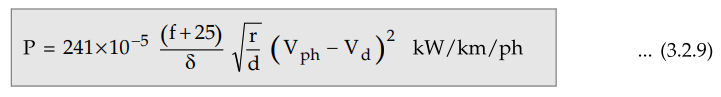
where  f = Supply frequency in Hz

V_ph = Phase to neutral r.m.s. voltage in kV

V_d = Critical disruptive voltage (r.m.s.) per phase

The above formula is called Peek's formula and applicable for fair conditions.

Key Point If the weather is rainy and stormy then critical disruptive voltage Vd gets reduced by the factor 0.8.

Hence corona power loss in rainy conditions is given by,

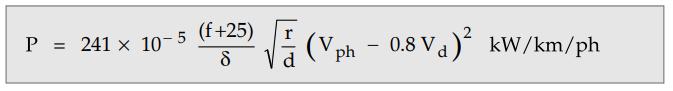
The formula is useful when corona losses are predominant and the ratio of (V_ph/V_d) is above 1.8. 

If the ratio of (V_ph/V_d) is less than 1.8, Peterson's formula must be used, which is given by,

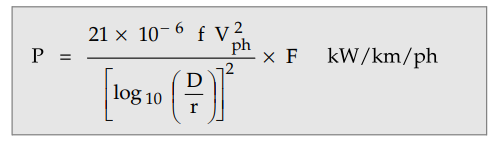
where F is the factor which varies as the ratio V_ph/V_d given by,

The corona loss in 3 phase extra high voltage lines, having voltage level more than 400 kV, in rainy condition is given by,

where          P_3ϕ - Total three phase loss in rainy condition for EHV line

P_3ϕ - Total three phase loss in fair condition for EHV line

J - Constant = 4.37 × 10^-10 at 400 kV

K - Wetting coefficient = 10

i - Subconductor

m - Total number of subconductors

V_i - Voltage gradient on outer conductor in kV/cm

p - An exponential index generally 5

 

Example 3.2.1 Determine the critical disruptive voltage and the critical visual disruptive voltage for a 3 phase, 50 Hz, 132 kV line situated in a temperature of 30°C and at a barometric pressure of 74 cm. The conductor diameter is 1.5 cm while the equilateral spacing between the conductors is 2.75 m. The surface irregularity factor is 0.9 while mv = 0.75.

Solution : Given b = 74 cm and t = 30 ° C

 

Example 3.2.2 A particular 3 phase transmission line has total corona loss of 57 kW at 110 kV and corona loss of 99 kW at 114.8 kV. Calculate the critical disruptive voltage per phase and corona loss at 120 kV.

Solution : The total corona loss is given by,

P = 3 × Corona loss per phase

This is the total corona loss at 120 kV of system line voltage.

 

Example 3.2.3 A 3 phase overhead line operates at 132 kV, 50 Hz. The conductors are spaced at the corners of an equilateral triangle with a spacing of 3 m between centres. Determine the conductor diameter required to prevent corona under fair weather conditions. The air temperature is 22°C and barometer pressure is 72.5 cm, V_d = 150 kV.

Solution: b = 72.5 cm, t = 22°C, d = 3 m = 300 cm

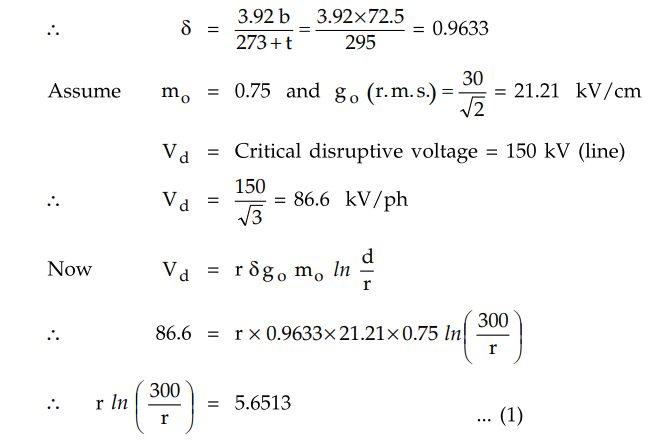
The equation cannot be solved mathematically. Use trial and error method.

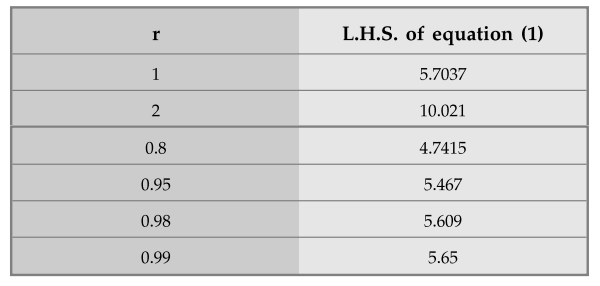
Hence the radius of the conductor is 0.99 cm.

So conductor diameter to prevent corona must be 1.98 cm, under fair weather conditions.

 

Example 3.2.4 A 132 kV, 3 phase line with 1.956 cm diameter conductors in built so that corona takes place, if the line voltage exceeds 210 kV (r.m.s.). If the value of potential gradient at which ionization occurs can be taken as 30 kV per cm, find the spacing between the conductors.

Solution :

 

Example 3.2.5 A conductor with 2.5 cm dia is passed centrally through a porcelain bushing having er = 4 and internal and external diameters of 3 cm and 9 cm, respectively. The voltage between the conductor and an earthed clamp surrounding the porcelain is 20 kV r.m.s. Determine whether corona will be present in the air-space round the conductor. Solution : Let g 1max = Maximum gradient on the surface of conductor.

Solution :

This exceeds the gradient of air 21.1 kV/cm hence corona will be present in the air space round the conductor.

 

Example 3.2.6 A three phase, 50 Hz, 220 kV transmission line consists of conductor of 2.0 cm diameter and spaced equilaterally at a distance of 4 m. The line conductors have smooth surface with value of surface irregularity factor 0.96. The barometric pressure is 73 cm of Hg and temperature of 20 °C. Determine the fair and stormy weather corona loss per km per phase.

Solution : b = 73 cm, t = 20 °C, d = 4 m = 400 cm, mo = 0.96, f = 50 Hz

 

Example 3.2.7 A 3-phase transmission line is having three conductors equilaterally spaced 6 m apart. The diameter of each conductor is 2 cm. The air temperature is 27 °C and pressure is 72 cm of Hg. If the surface factor is 0.82 and irregularity factor is 0.9, find the critical disruptive and visual disruptive voltages.

AU: May-07, Marks 8

Solution: Given: b = 72 cm, t = 27 °C, m = 0.9 m m_v = 0.82

 

Example 3.2.8 Estimate the corona loss for a three-phase, 110 kV, 50 Hz, 150 km long transmission line consisting of three conductors each of 10 mm diameter and spaced 2.5 m apart in a equilateral triangle formation. The temperature of air is 30° C and the atmospheric pressure is 750 mm of mercury. Assume the irregularity factor as 0.85. Ionization of air may be assumed to take place at a maximum voltage gradient of 30 kV/cm.

Solution : b = 750 mm = 75 cm, t = 30° C, d = 2.5 m = 250 cm, 

Review Questions

1. Explain disruptive critical voltage.

2. Explain visual critical voltage.

3. Write a short note on corona power loss.

4. Write a Peek’s formula used for calculating corona loss under fair weather conditions and under storm conditions.

5. A 3-phase transmission line is having three conductors equilaterally spaced 6 m apart. The diameter of each conductor is 2 cm. The air temperature is 27 °C and pressure is 72 cm of Hg. If the surface factor is 0.82 and irregularity factor is 0.9, find the critical disruptive and visual disruptive voltages.        

[Ans.: 198.981 kV (line), 237.367 kV (line)]

6. A three phase equilaterally spaced transmission line has a total corona loss of 53 kW at 106 kV and a loss of 98 kW at 110.9 kV. What is the disruptive critical voltage between lines ? What is corona loss at 113 kV ?

[Ans.: 92.3815 kV, 120.906 kW]

7. A3 phase line has conductors of 2 cm in diameter, spaced equilaterally, 1 m apart. If the dielectric strength of air is 30 kV/cm (max), find the critical disruptive voltage for the line. Air density factor 8 = 0.952 and irregularity factor mo = 0.9.      

[Ans.: 144.95 kV (r.m.s.)]

8. A 3 phase, 50 Hz, 132 kV transmission line consists of conductors of 1.17 cm diameter and spaced equilaterally at a distance of 3 m. The conductors have smooth surface with mo = 0.96. The barometric pressure is 72 cm ofHg and the temperature is 20°C. Determine corona loss per km per phase under fair and foul weather conditions.

[Ans.: 0.1767 kW/km/phase, 2.9716 kW/km/phase]

9. Find the corona characteristics of a 110 kV, 50 Hz, 3 phase transmission line 175 km long consisting of three 1 cm diameter stranded conductors arranged in the form of a delta with a spacing of 3 m. The barometric pressure is 74 cm of mercury and temperature 26 ° C, surface factor is 0.85. For local corona, surface factor is 0.72 and it is 0.82 for general corona.

[Ans.: 55.64 kV(r.m.s.) per phase, 67.442 kV/ph (r.m.s.), 76.809 kV/ph (r.m.s.), 247.246 kW, 1441.095 kW, 20.16 kW]