Potential at a Conductor in a Group of Charged Conductors

Potential at a Conductor in a Group of Charged Conductors

The potential difference between any two points is nothing but the work done in joules per coulomb required to move a coulomb of charge between the two points. The force on a charge in the field is measured by electric field intensity which is equal to the force in newtons per coulomb on a coulomb of charge at the point considered and is measured in volts per metre.

Consider a long straight wire carrying positive charge of q c/m as shown in the Fig. 1.26.1.

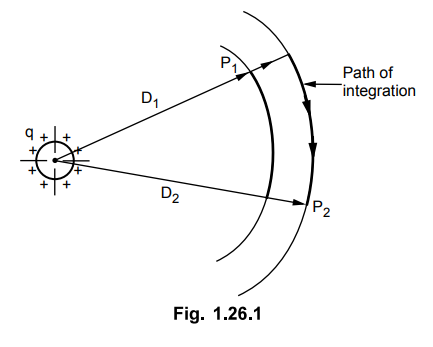
Consider two points P₁ and P₂ located at a distances of D₁ and D₂ from centre of wire. There is positive charge on wire which will repel when a positive charge is placed in the field. If we want to move charge from point P₂ to P₁ then work must be done on positive charge. Here Pi is at higher potential than P2. If the charge moves from P₁ to P₂, it expends energy which is nothing but voltage drop from P₁ to P₂. The path followed does not affect the potential difference.

In order to find the voltage drop from Px to P2 is to obtain the voltage between equipotential surfaces passing through P₁ and P₂.

The voltage drop between P₁ and P₂ is,

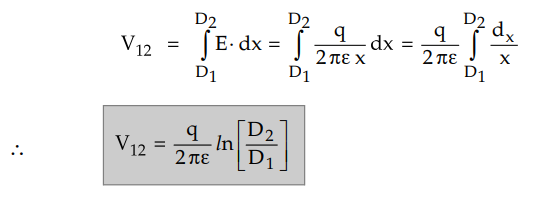
The voltage drop between two points may be either positive or negative depending upon the charge causing the potential difference is positive or negative. It also depends upon whether the voltage drop is computed from a point near the conductor to a point far away or viceversa.

Consider a system of say m conductors having radius r forming a circuit. This is shown in the Fig. 1.26.2.

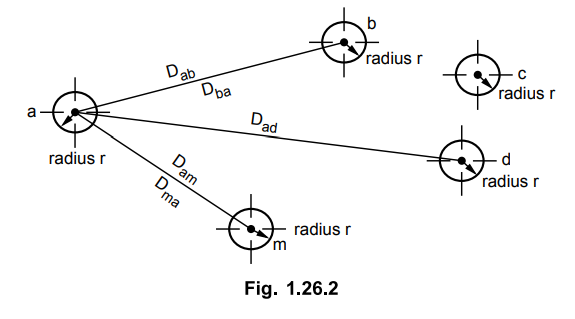
Let q_a, q_b , ... q_m be the charge in coulombs on the conductors. The spacing of conductors b, c, d ... m from conductor a is denoted by D_ab,D_ac,D_ad ... D_am are assumed to be large as compared with their radii. So the distribution of charge is uniform around the periphery of each conductor.

In order to find the potential difference between any two conductors, the principle of superposition can be used. According to this principle, the difference of potential between two charged conductors is equal to the potential difference due to charge on first conductor alone, plus the potential difference due to charge on second conductor alone, plus the potential difference due to charge on third conductor alone and so on due to other charged conductors in the field.

The potential difference between conductors a and b is given by,

V_ab = Potential difference between a and b due to charge q_a on a

+ Potential difference between a and b due to charge q_b on a

 + ... + Potential difference between a and b due to charge q_m on m

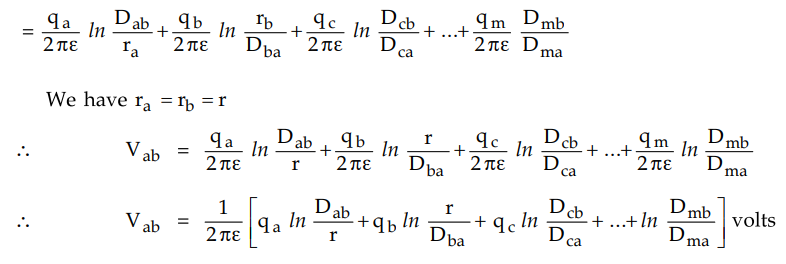
Similar expressions for the potential difference between a and other conductors can be obtained. For example

Under normal working conditions, q_a + q_b + q_c + ... + q_m = 0

The equations as obtained above will be utilized in further sections to find the capacitance per unit length of a conductor.

Review Question

1. Give an expression for potential difference between two conductors a and b in a system of m conductors.