Problems based on, to find the particular integral by the method of undetermined coefficients

Problems based on, to find the particular integral by the method of undetermined coefficients.

 

Case (a): Straight case

Example 5.5(a) (1) Solve: (D² - 3D + 2) y = 6 e^3x

Solution :

Given: y' - 3y' + 2y = 6e^3x … (1)

The auxiliary equation is m² - 3m + 2 = 0

⇒ m = 1, m = 2

(C.F) y_c = A e^x + Be^2x … (2)

Here, the solution set S = {e^x, e^2x}

R.H.S of (1) is not a member of S.

 

Example 5.5.a(2) Solve: y'' + 6y' + 5y = 2e^x + 10 e^5x

Solution :

Given: y'+6y' +5y=2ex + 10 e^5x …  (1)

The auxiliary equation is m² + 6m + 5 = 0

⇒ m = -1, m = -5

 

Example 5.5.a(3) Solve : d²y/dx² + 9y = cos 2x

Solution :

Given: y' + 9y = cos 2x … (1)

The auxiliary equation is m² + 9 = 0

⇒ m ± 3i

 (C.F) ye = A cos 3x + B sin 3x … (2)

Here, the solution set S = (cos 3x, sin 3x)

R.H.S of (1) is not a member of S.

 

Example 5.5.a(4) Solve: y" + 2y' + 4y = 13 cos (4x - 2)

Solution :

Given: y' + 2y' + 4y = 13 cos (4x-2) … (1)

The auxiliary equation is m² + 2m + 4 = 0

⇒ m = -1 ± √3 i

 

Example 5.5a(5) Solve: y" +2y' + 5y = 6 sin 3x + 7 cos 3x

Solution :

Given: y' + 2y' + 5y = 6 sin 3x + 7 cos 3x ... (1)

The auxiliary equation is m² + 2m + 5 = 0

⇒ m = -1 ± 2i

(C.F) yc = e^-x [A cos 2x + B sin 2x]

Here, the solution set S = {e^-x cos 2x, e^-x sin 2x}

R.H.S of (1) is not a member of S

Example 5.5.a(6) Solve: y" - y = e^x sin 2x

Solution :

Given: y" - y = e^x sin 2x … (1)

The auxiliary equation is m² - 1 = 0

⇒ m = ±1, i.e., m = 1, m = -1

(C.F) yc = Ae^x + Be^-x … (2)

Here, the solution set S = {e^x, e^-x}

R.H.S of (1) is not a member of S

 

Example 5.5.a(7) Solve : y" - 3y' + 2y = 4x²

Solution :

Given: y" - 3y' + 2y = 4x² … (1)

The auxiliary equation is m² - 3m + 2 = 0

⇒ m = 1, m = 2

 (C.F) y_c = A e^x + Be^2x … (2)

Here, the solution set S = {e^x, e^2x}

R.H.S of (1) is not a member of S

 

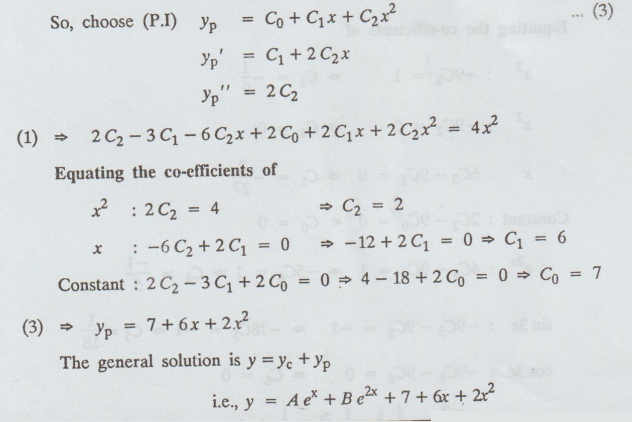
Case (b): Sum case

Example 5.5.b(1) Solve: y" - 9y = x³ + e^2x - sin 3x

Solution :

Given y" - 9y = x³ + e^2x - sin 3x

The auxiliary equation is m² - 9 = 0

⇒ m = 3, m = -3

(C.F) y_c =  A e^-3x + Be^3x

Here, the solution set S = {e^-3x, e^3x}

R.H.S. of (1) is not a member of S

 

Example 5.5.b(2) Solve: (D² - 2D + 3) y = x³ + cos x

Solution : y'' - 2y' + 3y = x³ + cos x … (1)

The auxiliary equation is m² - 2m + 3 = 0

⇒ m = 1 ± √2 i

 

Example 5.5.b(3) Solve : d2y/dx2 + dy/dx – 2y = x + sin x

Solution :

Given: y'' + y' - 2y = x + sin x … (1)

The auxiliary equation is m² + m - 2 = 0

⇒ m = 1, m = -2

(C.F) y_c = Ae^x + Be^-2x

Here, the solution set S = {e^x, e ^-2x}

R.H.S of (1) is not a member of S.

 

Example 5.5.b(4) Solve (D2 + 3D + 2) y = 4e2x + x by using the method of undetermined coefficients.

[A.U N/D 2019 R-17]

Solution: Given: y'' + 3y' + 2y = 4 e^2x + x ... (1)

The auxiliary equation is m² + 3m + 2 = 0

⇒ m = -1, m = -2

 

Case (c) : Modified Case :

Example 5.5.c(1) Solve : d²y / dx² – 5 dy/dx + 6y = e^3x + sin x

Solution :

Given: y" - 5y' + 6y = e^3x + sin x … (1)

The auxiliary equation is m² - 5m + 6 = 0 ⇒ m = 3, m = 2

(C.F) ye Ae^2x + Be^3x... (2)

Here, the solution set S = {e2x, e^3x}

Normaly we choose (P.I) y_p = C₁e^3x + C₂ sin x + C₃ cos x

First term in R.H.S of (1) is a member of S.

Here, the corresponding term should be multiplied by x

 

Example 5.5.c(2) Solve (D² + 2D + 1) y = e^x sin 2x by using the method of undetermined co-efficients.

[A.U A/M 2019 R-17]

Solution: Given: (D² + 2D + 1)y = e^x sin 2x

The auxiliary equation is m² + 2m + 1 = 0

⇒ (m + 1)² = 0

⇒ m = -1,-1

 

Example 5.5.c(3). Solve (D - 2)³y = 17 e^2x

Solution :

Given: (D − 2)³ y = 17 e^2x

 

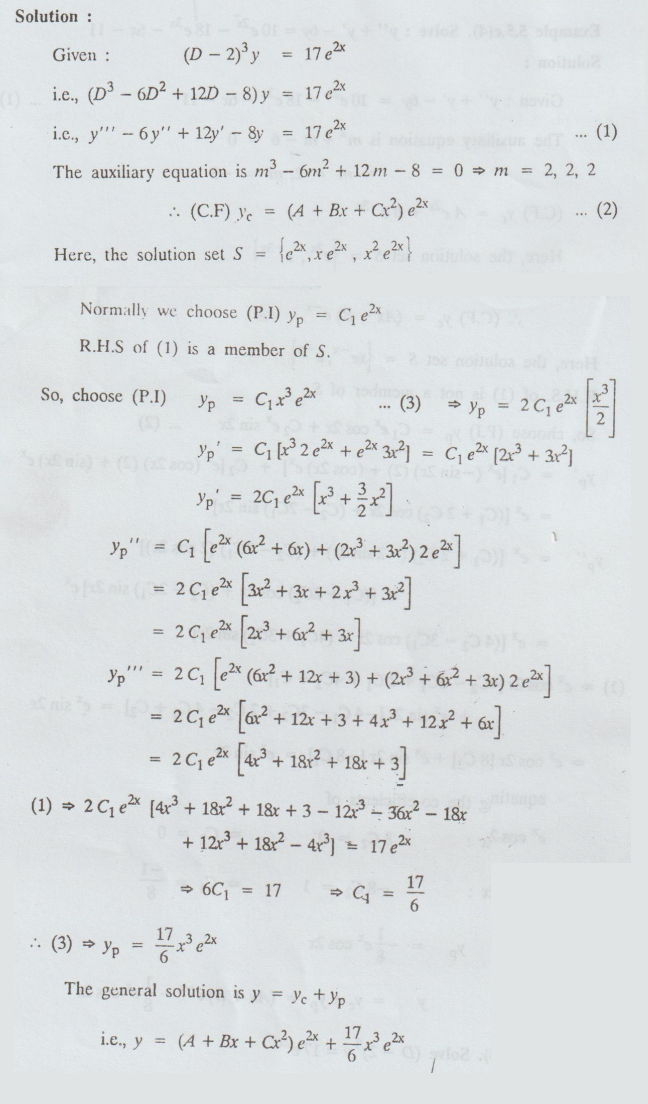
Example 5.5.c(4). Solve : y'' + y' - 6y = 10 e^2x - 18 e^3x - 6x – 11

Solution :

Given: y'' + y' - 6y = 10 e^2x - 18 e^3x - 6x – 11 … (1)

The auxiliary equation is m² + m - 6 = 0

⇒ m = 2, m = -3