Problems based on system of simultaneous linear differential equations with constant co-efficients

IV. PROBLEMS BASED ON SYSTEM OF SIMULTANEOUS LINEAR DIFFERENTIAL EQUATIONS WITH CONSTANT CO-EFFICIENTS.

 

TYPE 1:

Example 5.4.1. Solve dx / dt - y = 0, dy / dt + x = 0

[A.U. A/M. 2008]

Solution:

Given:

Dx - y = 0 ... (1)

Dy + x = 0 … (2)

 (1) × D ⇒  D² x – Dy = 0 … (3)

(2) × 1 ⇒ Dy + x = 0 … (4)

(3) + (4) ⇒ D² x + x = 0

(D² + 1) x = 0

The auxiliary equation is m2 + 1 = 0

m² = -1  m = ± i

x = A cost + B sin t

dx / dt = -A sint + B cost

Given: dx/dt - y = 0⇒ y = dx / dt

⇒ y = -A sint + B cost

 

Example 5.4.2 Solve dx / dt + y = e^t, x – dy / dt = t  [A.U N/D 2012, N/D 2014 R13]

Solution:

 

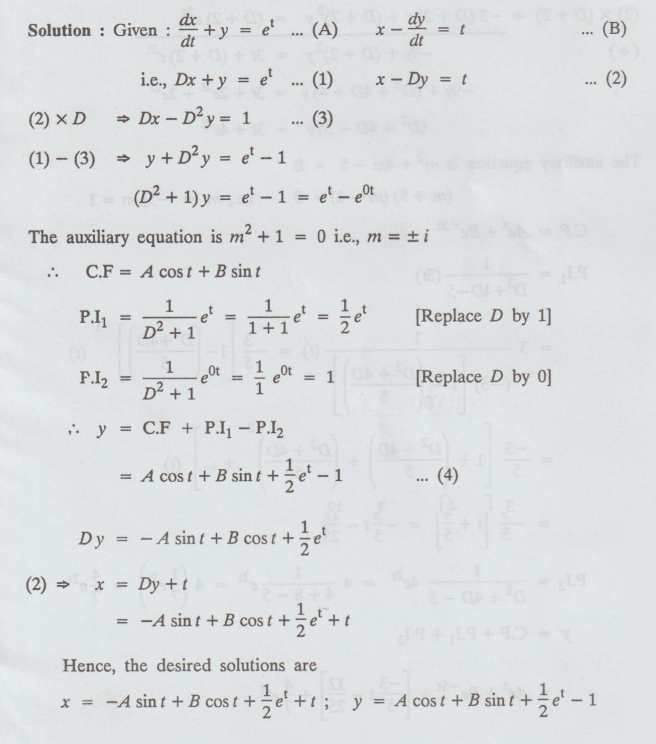
Example 5.4.3. Solve dx/dt + 2x - 3y = t ; dy/dt -3x + 2y = e^2t

 [A.U. N/D 2007, M/J 2008] [A.U N/D 2016 R-8] [A.U M/J 2016 R8]

Solution:

 

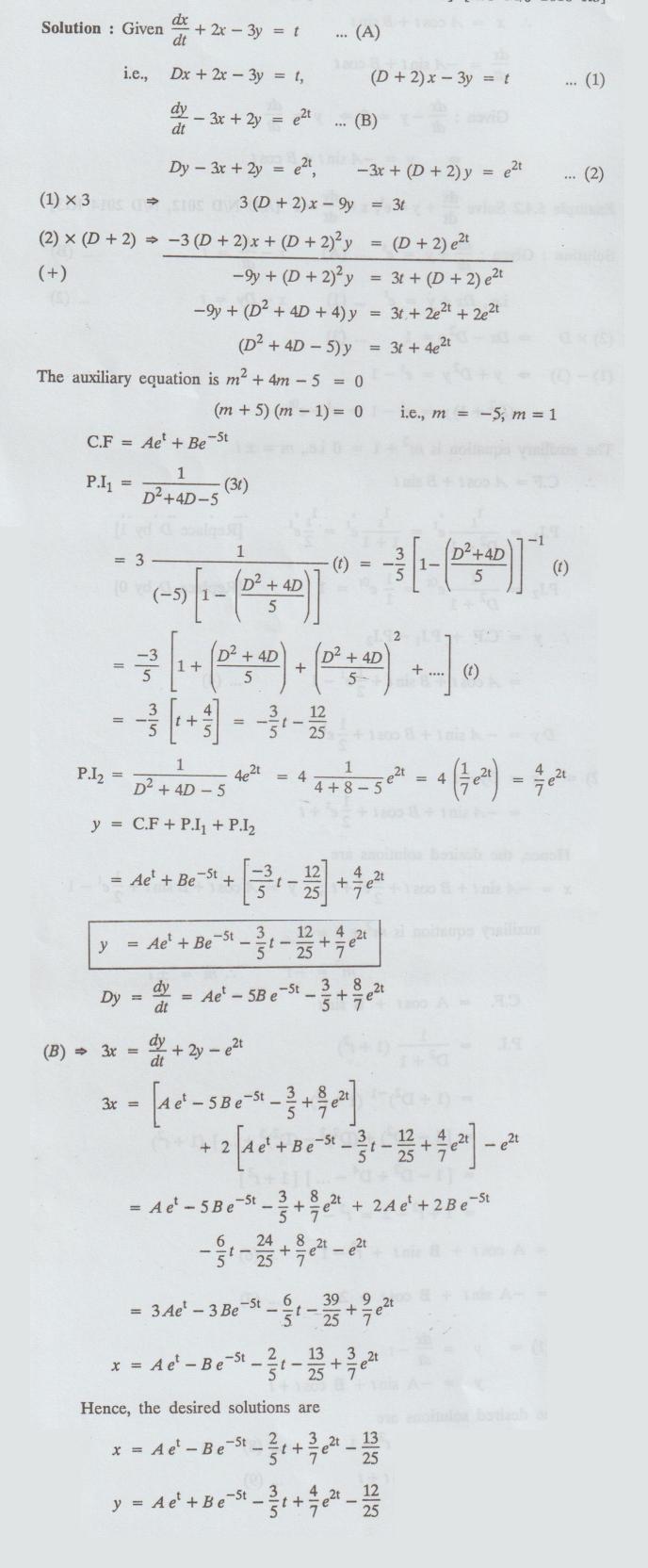
Example 5.4.4. Solve : dx/dt – y = t; dy/dt + x = t² ; Given x (0) = y (0) = 2

 [A.U. N/D 2003, N/D 2011, A/M 2011] [A.U M/J 2016 R-13]

Solution: Given: dx/dt - y = t dy / dt + x = t²

 

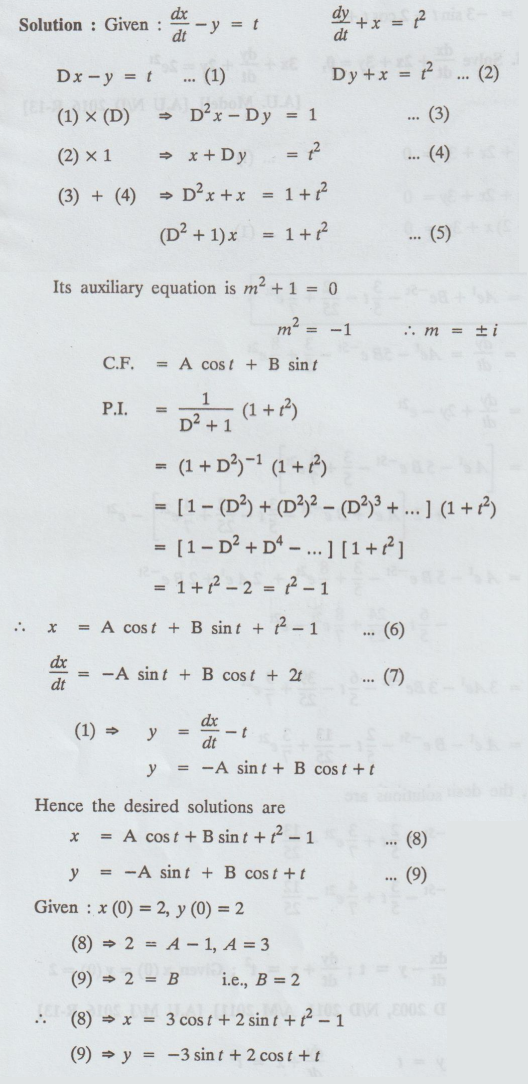
Example 5.4.5. Solve dx/dt + 2x + 3y = 0, 3x + dy/dt + 2y = 2e^2t

 [A.U. Model] [A.U N/D 2016 R-13]

Solution :

 

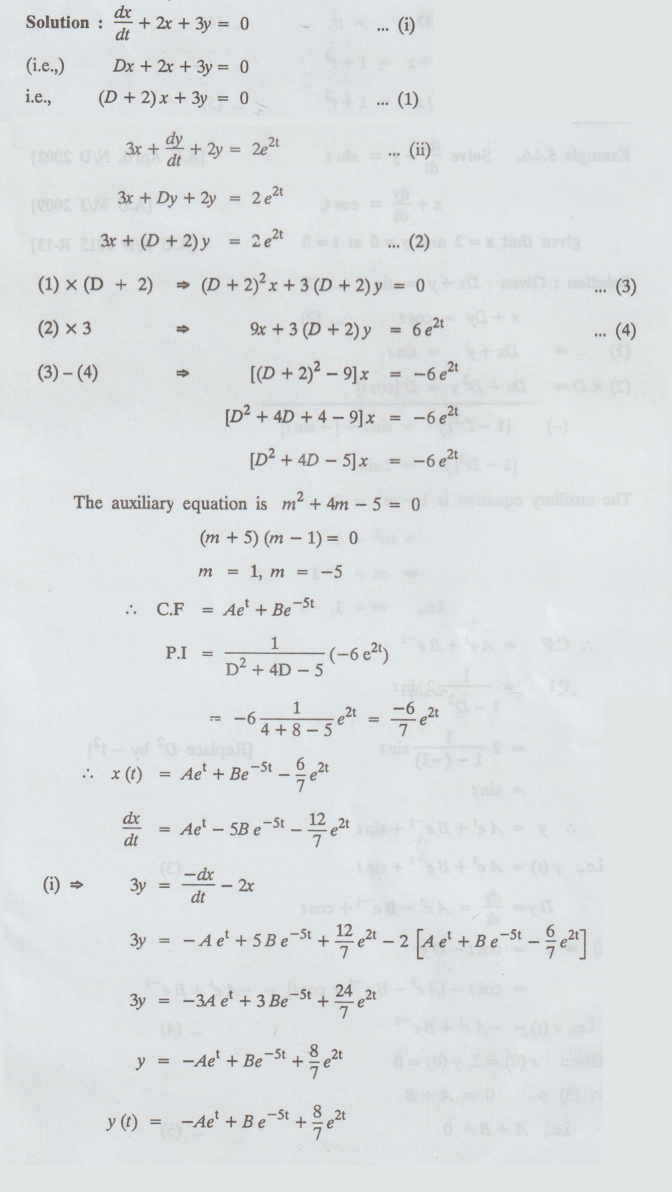
Example 5.4.6. Solve dx / dt + y = sin t

given that x = 2 and y = 0 at t = 0

[A.U April, N/D 2002]

[A.U M/J 2009]

[A.U N/D 2015 R-13]

Solution: Given: Dx + y = sin t ... (1)

x + Dy = cos t ... (2)

 

Example 5.4.7. Solve dx/dt + 2y = -sint, dy/dt – 2x = cos t given x = 1 and

[A.U. N/D 2010] [A.U M/J 2014 R-13]

[A.U. A/M 2017 R-8] [A.U D2015/Jan.16 R-8]

Solution:

 

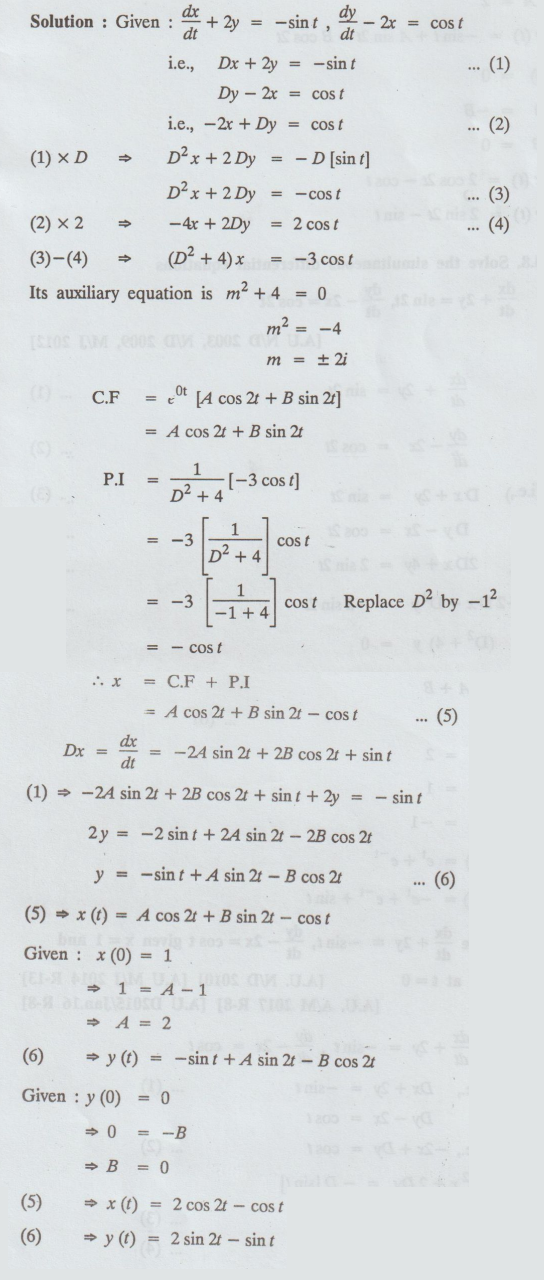
Example 5.4.8. Solve the simultaneous differential equations

dx/dt + 2y = sin, dy/dt – 2x = cos 2t

 [A.U N/D 2003, N/D 2009, M/J 2012]

Solution :

 

Example 5.4.9. Solve the simultaneous equations.

dx / dt + 2x + 3y = 2e^2t; dy/dt + 3x + 2y = 0

 [A.U. April/May 2003] [A.U A/M 2003, M/J 2010] [A.U. A/M 2017 R-13]

Solution :

 

Example 5.4.10. Solve dx/dt + 2y 5e^t and dy/dt - 2x = 5e^t = 5e' given that x = -1 and y = 3 at t = 0.

Solution :

 

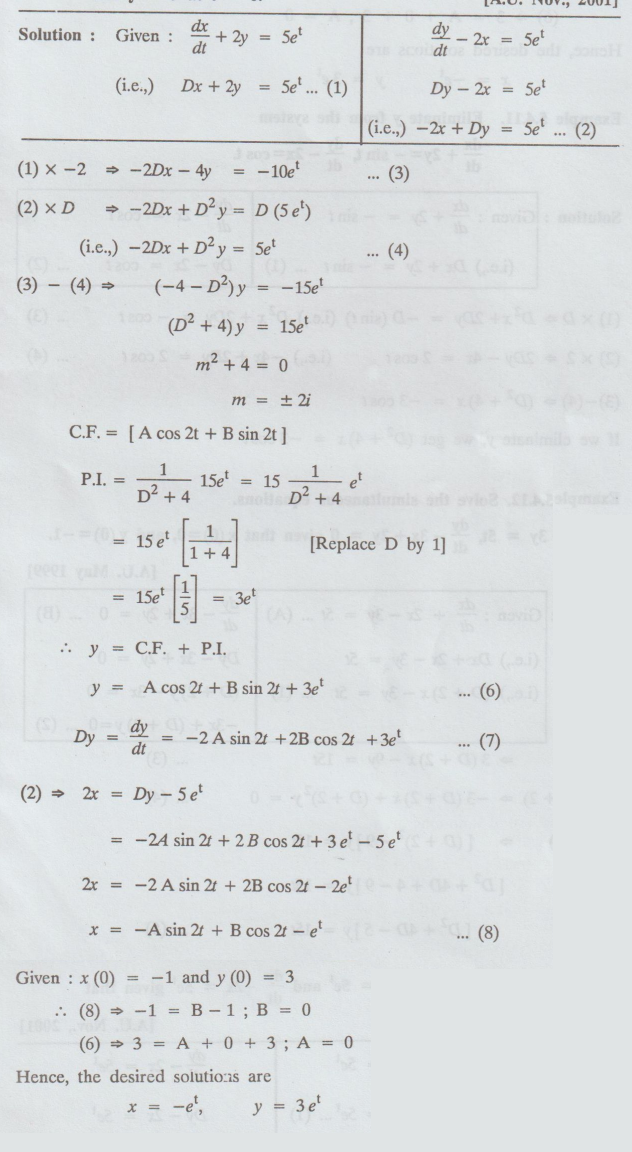
Example 5.4.11. Eliminate y from the system

dx/dt + 2y = - sin t, dy/dt - 2x= cos t.

Solution:

 

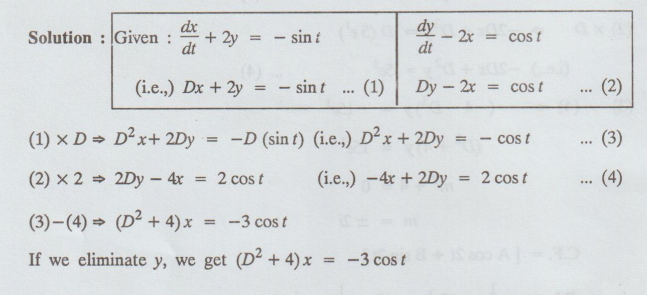
Example 5.4.12. Solve the simultaneous equations.

dx/dt + 2x - 3y = 5t, dy/dt - 3x + 2y = 0 given that x (0) = 0, and y (0) = -1.

Solution:

 

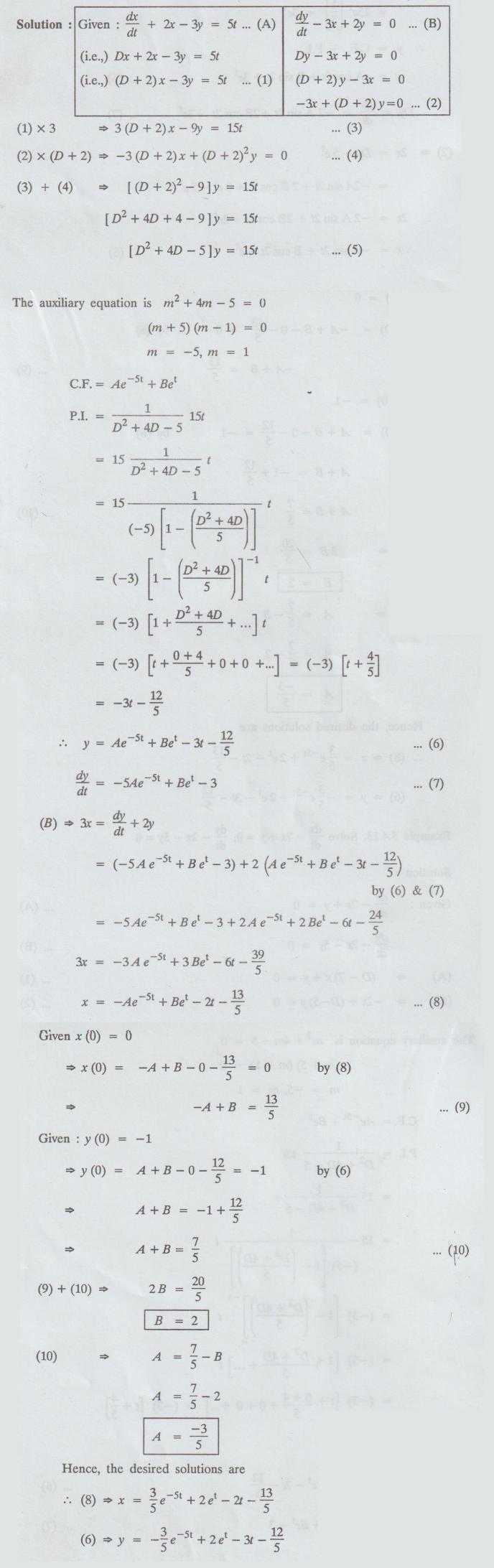
Example 5.4.13. Solve dx/dt  - 7x + y = 0, dy/dt - 2x - 5y = 0

Solution :

TYPE II.

Example 5.4.14. Solve the simultaneous differential equations :

dx/dt + dy/dt + 3x = sin t, dx/dt + y – x = cos t

 [A.U A/M 2015 R-13] [A.U A/M 2019 R-17]

Solution:

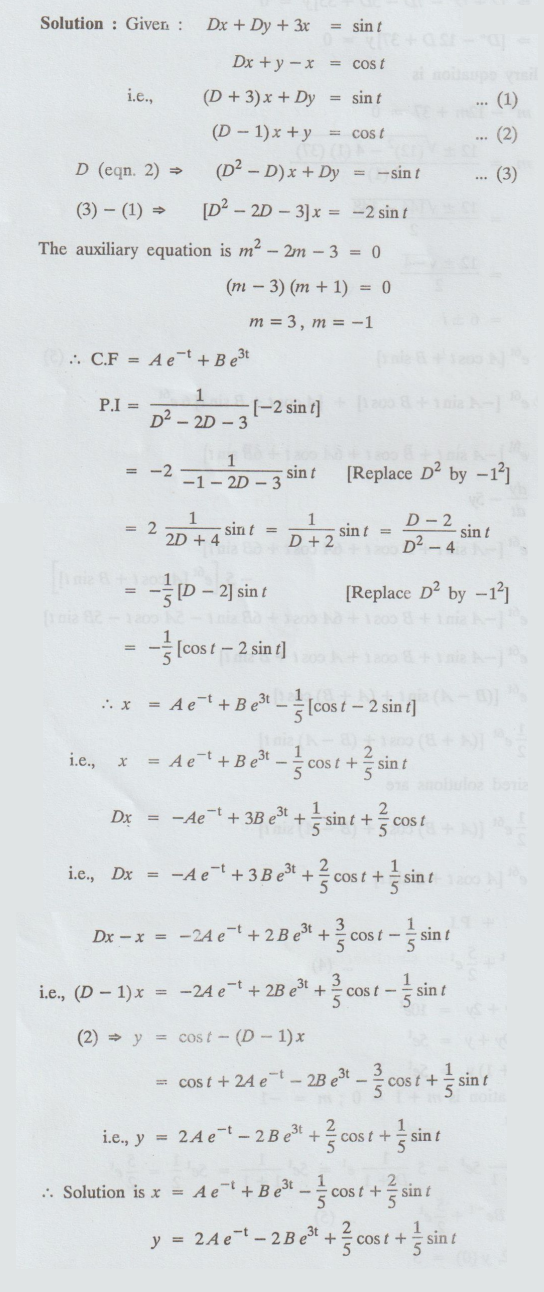
Type III

Example 5.4.15. Solve dx/dt + dy/dt + x + y = 10 e^t

Solution :

Note : Consider the determinant coefficient of the simultaneous equations

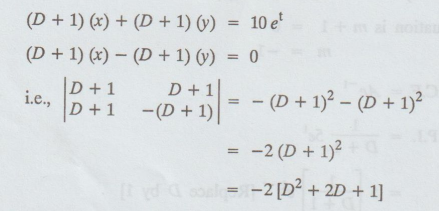
Here, the degree of D is 2. So, the solutions for x and y should contain two independent arbitrary constants.

This is a special problem in which we get the solution for x contains only one arbitrary constant A and the solution for y also contains, only one arbitrary constant B. Infact, both A and B are two independent arbitrary constants because we cannot express here, A in terms of B or B in terms of A. Always, we need not expect both the solutions for x and y to contain two arbitrary constants A and B.

 

Example 5.4.16. Solve the system of equation

(D + 1) x + (2D + 1) y = e^t

(D-1) x - (D + 1) y = 1

Solution: