R.M.S (root mean square) value or effective value

R.M.S (ROOT MEAN SQUARE) VALUE OR EFFECTIVE VALUE

Definition

The steady current which when flowing through a given resistor for a given time produces the same amount of heat as produced by the alternating current when flowing through the same resistor for the same time is called R.M.S. or effective value of the alternating current.

Thus for defining R.M.S value, the heating effects of A.C. and D.C. are compared.

1. To Find R.M.S Value

Method 1 [Mid-ordinate Method]

Let the wave form of the alternating current be as shown in the figure. Let the current of this wave form flow through a resistor R ohms for time t seconds.

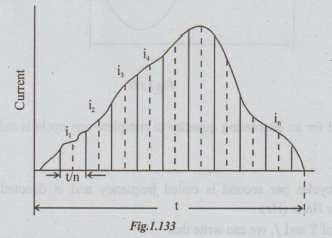
Divide the time base t into n equal intervals of time, each of duration t/n seconds. Let the average values of instantaneous currents during these intervals be i, iz..., in as shown in the figure. They are also called mid-ordinates. As a result of current flow, heat is produced.

Heat produced in first interval

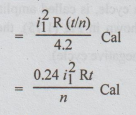
Heat produced in second interval

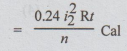
Heat produced in n^th interval

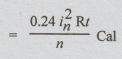
Hence, total heat produced in t seconds

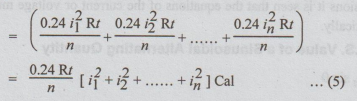
Suppose that a direct current of I pass through the same resistor for the same time t.

The heat produced by I = 0.241²Rt ... (6)

If I be the effective value of the A.C. current then heat produced by I = total heat produced by the alternating current. Equating equations (5) and (6), we get,

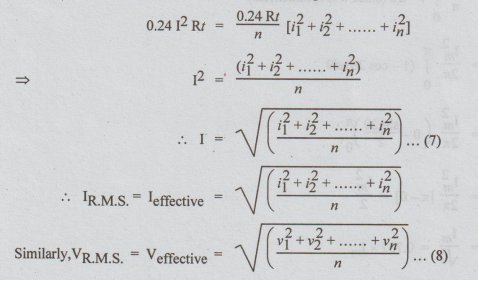
Note:

1. The name R.M.S. has come from the expression for R.M.S. value given by equation (7).

2. This method can be applied for both symmetrical and unsymmetrical wave forms. It is mainly useful for the wave forms whose equations will be complicated.

3. For irregular shape waveforms, the result will be more accurate if we take more intervals.

Methods 2: (Analytical method)

For unsymmetrical wave forms.

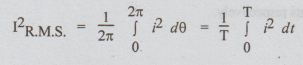
For symmetrical wave forms.

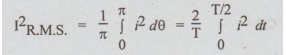
From the above expressions it is seen that the equations of the current or voltage must be known to find the R.M.S value analytically.

2. To find the R.M.S. Value of a Sinusoidal Alternating Quantity

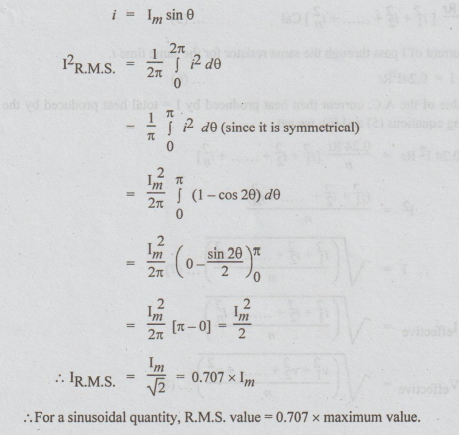
Note:

1. In electrical engineering unless otherwise stated the given a.c. voltage and current must be treated as R.M.S. values.

Suppose we say the supply voltage in house is 230 volts, it means that the R.M.S value of the supply voltage is 230 volts.

2. The suffix R.M.S. or effective is only optional. We can denote R.M.S value of current as I instead of IR.M.S or leffective. Similarly, we can denote R.M.S. value of voltage by V instead of VR.M.S or Veffective

3. Sometimes we can denote R.M.S value of voltage by E. As a whole, we use V(or E) and I for R.M.S. values of A.C. voltages and currents respectively.

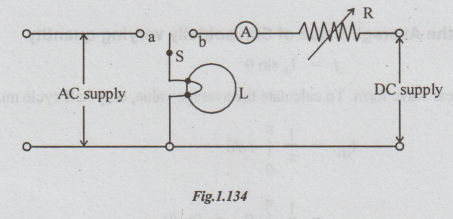
3. To illustrate the Significance of R.M.S. Value of an Alternating Current

Refer the figure below. L is the metal filament lamp connected to an A.C. supply by closing the switch S onto the position a. The brightness of the filament is noted. Now, the switch S is moved to position b and the resistance of the rheostat R is adjusted to give the same brightness. The reading on the moving coil ammeter A gives the value of direct current that produces the same heating effect as that produced by the alternating current (i.e.,) the reading of the ammeter gives the R.M.S. value of the A.C. current. For example, if ammeter reading is 0.5A then we say that the R.M.S. value of the alternating current is 0.5A.

Note

The R.M.S value of a given alternating quantity can also be found graphically by the following formula:.

R.M.S. value = √(Area of the squared wave / base)