Relaxation Time

Relaxation Time

• The medium is called homogeneous when the physical characteristics of the medium do not vary from point to point but remain same everywhere throughout the medium. If the characteristics vary from point to point, the medium is called nonhomogeneous or heterogeneous. While the medium is called linear with respect to the electric field if the flux density  is directly proportional to the electric field   . The relationship is through the permittivity of the medium. If  is not directly proportional to , the material is called nonlinear.

Consider a conducting material which is linear and homogeneous. The current density for such a material is,

The point form of the continuity equation states that,

• This is a differential equation in ρv whose solution is given by,              

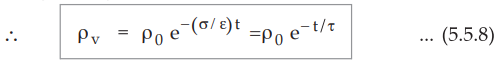
where  p0 = Charge density at (t = 0)

• This shows that if there is a temporary imbalance of electrons inside the given material, the charge density decays exponentially with a time constant τ = Ɛ / σ sec. This time is called relaxation time.

• The relaxation time (τ) is defined as the time required by the charge density to decay to 36.8 % of its initial value.

τ = Relaxation time = Ɛ / σ sec …. (5.5.9)

• For a pure conductor, the r is very very small, of the order of 10^-19 sec and thus for any imbalance inside the conductor, the charge density reduces to zero very quickly, forcing the electrons causing imbalance, to the surface of the conductor.

Key Point : This shows that under static conditions no free charge can remain within the conductor and it gets evenly distributed over the surface of the conductor.

Ex. 5.5.1 Determine the relaxation time for silver, having n = 6.17 × 10⁷ mho/m. If charge of density p 0 is placed within a silver block, find the charge density after one time constant and five time constants. Assume Ɛ = Ɛ0.

Sol. :

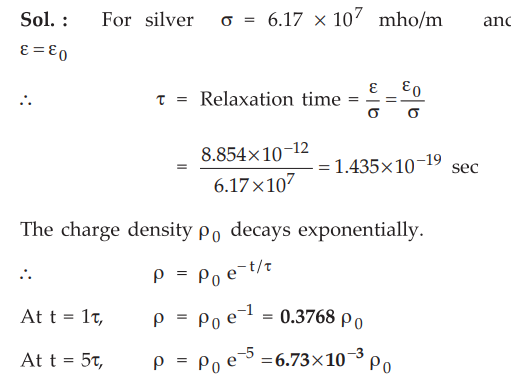
Review Question

1. What is relaxation time ? Derive expression for it.