Representation of sinusoidal quantities in polar form- drawing the phasors

REPRESENTATION OF SINUSOIDAL QUANTITIES IN POLAR FORM- DRAWING THE PHASORS

Case (a): Consider I = I_m sin ωt

Its maximum value = I_m

Its effective value (RMS value) = | I | = I_m/√2 = 0.707 I_m

ωt is taken as reference angle (zero angle). In the polar form, any quantity is shown in the following way.

The phasor (vector) = | Magnitude| ∠ angle with reference to reference.

Here, I = | I | ∠ 0

This phasor is shown along positive x-axis as below.

Case (b): Consider i = Im sin (ωt + ɑ)

In the polar form, I = |I| ∠ ɑ

This phasor makes an angle a with reference (positive x-axis) in the anti-clockwise direction (above positive x-axis).

This is illustrated as below.

Case (c): Consider

In the polar form, we write

I = | I | ∠ - β

This phasor is shown below reference axis by angle β.

The above equations can be shown as phasors as shown hereunder

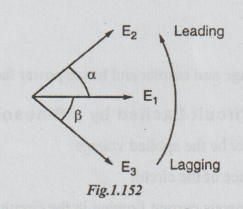
Taking E, as reference, we can say that E₂ leads E₁ by ɑ and

E₃ lags behind E₁ by β.

- angle indicates lagging and + angle indicates leading.

Suppose that we want to explain the phase relation between E2 and E3, it is done as explained below.

The angle between E₂ and E₂ is (ɑ + β). The arrow is given in the anti-clockwise direction. The arrow side quantity is E₂. Hence we say that E2 leads E₃ by angle (ɑ + β). It is as good as saying that E3 lags behind E2 by same angle (ɑ + β).

This arrow can be used for expressing the phasor relation between E₁ and E₂ and also between E₁ and E₃

Taking E₁ as reference, we can say that E₂ leads E1 by ɑ and

E₃ lags behind E₁ by β .

- angle indicates lagging and + angle indicates leading.

Suppose that we want to explain the phase relation between E₂ and E₃, it is done as explained below.

The angle between E₂ and E₃ is (ɑ + β ). The arrow is given in the anti-clockwise direction. The arrow side quantity is E₂. Hence we say that E₂ leads E₃ by angle (ɑ + β). It is as good as saying that E₃ lags behind E₂ by same angle (ɑ + β).

This arrow can be used for expressing the phasor relation between E, and E2 and also between E₁ and E₃.