Sequence Detector

Sequence Detector

• The specified input sequence can be detected using a sequential machine called sequence detector. In this circuit output goes high when a prescribed input sequence occurs. A typical input sequence and the corresponding output sequence for desired input sequence 101 are :

 

Step 4 : K-map simplification

Step 5 : Logic diagram

• As shown above the detection of required input sequence can occur in a longer data string and the desired input sequence can overlap with another input sequence. It is assumed that input can change only between clock pulses. Once we know the sequence which is to be detected, we can draw the state diagram for it. Then from the state diagram we can design the circuit. It is possible to implement sequence detector using both types of sequential machines Mealy machine and Moore machine. The following examples illustrate how to determine the state diagram from the given input sequence and then implement the sequence detector. Illustrative Examples

 

Illustrative Examples

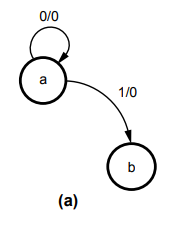
Ex. 5.10.1 Design a Mealy type sequence detector to detect a serial input sequence of 101.

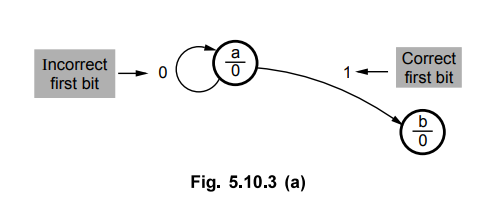
Sol. : In a Mealy type design, the number of states in the state diagram are equal to the number of bits in the desired input sequence. In this example, we have three bits in the sequence so we have three states in the state diagram. Once the number of states are known we have to draw the direction lines with states of inputs and outputs. Let us start drawing direction lines, assuming state 'a' as an initial state.

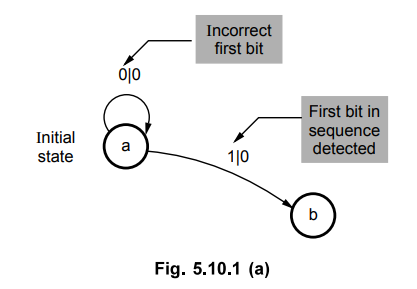
1. State a

State a checks for 1. When input is 1, we have detected the first bit in the sequence, hence we have to go to the next state to detect the next bit in the sequence.

When input is 0, we have to remain in the state 'a' because bit 0 is not the first bit in the sequence. In both cases output is 0 since we have not yet detected all the bits in the sequence.

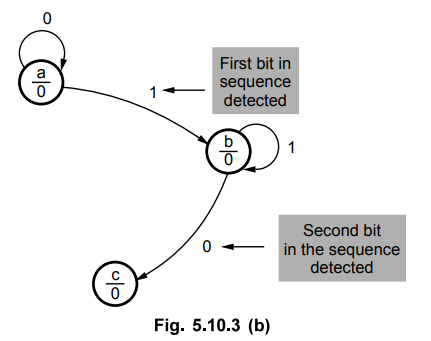
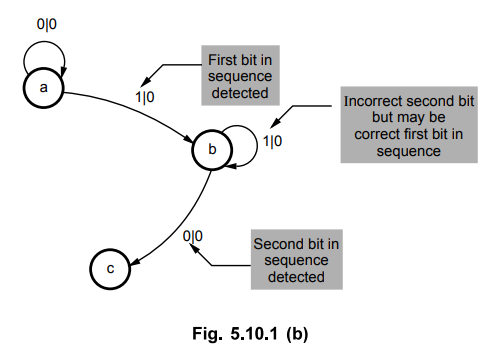
2. State b

When input is 0, we have detected the second bit in the sequence, hence we have to go to the next state to detect the next bit in the sequence. When input is 1, we have to remain in state b because 1 which we have detected may start the sequence. Output is still zero.

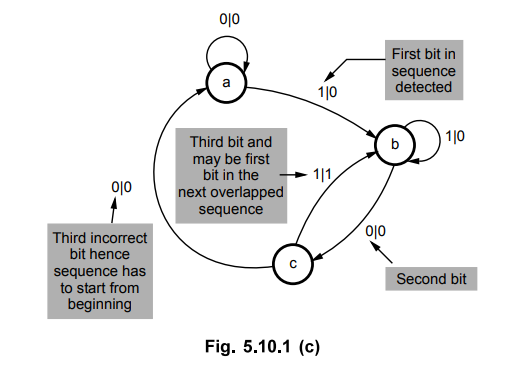
3. State c

As explained for state a and state b, if desired bit is detected we have to go for next state otherwise we have to go to the previous state from where we can continue the desired sequence. When complete sequence is detected we have to make output HIGH and go to the initial state. This is illustrated in Fig. 5.10.1 (c).

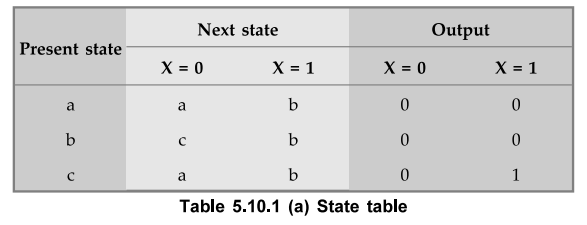
From the above state diagram we can determine the state table as shown in Table 5.10.1 (a).

 

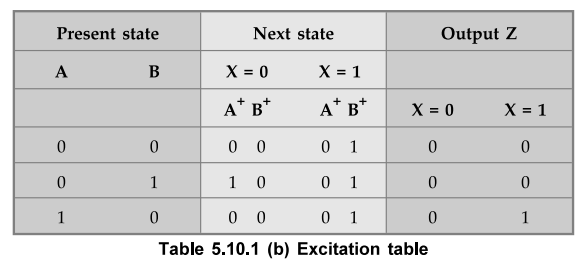
Since there are three states we need two flip-flops. Assigning state a = 00, state b = 01 and state c = 10 we can determine the excitation table as shown in Table 5.10.1 (b).

K - map simplification

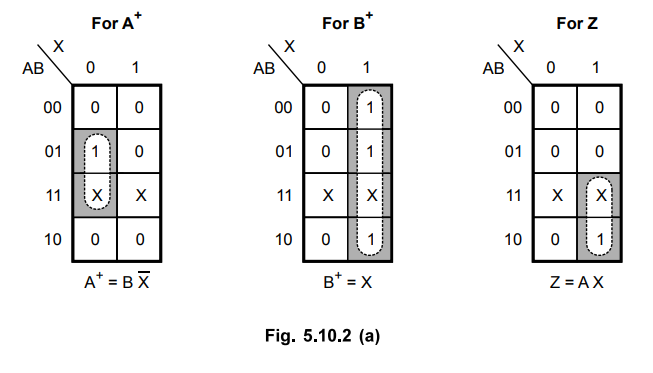
Logic diagram

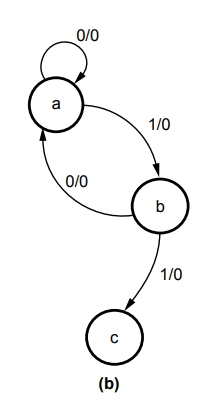
Ex. 5.10.2 Design a Moore type sequence detector to detect a serial input sequence of 101.

Sol. : In a Moore type design output depends only on flip-flop states. Therefore, in the state diagram of Moore machine, the output is written with the state instead of with the transition between the states. Apart from this the process of determining the state diagram is similar to that used for Mealy machine. Let us start with state 'a' as an initial state.

1. State a

When input is 1, we have detected the first bit in the sequence, hence we have to go to the next state to detect the next bit in the sequence.

When input is 0, we have to remain in the state 'a' because bit 0 is not the first bit in the sequence. In both cases output is 0 since we have not yet detected all the bits in the sequence.

2. State b

When input is 0, we have detected the second bit in the sequence, hence we have to go to the next state to detect the next bit in the sequence. When input is 1, we have to remain in state b because 1 which we have detected may start the sequence. Output is still zero.

3. State c

Now, when a 1 input occurs, the 101 sequence is completed and output must equal to 1. Here, we cannot go back to state b (since output in state b is zero) and hence we have to create new state d with a output 1.

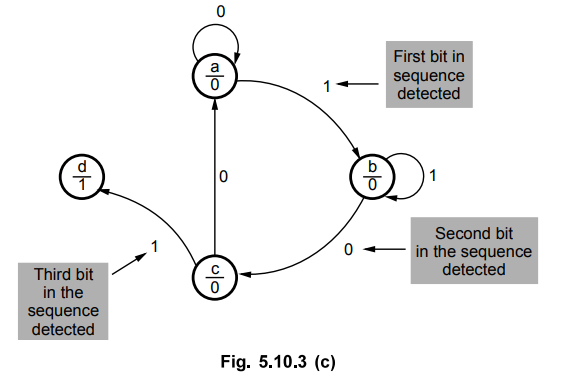
In case if input is zero, we have to restart checking of input sequence and hence we have to return to state a.

4. State d

Since the sequence is detected, this is the last state. When input is 1, we have detected the first bit in the next sequence, hence we have to go to state b.

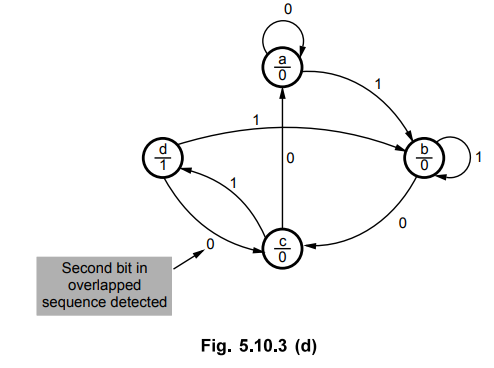
When input is 0, we have detected the second bit in the overlapped sequence, hence we have to go to state c.

From the above state diagram we can determine the state table as shown in Table 5.10.2 (a).

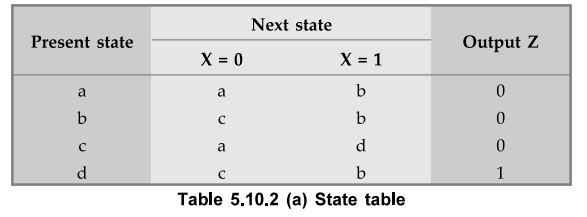
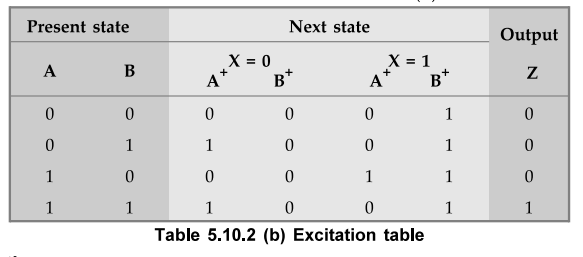
Since there are four states we need two flip-flops. Assigning state a = 00, b = 01, c = 10 and d = 11 we can determine the excitation table as shown in Table 5.10.2 (b).

K - map simplification

 

 Logic diagram

Examples with Solutions

Ex. 5.10.3 Design a sequence detector to detect the following sequence using JK flip-flops. (Use Mealy Machine) ... 110

Sol. : The given sequence has 3-bit, so we require 3 states in the state diagram. Let us start drawing direction lines, assuming state 'a' is an initial state.

State a :

When input is 1, we have detected the first bit in the sequence, hence we have to go to the next state to detect the next bit in the sequence. When input is 0, we have to remain in the state 'a' because bit 0 is not the first bit in the sequence. In both cases output is 0, since we have not yet detected all the bits in the sequence.

State b :

When input is 1, we have detected the second bit in the sequence, hence we have to go to the next state to detect the next bit in the sequence. When input is 0, we have to go to the state 'a' to detect the first bit in the sequence, i.e. 1.

State c :

When input is 0, we have detected the last bit in the sequence, hence we have to go to the initial state, to detect the next sequence and make output high indicating sequence is detected. When input is 1, we have to go to the state 'b' because 1 which we have detected may start the sequence.

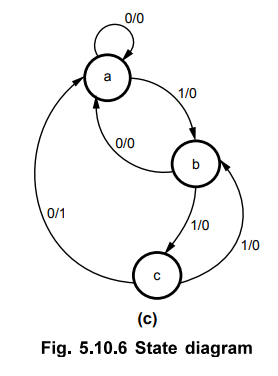
Assuming state assignments as a = 00, b = 01 and c = 10, we can determine excitation table for above state diagram as shown in Table 5.10.3.

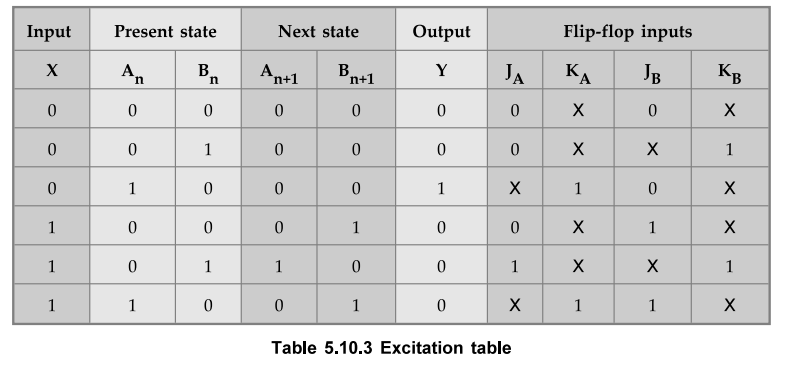
K-map simplification

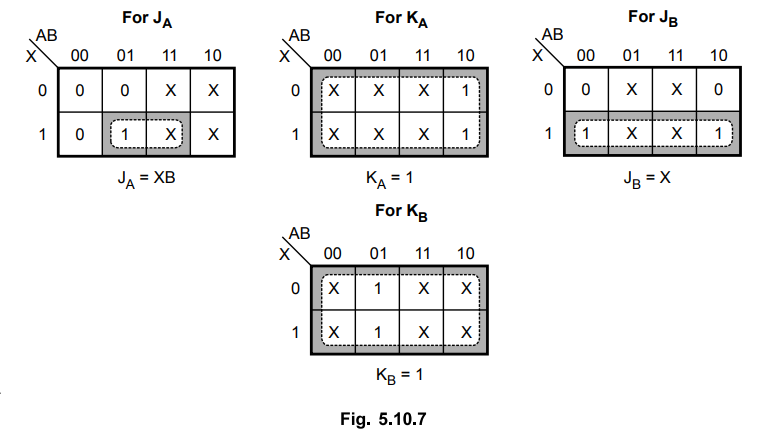
 Logic diagram

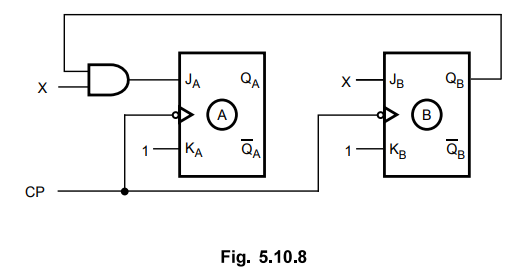
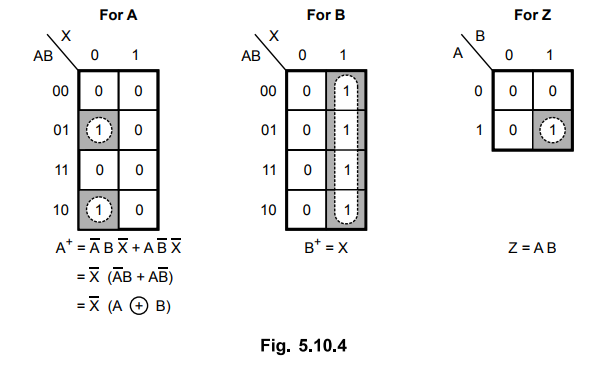
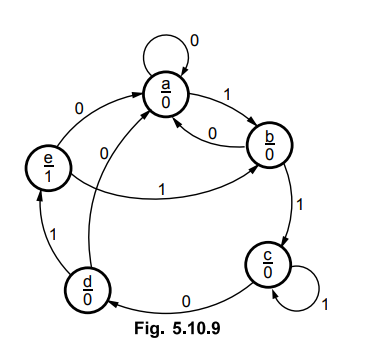
Ex. 5.10.4 Design a sequence detector to detect sequence 1101.

Sol. : State diagram

In Moore model, output depends only on the present state and not on the input, so state diagram is as shown in the Fig. 5.10.9.

State table

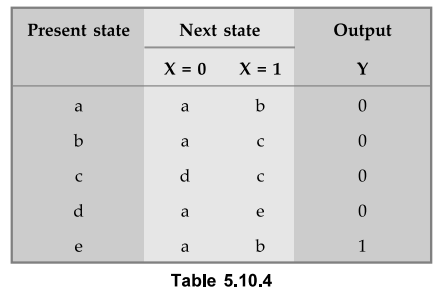
State assignment

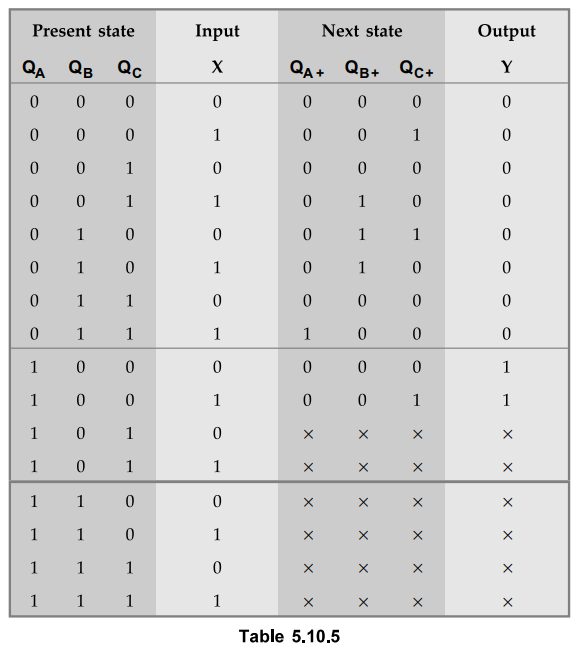
a = 000, b = 001, c = 010, d = 011 and e = 100

State transition table

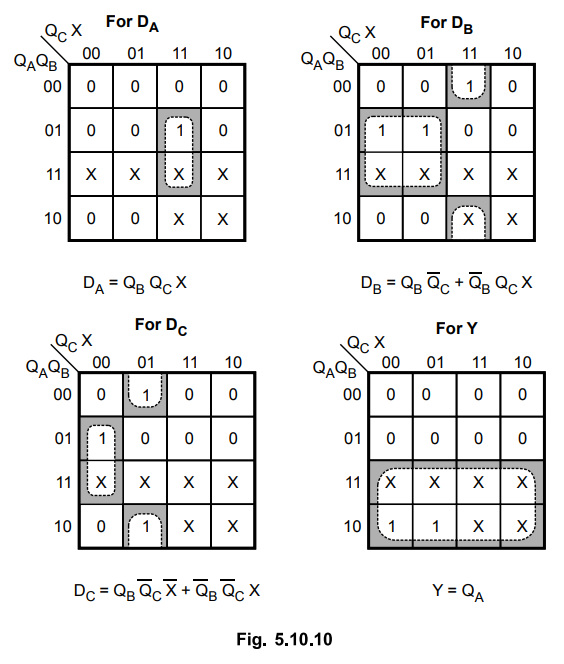
K-map simplification

 Logic diagram

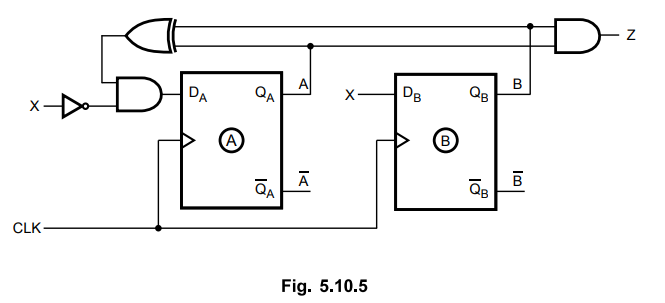
Ex. 5.10.5 Design a Mealy model of sequence detector to detect the pattern 1001.

Sol. :

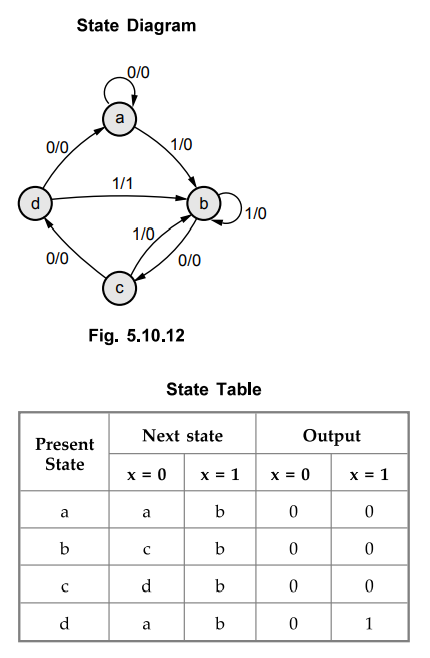
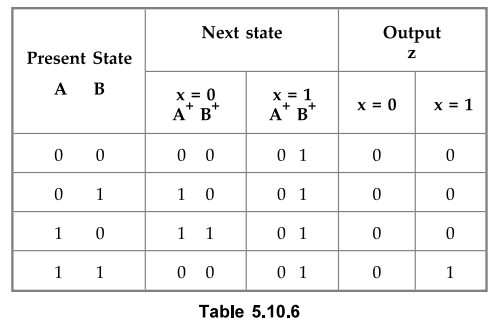
Assigning state a = 00, b = 01, c = 10 and d = 11 we have

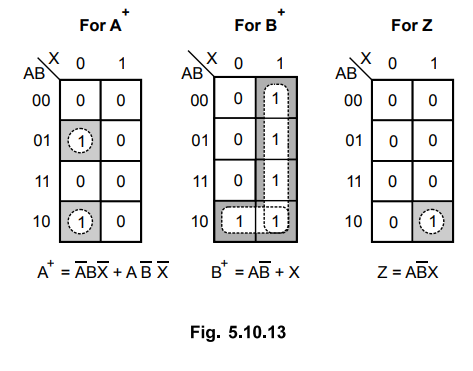
K-map Simplification

 

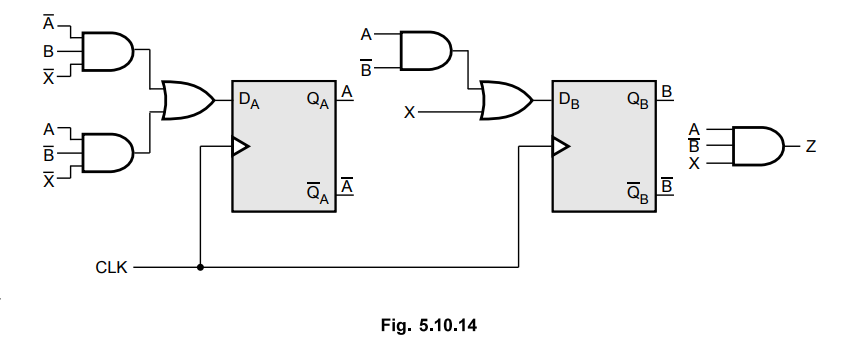
Logic diagram

 

 

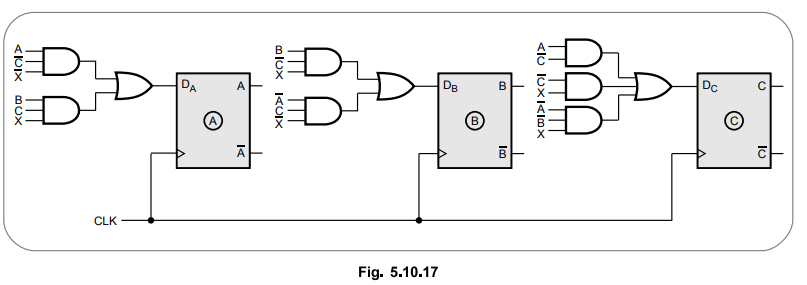
Ex. 5.10.6 Design a sequence detector that produces an output 'J' wherever the non - overlapping sequence 101101 is detected.

AU : Dec.-16, Marks 13

Sol. : State diagram

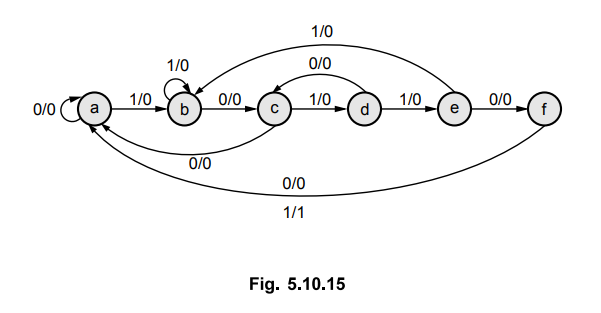
State Table

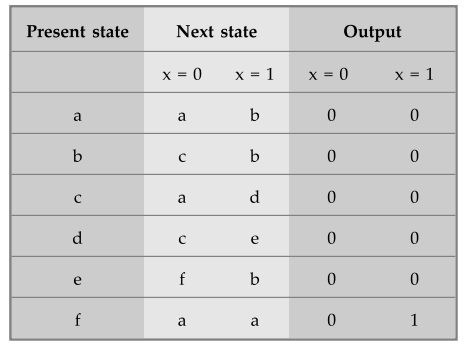
State assignment

a = 000, b = 001, c = 010, d = Oil, e = 100, f = 101

State transition table

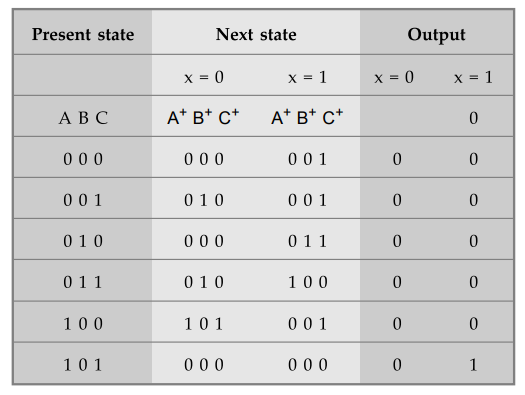
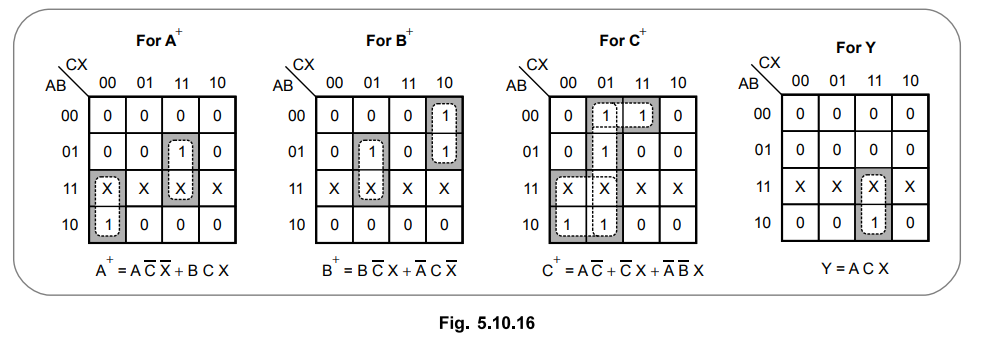
K - map simplification - using D flip - flops

Logic diagram

Example for Practice

Ex. 5.10.7 Design a sequence detector which detects the sequence "OHIO" using D flipflops (one bit overlapping).

AU : Dec.-12, Marks 8