Short Questions and Answers

SHORT QUESTIONS AND ANSWERS

 

1. Write the sufficient condition for Gauss-Seidel method and Gauss-Jacobi method to be converge. [AU A/M 2018 R08, R13SNM] [A.U A/M 2019 (R17)] [A.U N/D 2020 (R17), A/M 2021 (R17)]

Solution:

The coefficient of matrix should be diagonally dominant.

 

2. Gauss elimination and Gauss-Jordan are direct methods while and ....... are iterative methods.

Solution:

(i) Gauss-Seidel method; (ii) Gauss-Jacobi method no

 

3. Give two indirect methods to solve a system of linear equations. [M.U. April, 2001]

Solution: (i) Gauss-Jacobi method; (ii) Gauss-Seidel method

 

4. Solve the system of equations

2x-3y+20z = 25

20x + y 2z = 17

3x+20y - z = -18 by Gauss-Jacobi iteration method.

[Only two iteration]

[A.U. Nov. 1996]

Solution: As the coefficient matrix is not diagonally dominant as it is, we rewrite the equation.

20x + y 2z = 17; 3x + 20yz = -18; 2x - 3y + 20z = 25

Now, the diagonal elements are dominant in the coefficient matrix, we write x,y,z as follows :

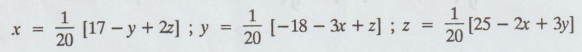
Let the initial conditions be x = 0, y = 0, z = 0

First Iteration :

Second iteration :

 

5. Compare Gauss-elimination and Gauss-Seidel methods.

 (or)

[A.U CBT A/M 2011]

State the merits and demerits of elimination methods and iterative methods for solving a system of equations.

Solution :

Gauss elimination method

1. It works on the basis of elimination of variables

2. These can be used for small number of co-efficients.

3. Its performance is affected due to  round-off errors.

4. Direct method for solving linear simultaneous equations.

5. It gives the exact solution in finite number of steps.

Gauss-Seidal method

1. It employs initial values and iterates to obtain refined estimates.

2. These can be used for large number of co-efficients.

3. There is no round-off error problem. Error is controlled by number of iterations.

4. Iterative method for solving linear simultaneous equations.

5. Successive approximations get the solution.

 

6. Compare Gauss-Jacobi and Gauss-Seidel methods.

Solution :

1. Convergence rate is slow

2. Indirect method

3. Condition for convergence is, the coefficient matrix is diagonally dominant

Gauss-Seidel method

1. The rate of convergence of Gauss-Seidel method is fast, roughly twice that of Gauss-Jacobi.

2. Indirect method

3. Condition for convergence is, the coefficient matrix is diagonally dominant.

 

7. Is the iteration method, a self-correcting method always? [M.U. Oct. 1997]

Solution: In general, iteration is a self correcting method, since the round off error is smaller.

 

8. Distinguish between direct and iterative methods of solving simultaneous equations. [A.U Tvli M/J 2011] [A.U A/M 2019 R-17]

Solution:

There are numerical methods of solving simultaneous equations. They are particularly suited for computer operations. These numerical methods are of two types, direct or iterative. Direct methods involve a certain amount of fixed computation and they are exact solutions. Iterative or indirect methods are those in which the solution is got by successive approximations. But the method of iteration is not applicable to all systems of equations.

 

9. When will iteration method succeed?

Solution:

In order that the iteration method may succeed, equation of the system must contain one large coefficient (much larger than the others in that equation) and the large coefficient must be attached to a different unknown in that equation. This requirement will be got when the large coefficients are along the leading diagonal of the matrix of the coefficient.

 

10. Why Gauss-Seidel method is a better method than Jacobi's iterative method ? [A.U A/M 2018 R-13 NM]

Solution:

Since the current values of the unknowns at each stage of iteration are used in proceeding to the next stage of iteration, the convergence in Gauss-Seidel method will be more rapid than in Gauss-Jacobi method.

 

11. Distinguish between direct and iterative (indirect) method of solving simultaneous equations.

Solution :

Direct method

1. We get exact solution

2. Simple, take less time

3. These methods work efficiently upto 100 coefficients.

4. Direct method's performance is affected due to round-off errors.

Iterative method

1. Approximate solution.

2. Time consuming, laborious.

3. These methods can be used for

4. large systems of equations (more than 100)

5. There is no round off error problem.

 

12. Write down the iterative formula of Gauss-Seidal method. [A.U N/D 2014]

Solution:

Consider the system of equations,

 

13. Name the two methods to solve a system of linear simultaneous equations. [A.U M/J 2016]

Solution:

(i) Direct method

(ii) Indirect method (or) Iterative method

 

14. Which of the iterative methods for solving linear system of equations converge faster? Why?  [A.U A/M 2015 R-13] [A.U N/D 2016 R-13]

Solution:

Gauss-Seidel method is solving for linear system of equations converge faster. In this method the rate of convergence is roughly twice as fast as that of Gauss-Jacobi's method.

 

15. What are the various methods of solving simultaneous linear equations? [A.U N/D 2020 (R-17)] [A.U A/M 2021 (R-17)]

Solution :

(1) Direct method

(a) Gauss-Elimination method

(b) Gauss-Jordan method.

(2) Iterative method

(a) Gauss-Jacobi method

(b) Gauss-Seidel method