Significance of Back E.M.F.

Significance of Back E.M.F.

• It is seen in the generating action, that when a conductor cuts the lines of flux, e.m.f. gets induced in the conductor. The question is obvious that in a d.c. motor, after a motoring action, armature starts rotating and armature conductors cut the main flux. So is there a generating action existing in a motor? The answer to this question is 'Yes'.

• After a motoring action, there exists a generating action. There is an induced e.m.f. in the rotating armature conductors according to Faraday's law of electromagnetic induction. This induced e.m.f. in the armature always acts in the opposite direction of the supply voltage. This is according to the Lenz's law which states that the direction of the induced e.m.f. is always so as to oppose the cause producing it. In a d.c. motor, electrical input i.e. the supply voltage is the cause and hence this induced e.m.f.  opposes the supply voltage. This e.m.f. tries to set up a current through the armature which is in the opposite direction to that, which supply voltage is forcing through the conductor.

• So as this e.m.f. always opposes the supply voltage, it is called back e.m.f. and denoted as E_b. Though it is denoted as E_b, basically it gets generated by the generating action which we have seen earlier in case of generators. So its magnitude can be determined by the e.m.f. equation which is derived earlier. So,  E_b = ΦΡΝΖ / 60 A volts

where all symbols carry the same meaning as seen earlier.

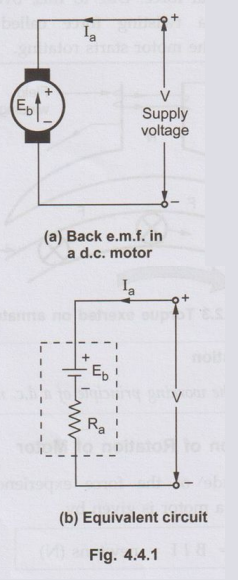
•. This e.m.f. is shown schematically in the Fig. 4.4.1 (a). So if V is supply voltage in volts and R is the value of the armature resistance, the equivalent electric circuit can be shown as in the Fig. 4.4.1 (b).

1. Voltage Equation of a D.C. Motor

• In case of a generator, generated e.m.f. has to supply armature resistance drop and remaining part is available across the load as a terminal voltage. But in case of d.c. motor, supply voltage V has to overcome back e.m.f. E_b, which is opposing V and also various drops as armature resistance drop I_a R_a brush drop etc. Infact the electrical work done in overcoming the back e.m.f. gets converted into the mechanical energy developed in the armature. Hence the voltage equation of a d.c. motor can be written as,

V = E_b + I_a R_a + Brush drop

Neglecting the brush drop, the generalized voltage equation is,

V = E_b+I_aR_a

The back e.m.f. is always less than supply voltage (E_b < V). But R_a is very small hence under normal running conditions, the difference between back e.m.f. and supply voltage is very small. The net voltage across the armature is the difference between the supply voltage and back e.m.f. which decides the armature current. Hence from the voltage equation we can write,

Ia = V-E_b / Ra

Key Point: Voltage equation gets changed a little bit depending upon the type of the motor, which is discussed later.

Ex. 4.4.1 A 220 V, d.c. motor has an armature resistance of 0.75Ω. It is drawing an armature current of 30 A, driving a certain load. Calculate the induced e.m.f. in the motor under this condition.

Sol. : V = 200 V, I_a = 30 A, R_a = 0.75 Ω are the given values

For a motor, V = E_b + I_a R_a

i.e.220 = E_b + 30 x 0.75

Eb = 197.5 volts

This is the induced e.m.f. called back e.m.f. in a motor.

Ex. 4.4.2 A 4 pole, d.c. motor has lap connected armature winding. The flux per pole is 30 mWb. The number of armature conductors is 250. When connected to 230 V d.c. supply it draws an armature current of 40 A. Calculate the back e.m.f. and the speed with which motor is running. Assume armature resistance is 0.6 Ω.

Sol.

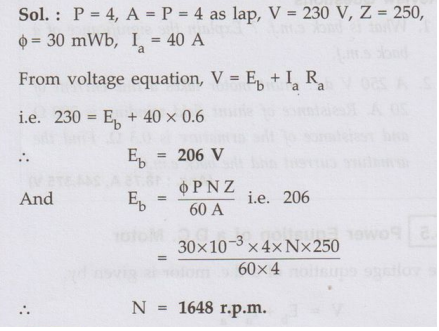
2. Back E.M.F. as a Regulating Mechanism

• Due to the presence of back e.m.f. the d.c. motor becomes a regulating machine i.e. motor adjusts itself to draw the armature current just enough to satisfy the load demand. The basic principle of this fact is that the back e.m.f. is proportional to speed, E_b ∞ N.

•  When load is suddenly put onto the motor, motor tries to slow down. So speed of the motor reduces due to which back e.m.f. also decreases. So the net voltage across the armature (V - E_b) increases and motor draws more armature current. As F = B l I, due to increased current, force experienced by the conductors and hence the torque on the armature increases. The increase in the torque is just sufficient to satisfy increased load demand. The motor speed stops decreasing when the armature current is just enough to produce torque demanded by the new load.

• When load on the motor is decreased, the speed of the motor tries to increase. Hence back e.m.f. increases. This causes (V - E_b) to reduce which eventually reduces the current drawn by the armature. The motor speed stops increasing when the armature current is just enough to produce the less torque required by the new load.

Key Point: So back e.m.f. regulates the flow of armature current and it automatically alters the armature current to meet the load requirement. This is the practical significance of the back e.m.f.

Review Questions

1. What is back e.m.f.? Explain the significance of a back e.m.f.

2. A 250 V d.c. shunt motor takes a line current of 20 A. Resistance of shunt field winding is 200 Ω and resistance of the armature is 0.3 Ω. Find the armature current and the back e.m.f. Ans. 18.75 A, 244.375 V)