Small sample test for difference of means

2. Small sample test for difference of means

t-distribution for difference of means

Suppose, we want to test, if two independent samples x₁, x₂, … n₁ and

y₁, y₂, ... y_n2 of sizes n₁ and n₂ have been drawn from two normal population with means μ₁ and μ₂ respectively.

Under the null hypothesis, H₀ that the samples have been drawn from the normal population with means μ₁ and μ₂ are under the assumption that the population variance are equal. (i.e., σ₁ = σ₂ = σ)

is an unbiased estimate of the population variance σ².

t follows t-distribution with degrees of freedom n₁ + n₂ - 2.

Under the null hypothesis H₀, that (i) samples have been drawn from the population with the same means i.e., µ₁ µ₂, or (ii) the sample means  and  do not differ significantly, take the statistic

If t < table value of t₀ accept0, at a level of significance.

Assumption: The following assumptions are made in using this test.

(i) Parent populations, from which the samples have been drawn are normally distributed.

(ii) Population variances are equal and unknown

(iii) The two samples are random and independent.

S₁, S₂ are standard deviations of the two samples. Therefore, statistic 't' to be tested is

Note 2. If the pairs of values are in some way associated (or correlated), we cannot adopt the case under Note 1. Then, we have to find the differences of the associated pairs of values and apply for single mean

to test, if the means of the differences is significantly different from zero. Then, the degree of freedom is n - 1.

where (x_i, y_i) are the paired data, i = 1,2, … n

Working Procedure :

Concerning difference between two means, with unknown σ²₁ and σ²₂ but equal. (σ₁ = σ₂ = σ). For the small samples (n₁ < 30, n₂ < 30) drawn from two normal population.

1. Null hypothesis H₀: µ₁ = µ₂

2. Alternative hypothesis H₁ : µ₁ ≠ µ₂ (or) µ₁ > µ₂

 (or) µ₁ < µ₂

3. Level of significance: a, d.f. = n₁ + n₂ - 2

4. Critical region :

(a) If µ₁ ≠ µ₂, then the test is two-tailed test for the given ɑ.

The critical values are -ta/2 and ta/2 from the t-distribution table with

d.f. n₁ + n₂ - 2

(b) If µ₁ > µ₂, then the test is one-tailed test (right) for the given ɑ,

The critical value is ta with d.f. n₁ + n₂ - 2

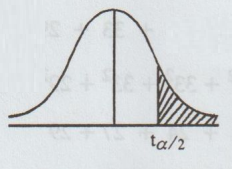
(c) If µ₁ < µ₂, then the test is one-tailed test (left) for the given ɑ,

The critical value is -t_ɑ with d.f.=  n₁ + n₂ - 2

5. The test statistic

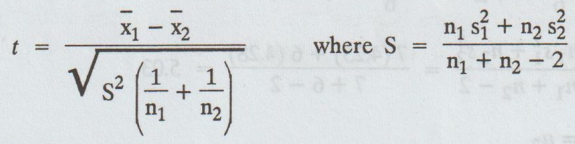
6. Conclusion:

(a) If  - t_ɑ/2 < t < t _ɑ/2, then we accept H₀ for two-tailed test; otherwise, we reject H₀

(b) If t < t_ɑ, then we accept H₀ for one-tailed test (right); otherwise, we reject H₀

(c) If -ta < t_ɑ, then we accept H₀ for one-tailed test (left); otherwise, we reject H₀

 

Example 1.3b(1)

Two horses A and B were tested according to the time (in seconds) to run a particular race with the following results :

6. Conclusion:

Here, Cal t > table t

i.e., 2.5 > 1.796

So, we reject H₀ at 5% level of significance.

 

Example 1.3b(2)

A group of 10 rats fed on diet A and another group of 8 rats fed on diet B, recorded the following increase in weight (gms).

Diet A: 5, 6, 8, 1, 12, 4, 3, 9, 6, 10

Diet B: 2, 3, 6, 8, 10, 1, 2, 8

Does it show superiority of diet A over diet B.

Solution:

Given: n₁ = 10, n₂ = 8

6. Conclusion:

Here, Cal t < table t

i.e. 0.869 < 1.75

So, we accept H_ɑ.

Hence, the difference is not significant, so we cannot conclude that diet A is superior to diet B.

 

Example 1.3b(3)

The following are the number of sales which a sample of 9 sales people of industrial chemicals in Gujarat and a sample of 6 sales people of industrial chemicals in Maharashtra made over a certain fixed period of time:

Assuming that the population sampled can be approximated closely with normal distributions having the same variance, test the null hypothesis μ1 - μ2 = 0 against the alternative hypothesis μ₁ – μ₂ ≠ 0 at the 0.01 level of signifance. [A.U N/D 2009]

Solution: Given: n₁ = 9, n₂ = 6

6. Conclusion:

Here, Cal t < table t

i.e., 1.03 < 3.012

So, we accept H₀ at 1% level of significance.

 

Example 1.3b (4)

The following are the average weekly losses of working hours due to accidents in 10 industrial plants before and after an introduction of a safety program was put into operation.

Use 0.05 level of significance to test whether the safety program is effective.

Solution:

6. Conclusion:

Here, Cal t <  table t

i.e., 0.369 < 2.101

So, we accept Ho at 5% level of significance.

 

Example 1.3b(5)

19diadw test of 93050lingia lo laval 20.0 sa U The following random samples. are measurements of the heat producing capacity (in millions of calories per ton) of specimen's of coals from two mines.

Use the 0.01 level of significance to test whether the difference between the means of these two samples is significant. [A.U. N/D 2008]

Solution :

6. Conclusion:

Here, Cal t > table t

i.e., 4.19 > 3.25

So, we reject H₀

 

Example 1.3b(6) 9ft

Two independent samples are chosen from two schools A and B, a common test is given in a subject. The scores of the students as follows :

Can we conclude that students of school A performed better than students of school B? [A.U. A/M 2008]

Solution :

H₀ : There is no significant difference in the performance of students between school A and school B.

H₁ : The performance of students of school A is better than that of school B.

6. Conclusion:

Here, Cal t < table t

i.e., 0.173 < 1.771

So, we accept Ho at 5% level of significance.

 

Example 1.3.b(7)

In a certain experiment to compare two types of pig foods A and B, the following results of increase in weights were observed in pigs :lol

 (i) Assuming that the two samples of pigs are independent, can we conclude that food B is better than food A ?

(ii) Also, examine the case when the same set of eight pigs were used in both the foods.

Solution: Given n₁ = 8, n₂ = 8

6. Conclusion:

Here, Cal t > table t

i.e., 2.17 > 1.761

So, we reject H₀ at 5% level of significance.

Hence, we conclude that the foods A and B differ significantly as regards their effect on increase in weight, so food B is superior to food A.

(ii) Paired t-test

If the same set of pigs is used in both the cases, then the readings X and Y are not independent but they are paired together and we apply the paired t-test for testing H₀.

6. Conclusion:

Here Cal t > table t

i.e., 4.32 > 1.714

So, we reject H₀ at 5% level of significance.

We conclude that food B is superior to food A.

 

Example 1.3.b(8)

The independent samples from normal populations with equal variance gave the following:

Is the difference between the means significant? [A.U N/D 2019 (R-17)]

Solution :

6. Conclusion :

Here Cal t < table t

i.e., 1.4376 < 2.056

So, we accept H₀ at 5% level of significance.

 

Example 1.3.b(9)

The mean height and the S.D height of 8 randomly chosen soldiers are 166.9 cm and 8.29 cm respectively. The corresponding values of 6 randomly chosen sailors are 170.3 cm and 8.50 cm respectively. Based on this data, can we conclude that solider's are, in general, shorter than sailors? 

Solution :

So, we accept H₀ at 5% level of significance.

i.e., based on the given data, we cannot conclude that soldiers are in general, shorter than sailors.

 

Example 1.3.b(10)

Samples of two types of electric bulbs were tested for length of life and the following data were obtained.

If the difference in the means sufficient to warrant that sample I bulbs are superior to sample II bulbs?

Solution :

6. Conclusion :

Here, Cal t > table t

i.e., 9.39 > 1.771

So, we reject H₀

i.e., sample I bulbs may be regarded superior to sample II bulbs at 5% level of significance.

 

EXERCISES 1.3(b)_

1. Samples of two types of electric light bulbs were tested for length of life and following data were obtained.

Is the difference in the means sufficient to warrant that type I is superior to type II regarding length of life.

Ans. The two types I and II of electric bulbs are not identical

2. The average number of articles produced by 2 machines per day are 200 and 250 with standard deviation 20 and 25 respectively, on the basis of records of 25 days production. Can you regard both the machines equally efficient at 1% level of significance.

Ans. The machine are not equally efficient at 1% level of significant

3. Below are given the gain in weights (in lbs) of pigs fed on two diets A and B.

Test, if the two diets differ significantly, as regards their effect on increase in weight.

Ans. There is no significant difference between the mean increase in weight due to diets A and B.

4. The heights of six randomly chosen sailors are in inches 63, 65, 68, 69, 71 and 72. Those of 10 randomly chosen soldiers are 61, 62, 65, 66, 69, 69, 70, 71, 72 and 73. Discuss the light that these data throw on the suggestion that sailors are on the average taller than soldiers.

Ans. The sailors are not on the average taller than the soldiers. [A.U N/D 2014]

5. Two sets of ten students selected at random from a college were taken: one set was given memory test as they were, and the other was given the memory test; after two weeks of training the scores are given below:

Do you think there is any significant effect due to training? (null and alternative hypothesis should be stated)

Given t = 2.10 at df = 18, ɑ = 0.05)

Ans. There is no significant effect due to training

6. Values of a variate in two samples are given below :

Test the significance of the difference between the two sample means.

Ans. There is no significant difference between the population means.

7. The marks obtained by a group of 9 regular course students and another group of 11 part-time course students in a test are given below :

Examine, whether the marks obtained by regular students and part-time students differ significantly at 5% level of significance and 1% level of significance.

Ans. The marks obtained by regular students and part-time students differ significantly.

8. Two independent samples of size 8 and 7 contained the following values.

Is the difference between the sample means significant?

9. Table gives the biological values of protein from cow's milk and buffalo's milk at a certain level. Examine if the average values of protein in the two samples significantly differ.

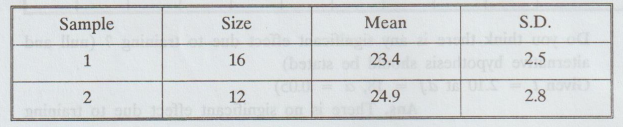
10. Two independent samples from normal populations with equal variance gave the following:

Is the difference between the means significant?

11. A group of five patients treated with medicine A, weight 42, 39, 48, 60, 41 kg; a second group of 7 patients from the same hospital treated with medicine 'B' weigh 38, 42, 56, 64, 68, 69, 62 kg. Do you agree with the claim that medicine B increases the weight significantly?

12. Memory capacity of 9 students was tested before and after a course of meditation for a month. State whether the course was effective or not from the data below (in same units)

13. To compare the prices of a certain product in two cities, ten shops were selected at random in each town. The prices was noted below:

Test whether the average prices can be said to be the same in two cities.