Small Sample Tests

SMALL SAMPLE TESTS

 

1. Small sample test for single mean

I. Student's t

Let x₁, x₂,...x_n be a random sample of size n from a normal population with mean μ and variance σ² .

The student's t test is defined in the statistics as

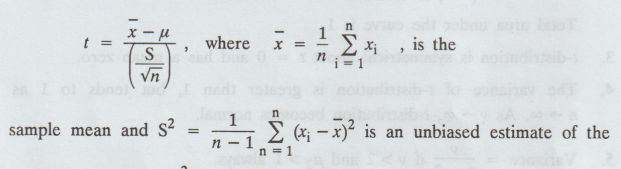
population variance σ² and t follows student's t-distribution with v = n – 1 degrees of freedom with probability density function

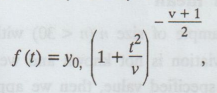
where v = n − 1 and y₀ is a constant determined by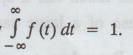 

This is known as 'student's t distribution' or t-distribution

Here, v = n − 1 is called the number of degrees of freedom.

Note: The range of t-distribution is - ∞ to ∞

II. Uses and its applications  [A.U N/D 2011]

1. It is used to test the significance of the difference of the mean of a random sample and the mean of the population

2. It is used to test the significance of the difference between two sample means.

3. To test the significance of an observed sample correlation coefficient and sample regression coefficient.

4. To test the significance of observed partial and multiple correlation coefficients.

III. Properties of t-distribution

1. The variable ranges from - ∞ to ∞

 

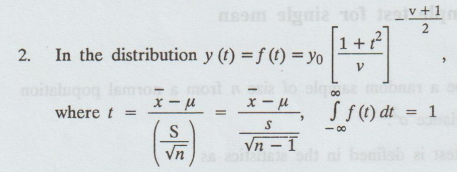
Total area under the curve is 1.

3. t-distribution is symmetrical about t = 0 and has a mean zero.

4. The variance of t-distribution is greater than 1, but tends to 1 as n → ∞. As v → ∞, t - distribution becomes normal.

5. Variance = ν / v – 2 if v > 2 and µ₂ > 1 always.

Test for a specified mean

Given a random sample of size n (n < 30) with sample mean x and the population standard deviation is not known and we want to test whether the population mean has a specified value, then we apply the same procedure as in the case of a large sample.

Working Procedure :

For the small samples (n < 30), σ known, decision is based on the t-distribution with v = n - 1 degrees of freedom. di be bellso a

1. Null hypothesis H₀ : μ = μ₀

2. Alternative hypothesis H₁: μ ≠ μ₀ (or) µ > μ₀ (or) μ < μ₀

3. Level of significance: ɑ

4. Critical region

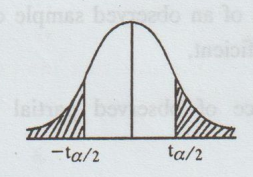
(a) If μ ≠ µ₀, then the test is two-tailed test for the given ɑ.

The critical values are –t_ɑ/2 and ta/2 from the t_ɑ/2 distribution table with d.f. = n - 1

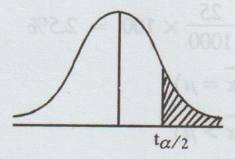
 (b) If µ > µ₀, then the test is one-tail test (right) for the given ɑ

The critical values is t_ɑ with d.f. = n - 1.

(c) If µ < µ₀, then the test is one-tailed test (left) for the given ɑ.

The critical value is -ta with d.f = n - 1.

6. Conclusion :

 (a) If -t _ɑ/2  < t < t _ɑ/2 then we accept H₀; otherwise, add we reject H₀

(b) If t < t_ɑ, then accept H₀, otherwise, we reject H₀

(c) If -ta < t_ɑ then accept H₀, otherwise, we reject H₀.

 

Example 1.3a (1).

Given a sample mean of 83, a sample standard deviation of 12.5 and a sample size of 22, test the hypothesis that the value of the population mean is 70 against the alternative that it is more than 70. Use the 0.025 significance level. [A.U A/M 2018 R-13] 2.5)

Solution :

6. Conclusion :

Here, Cal t > table t

i.e.,  4.77 > 2.08

So, we reject H₀

Mean value of the population is greater than 70.

 

Example 1.3a (2).

A machinist is making engine parts with axle diameters of 0.7 inch. A random sample of 10 parts shows a mean diameter of 0.742 inch with a standard deviation of 0.04 inch. Compute the statistic you would use to test, whether the work is meeting the specification.  [A.U M/J 2006] [A.U A/M 2019 R-13]

Solution:

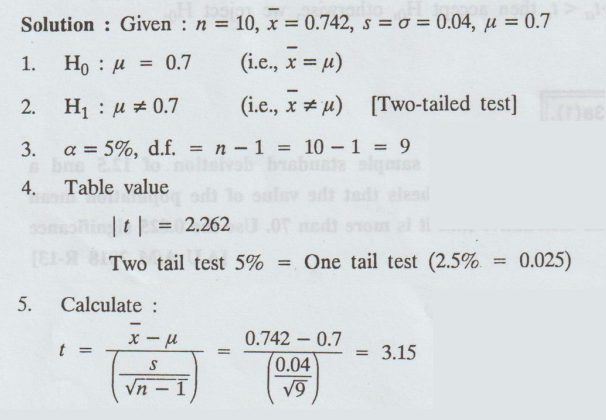
6. Coonclusion :

Here, Cal t > table t

i.e., 3.15 > 2.262

So, we reject H₀

The product is not conforming the specification.

 

Example 1.3a (3)

A certain injection administered to each of 12 patients resulted in the following increases of blood pressure :

5, 2, 8, -1, 3, 0, 6, -2, 1, 5, 0, 4

can it be concluded that the injection will be, in general, accompanied by an increase in B.P?

Solution: Given: n = 12

6. Conclusion :

Here, Cal t > table t

i.e., 2.89 > 1.796

So, we reject H₀

noiaulono

i.e., we may conclude that the injection is accompanied by an increase in B.P.

 

Example 1.3.a(4)

A random sample of 16 values from a normal population showed a mean of 41.5 inches and the sum of squares of deviations from this mean equal to 135 square inches. Show that the assumption of a mean of 43.5 inches for the population is not reasonable. Obtain 95 percent and 99 percent fiducial limits for the same.

Solution:

6. Conclusion:

Here, (i) ɑ = 5%, Cal t >  table t

i.e., 2.75 > 2.131

So, we reject H₀

(ii) ɑ = 1%, Cal t < table t

i.e., 2.75 < 2.941

So, we accept H₀

We conclude that the assumption is reasonable.

7. 95% fiducial limits for µ: (d.f = 15)

 

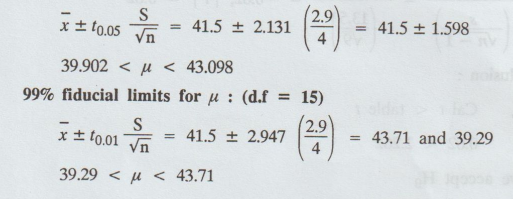
Example 1.3.a(5)

A random sample of 10 boys had the following I.Q's: 70, 120, 110, 101, 88, 83, 95, 98, 107, 100. Do these data support the assumption of a population mean I.Q of 100 ? Find a reasonable range in which most of the mean I.Q. values of samples of 10 boys lie.s

Solution :

[A.U A/M 2015 R-8, N/D 2012 R-8, M/J 2016 R-13] T[A.U N/D 2017 R-13]

Given: n = 10, μ = 100

6. Conclusion:

Here, Cal t < table t

i.e., 0.62 < 2.262

So, we accept H₀

We may conclude that the data are consistent with the assumption of mean I.Q of 100 in the population.

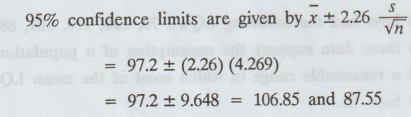
 95% confidence limits within which the mean I.Q values of samples of 10 boys will lie is [87.55, 106.85]

 

Example 1.3a (6)

Sandal Powder is packed into packets by a machine. A random sample of 12 packets is drawn and their weights are found to be (in kg) 0.49, 0.48, 0.47, 0.48, 0.49, 0.50, 0.51, 0.49, 0.48, 0.50, 0.51, and 0.48. Test, if the average weight of the packing can be taken as 0.5 kg. [A.U. N/D 2003]

Solution:

Given: n = 12, μ = 0.5

6. Conclusion:

Here, Cal t > table t

i.e., 2.76 > 2.201

So, we reject H₀

The average packing cannot be taken to be 0.5 kg.

 

Example 1.3a (7)

The mean lifetime of a sample of 25 bulbs is found as 1550 hours with a S.D. of 120 hours. The company manufacturing the bulbs claims that the average life of their bulbs is 1600 hours. Is the claim acceptable at 5% level of significance?

Solution:

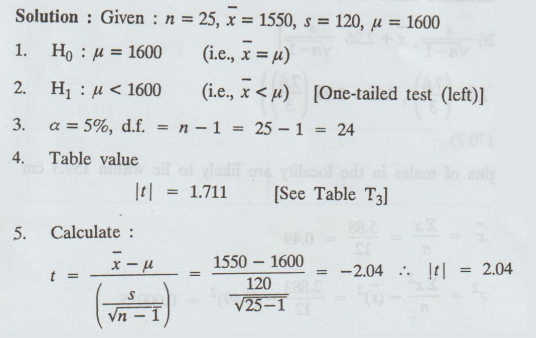
6. Conclusion:

Here Cal t > table t

i.e., 2.04 > 1.711

So, we reject H₀

i.e., The claim of the company cannot be accepted at 5% level of significance.

 

Example 1.3.a (8)

The heights of ten males of a given locality are found to be 175, 168, 155, 170, 152, 170, 175, 160, 160, 165. Based on this sample, find the 95% confidence limits for the height of males in that locality.

Solution: Given: n = 10,

i.e., the heights of males in the locality are likely to lie within 159.3 cm and 170.7 cm

 

Example 1.3.a (9)

A machinist is expected to make engine parts with axle diameter of 1.75cm. A random sample of 10 parts shows a mean diameter 1.85 cm with a s.d. of 0.1 cm. On the basis of this sample, would you say that the work of the [ET olds: 502] aulay oldsT machinist is inferior?

Solution:

 

Example 1.3.a(10)

A test of the breaking strengths of 6 ropes manufactured by a company showed a mean breaking strength of 3515 kg and a standard deviation of 60 kg, whereas the manufacturer claimed a mean breaking strength of 3630 kg. Can we support the manufacturer's claim at a level of significance 0.05. vob bisbrisja [A.U. N/D 2020 (R17), A/M 2020 (R17), A/M 2019 (R17)] @ 10] 1 lo sulsV nonsivabad lo lo so

Solution :

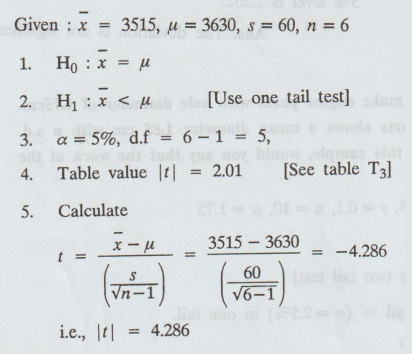
6. Conclusion :

Here Cal t > table t

i.e., 4.286 > 2.01

So, we reject H₀

 

EXERCISE 1.3(a) (Test for a specified mean),

1. Certain refined edible oil is packed in tins holding 16 kg each. The filling machine can maintain this, but with a Standard deviation of 0.5 kg. Samples of 25 are taken from the production line. If a sample mean is (i) 16.35 kg (ii) 15.8 kg, can we be 95% sure that the sample has come from a population of 16 kg tins ?

Ans. The population mean can be equal to 16 kg.

2. A random sample of 9 items is taken from a certain measurement. From the data, it is found that Σ X = 108, Σ X² = 1584. Find the confidence limits for the population mean at 5% level of significance and test the alue of t at 5% level hypothesis that the population mean is 8. Table value of t at 5% level for 8 d.f and 9 d.f are respectively 2.306 and 2.226.

Ans. The population mean is 8 is valid.

3. A machine is designed to produce insulating washers for electrical devices of average thickness of 0.025 cm. A random sample of 10 washers was found to have an average thickness of 0.024 cm with a standard deviation of 0.002 cm. Test the significance of the deviation. Value of t for 9 degrees of freedom at 5% level is 2.262.

Ans. The deviation is not significant.

4. A company has been producing steel tubes of mean inner diameter of 2.00 cm. A sample of 10 tubes gives an inner diameter of 2.01 cm and a variance of 0.004 cm2. Is the difference in the value of mean significant ?

Value of t for 9 d.f at 5% level = 2.262.

Ans. The means of the population and the sample are not significant.

5. A filling machine is expected to fill 5 kg of powder into bags. A sample of 10 bags gave the weights 4.7, 4.9, 5.0, 5.1, 5.4, 5.2, 4.6, 5.1, 4.6 and 14.7. Test

Ans. The machine is working properly.

6. Eight individuals are chosen at random from a population and then, heights are found to be in cms. 163, 163, 164, 165, 166, 169, 170, 171. In the light of these data, discuss the suggestion that the mean height diw in the universe in 165 cms.

Ans. The mean height can be regarded as 165 cms.

7. Ten students are selected at random from a college and then heights are found to be 100, 104, 106, 110, 118, 120, 122, 124, 126 and 128 cms. In the light of these data, discuss the suggestio.. that the mean height of the students of the college is 110 cm. The table value of t at 5% level for 8 d.f is 2.306 and for 9 d.f is 2.262 and 10 d.f is 2.228 for a two-tail test.

Ans. The mean height of the population can be regarded as 110 cms.

8. A fertilizer mixing machine is set to give 12 kg of nitrate for every quintal bag of fertilizer. Ten 100 kg bags are examined and percentage of nitrate is as follows :

11, 14, 13, 12, 13, 12, 13, 14, 11, 12

Is there reason to believe that the machine is defective?

Ans. The machine is not defective

9. The heights of 10 males of a given locality are found to be 175, 168, 155, 170, 152, 170, 175, 160, 160 and 165 cms. Based on this sample of 10 items, test the hypothesis that the mean height of males is 170 cms. 

Ans. The mean height of males can be regarded as 170 cms.

10. The mean weekly sales of a powder in supermarket was 146.3 tins. After a special advertising campaign the mean weekly sales in 22 branches in a week increased to 153.7 tins and showed a S.D. 17.2 tins. Was the advertising campaign successful?

11. The nine items of a sample have the following values: 45, 47, 50, 52, 48, 47, 49, 53, 51. Does the mean of these values differ significantly from the assumed mean 47.5? [for v = 8, t0.05 = 2.31]

12. A spare parts manufacturer is making spare parts with axle diameter of 0.700 inch. A random sample of 10 parts shown a mean diameter of 0.742 inch with a S.D of 0.040 inch. Verify whether the work satisfies the specifications.

13. A sample of 20 items has mean 42 units and S.D 5 units. Test the hypothesis that it is a random sample from a normal population with mean 45 units.

14. The following results are obtained from a sample of 10 boxes of biscuits.

Mean weight content =  490 gm

S.D. of weight = 9 gm

rigio Could the sample come from a population having a mean of 500 gm?

15. The average breaking strength of steel rods is specified, to be 17.5 (in units of 1000 kg). To test this, sample of 14 rods tested and gave the following results: 15, 18, 16, 21, 19, 21, 17, 17, 15, 17, 20, 19, 17, 18. Is the result of the experiment significant? Also obtain 95% confidence Istni A interval for the average breaking strength?