Solution of Equations and Eigenvalue Problems

UNIT - III

SOLUTION OF EQUATIONS AND EIGENVALUE PROBLEMS

SOLUTION OF ALGEBRAIC AND TRANSCENDENTAL EQUATIONS

Analytical methods of solving cubic and quadratic equations are available. Polynomial equations of degree greater than 4 are not solvable in analytical form and have to be solved by numerical methods to reach at a solution as correct as possible to the desired accuracy.

On many occasions, we come across transcendental equation in engineering. Analytical methods do not exist for solving such equations. We have to use only numerical techniques to solve them. In this chapter, we shall discuss numerical methods for the solution of algebraic and transcendental equations.

Algebraic equation :

An expression is of the form

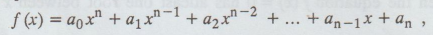
where a₀, a₁, ..., a_n are constants (ao 0) and n is a positive integer, is called a polynomial in x of degree n. The polynomial f (x) = 0 is called an algebraic equation of degree n.

Example: 5x⁷ + 3x² +7x + 8 = 0, 2x³ -3x - 6 = 0

Note 1: An equation f (x) = 0 is said to be algebraic, if f (x) is purely a polynomial in x.

Transcendental equation :

Equations which are not purely algebraic are called transcendental equations, i.e., if f (x) contains some other functions such as trigonometric, logarithmic, exponential etc, then f(x) = 0 is called a transcendental equation.

Example : 2x + e^x – 5 = 0, x + cos x + 2 = 0, log₁₀ x – 5 = 0

Note 2: Every algebraic equation has atleast one root and an n^th degree equation has exactly n roots, real, imaginary and complex.

Note 3 : A transcendental equation may have no root or any number of roots.

The roots of this equation may be real or imaginary.

Roots of an equation :

If f (x) = 0 be an equation and a be a value of x such that ƒ (a) = 0, then a is a root of the equation f (x) = 0

Methods of finding accurate roots :

The following computer oriented methods are used to find an accurate real root of the equation f (x) = 0.

1. Bolzano's method of bisection

2. Method of regula falsi

3. Secant method

4. Method of direct iteration (method of fixed point)

5. Newton-Raphson method (method of tangent)

Basic properties of equations :

1. If a polynomial of degree n vanishes for more than n values of x, then it must be identically zero.

2. Every equation of odd degree has atleast one real root.

3. If f (x) is continuous in the interval [a, b] and f (a), f (b) have different signs, then the equation f (x) = 0 has atleast one root between x = a and x = b

4. Descarte's rule of signs.

1. An equation f (x) = 0 cannot have more number of positive roots than there are changes of sign in the terms of the polynomial f (x).

2.  An equation f (x) = 0 cannot have more number of negative roots than there are changes of sign in the terms of the polynomial f (-x).