Electric Circuit Analysis: Unit I: b. Basic circuits analysis
Some important terms
Wave form, Cycle, Time period, Frequency, Amplitude | Basic circuits analysis
Wave form : It is the graph drawn between the alternating quantity (only instantaneous value) as ordinate and time as abscissa.
SOME IMPORTANT TERMS
(i) Wave form
It
is the graph drawn between the alternating quantity (only instantaneous value)
as ordinate and time as abscissa.
The
alternating quantity may be either voltage or current or flux. Accordingly, the
wave form is known as voltage wave form, current wave form or flux wave form.
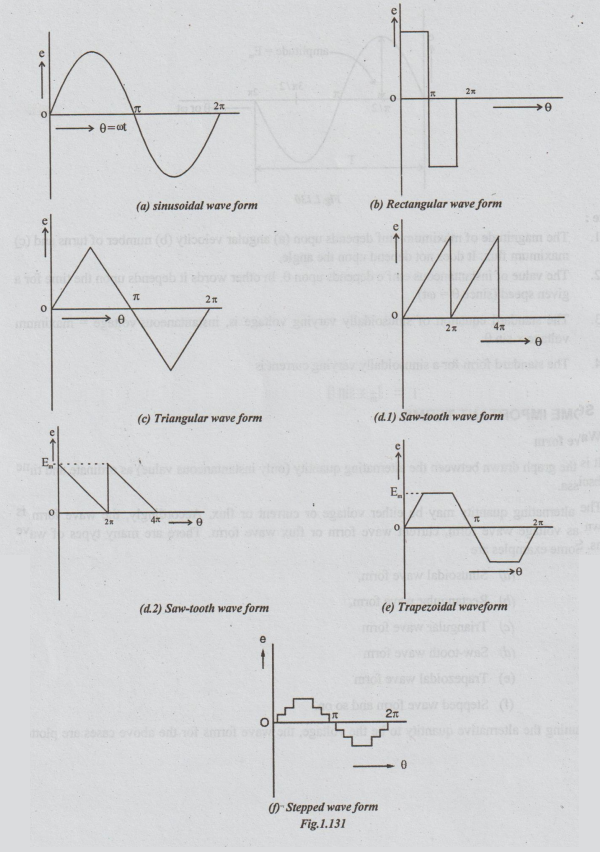
There are many types of wave forms. Some examples are
(a)
Sinusoidal wave form,
(b)
Rectangular wave form,
(c)
Triangular wave form
(d)
Saw-tooth wave form
(e)
Trapezoidal wave form
(f)
Stepped wave form and so on.
Assuming
the alternative quantity to be the voltage, the wave forms for the above cases
are plotted below.
Note:
1.
Only few types of wave forms are shown above.
2.
The reader must be able to draw the wave form when its equation is given.
3.
He or she must also be able to write the equation when the wave form is given.
4.
Our discussion is confined only to sinusoidal wave form. The definition for
various other terms are confined to sinusoidal wave form.
(ii) Cycle
It
is a set of positive and negative portions of wave form
(iii) Time period
The
time required for an alternating quantity to complete one cycle is called the
time period and is denoted by T.
(iv) Frequency
The
number of cycles per second is called frequency and is denoted by f. It is
measured in cycles/second (cps) or Hertz (Hz).
From
definitions of T and f, we can write that
f
= 1 / T
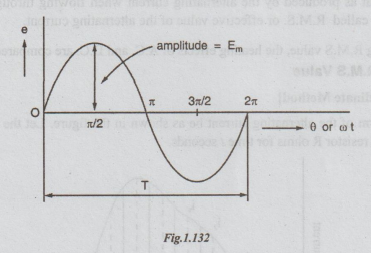
(v) Amplitude
The
maximum value of the alternating quantity in a cycle, is called amplitude. It
is also known as peak value or crest value. In the voltage wave form shown in
Fig (1.75), the peak value is Em. It is obtained when the angle is π/2 (positive cycle) and 3π/2 (negative cycle).
Relation
between ω and f
Angular
distance = angular velocity × time
i.e.,
θ = ω × t ... (4)
When
θ = 360° = 2π radians, one cycle is completed.
Then
time t = time taken for completion of one cycle = T. Substituting these values
in equation (4) we get
2π
= ωT
⇒ ω 2π / T
⇒ ω 2πf
Electric Circuit Analysis: Unit I: b. Basic circuits analysis : Tag: : Wave form, Cycle, Time period, Frequency, Amplitude | Basic circuits analysis - Some important terms
Electric Circuit Analysis: Unit I: b. Basic circuits analysis
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation