Speed Control of D.C. Shunt Motor

Speed Control of D.C. Shunt Motor

AU: Nov.-04, Oct.-98, April-97, Dec.-05,06,07,08,14,17,18

May-05,06,07,08,10,11,12,13,14,17,19

• Out of the three methods, let us study flux control method.

 

1. Flux Control

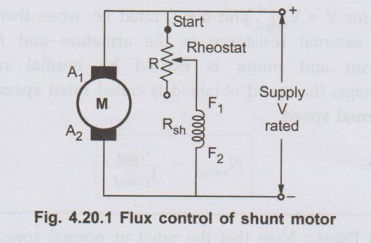
• As indicated by the speed equation, the speed is inversely proportional to the flux. The flux is dependent on the current through the shunt field winding. Thus flux can be controlled by adding a rheostat (variable resistance) in series with the shunt field winding, as shown in the Fig. 4.20.1.

• At the beginning the rheostat R is kept at minimum indicated as start in the Fig. 4.20.1. The supply voltage is at its rated value. So current through shunt field winding is also at its rated value. Hence the speed is also rated speed also called normal speed. Then the resistance R is increased due to which shunt field current I_sh decreases, decreasing the flux produced. As N ∝ 1 / ϕ), the speed of the motor increases beyond its rated value.

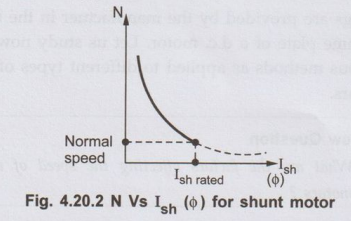
• Thus by this method, the speed control above rated value is possible. This is shown in the Fig. 4.20.2, by speed against field current curve. The curve shows the inverse relation between N and o as its nature is rectangular hyperbola.

• It is mentioned that the rated values of electrical parameters should not be exceeded but the speed which is mechanical parameter can be increased upto twice its rated value.

a. Advantages of Flux Control Method

1. It provides relatively smooth and easy control.

2. Speed control above rated speed is possible.

3. As the field winding resistance is high, the field current is small. Hence power loss (I²_sh R) in the external resistance is very small, which makes the method more economical and efficient.

4. As the field current is small, the size of the rheostat required is small.

b. Disadvantages of Flux Control Method

1. The speed control below normal rated speed is not possible as flux can be increased only upto its rated value.

2. As flux reduces, speed increases. But high speed affects the commutation making motor operation unstable. So there is limit to the maximum speed above normal, possible by this method.

 

2. Armature Voltage Control Method or Rheostatic Control

• The speed is directly proportional to the voltage applied across the armature. As the supply voltage is normally constant, the voltage across the armature can be controlled by adding a variable resistance in series with the armature as shown in the Fig. 4.20.3.

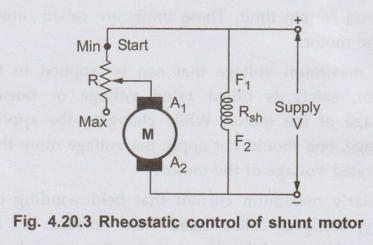
• The field winding is excited by the normal voltage hence Ish is rated and constant in this method. Initially the rheostat position is minimum and rated voltage gets applied across the armature. So speed is also rated. For a given load, armature current is fixed. So when extra resistance is added in the armature circuit, I_a remains same and there is voltage drop across the resistance added (I_aR_a). Hence voltage across the armature decreases, decreasing the speed below normal value. By varying this extra resistance, various speeds below rated value can be obtained.

• So for a constant load torque, the speed is directly proportional to the voltage across the armature. The relationship between speed and voltage across the armature is shown in the Fig. 4.20.4.

a. Potential Divider Control

• The main disadvantage of the above method is, the speed upto zero is not possible as it requires a large rheostat in series with the armature which ispractically impossible. If speed control from zero to the rated speed is required, by rheostatic method then voltage across the armature can be varied by connecting rheostat in a potential divider arrangement as shown in the Fig. 4.20.5.

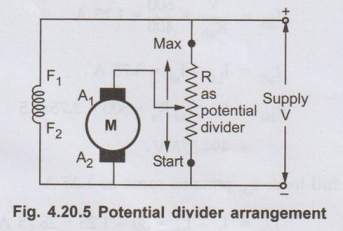
• When the variable rheostat position is at 'start' point shown, voltage across the armature is zero and hence speed is zero. As rheostat is moved towards 'maximum' point shown, the voltage across the armature increases, increasing the speed. At maximum point the voltage is maximum i.e. rated hence maximum speed possible is rated speed. The relationship is shown in the Fig. 4.20.6.

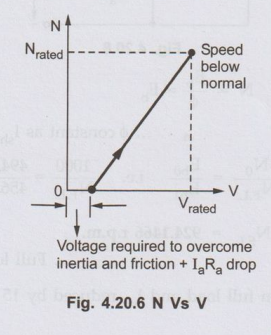
•  When the voltage across the armature starts increasing, as long as motor does not overcome inertial and frictional torque, the speed of the motor remains zero. The motor requires some voltage to start hence the graph of voltage and the speed does not pass through the origin as shown in the Fig. 4.20.6.

b. Advantages of Rheostatic Control

1. Easy and smooth speed control below normal is possible.

2. In potential divider arrangement, rheostat can be used as a starter.

c. Disadvantages of Rheostatic Control

1. As the entire armature current passes through the external resistance, there are tremendous power losses.

2. As armature current is more than field current, rheostat required is of large size and capacity.

3. Speed above rated is not possible by this method.

4. Due to large power losses, the method is expensive, wasteful and less efficient.

5. The method needs expensive heat dissipation arrangements.

 

3. Applied Voltage Control

• Multiple voltage control: In this technique the shunt field of the motor is permanently connected to a fixed voltage supply, while the armature is supplied with various voltages by means of suitable switch gear arrangements.

• The Fig. 4.20.7 shows a control of motor by two different working voltages which can be applied to it with the help of switch gear. 

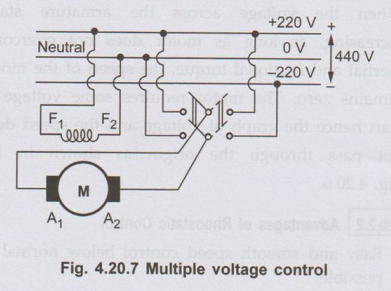
• In large factories, various values of armature voltages and corresponding arrangement can be used to obtain the speed control.

a. Advantages of Applied Voltage Control

1. Gives wide range of speed control.

2. Speed control in both directions can be achieved very easily.

3. Uniform acceleration can be obtained.

2. Disadvantages of Applied Voltage Control

1. Arrangement is expensive as provision of various auxiliary equipments is necessary.

2. Overall efficiency is low.

* General steps to solve problems on speed control

 1. Identify the method of speed control i.e. in which winding of the motor, the external resistance is to be inserted.

2.Use the torque equation, T ∝ ϕ I_a to determine the new armature current according to the condition of the torque given. Load condition indicates the condition of the torque.

3. Use the speed equation N ∞ E_b  / Φ to find the unknown back e.m.f. or field current.

4. From the term calculated above and using voltage current relationship of the motor, the value of extra resistance to be added, can be determined. The above steps may vary little bit according to the nature of the problem but are always the base of any speed control problem.

Ex. 4.20.1 A 500 V d.c. shunt motor has armature and field resistances of 1.5 Ω and 400 Ω respectively. When running on no load the current taken is 5 Amps and the speed is 1000 r.p.m. Calculate the speed when motor is fully loaded and the total current drawn from the supply is 30 Amps. Also estimate the speed at this load if the shunt field current is reduced by 15 %.

AU: Nov.-04, Marks 8

Sol.

Ex. 4.20.2 A 15 kW, 250 V, 1200 r.p.m. shunt motor has 4 poles, 4 parallel armature paths and 900 armature conductors. Assume R_a = 0.2 •Ω. At rated speed and rated output the armature current is 75 A and I_f = 1.5 A Calculate i) The flux/pole ii) The torque developed iii) Rotational losses iv) Efficiency v) The shaft load vi) If the shaft load remains fixed, but the field flux is reduced to 70% of its value by field control, determine the new operating speed.

AU: Dec.-05, Marks 10

Sol. :

Ex 4.20.3 A 500 V d.c. shunt motor running at 700 r.p.m. takes an armature current of 50 A and effective armature resistance is 0.4 Ω. What resistance must be placed in series with the armature to reduced the speed to 600 r.p.m., the torque remaining constant.

AU: May-06, Marks 8

Sol. :

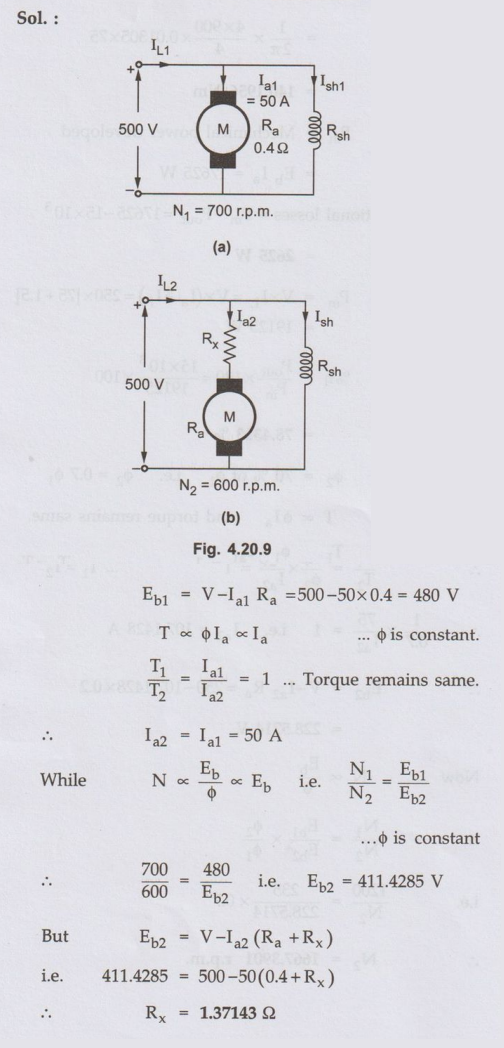
Ex. 4.20.4 A 230 V DC shunt motor has an armature circuit resistance of 0.4 Ω and field resistance of 115 Ω. The motor drives a constant torque load and takes an armature current of 20 A at 800 rpm. If motor speed is to be raised from 800 to 1000 rpm, find the resistance that must be inserted in the shunt filed circuit.

AU: May-07, Dec.-18, Marks 13

Sol. :

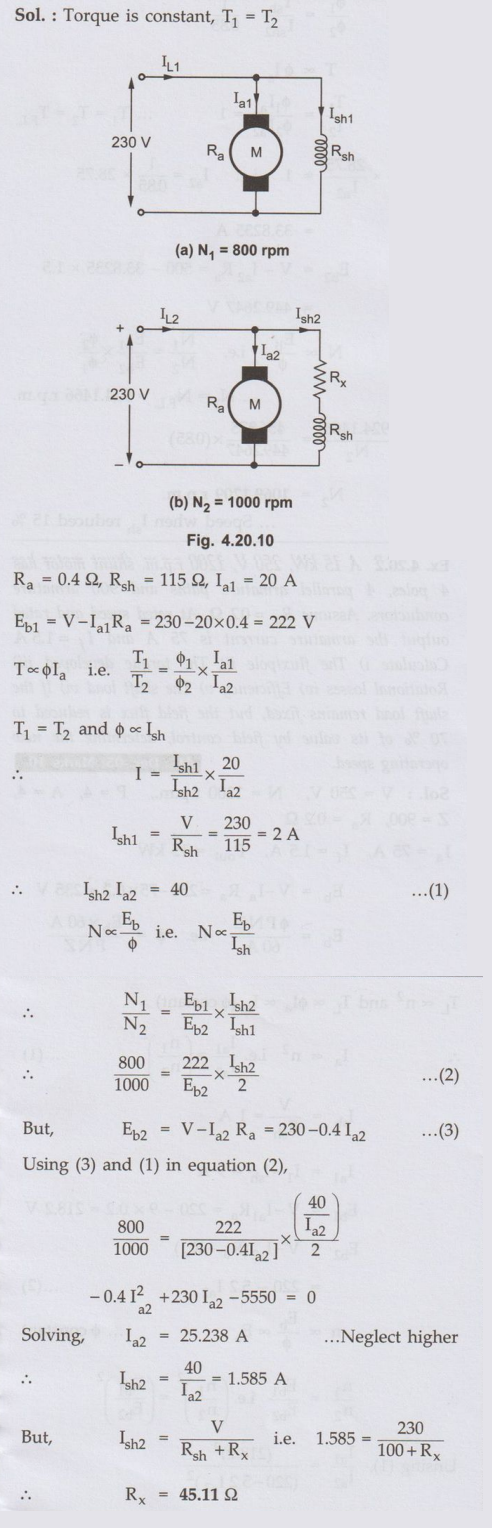
Ex. 4.20.5 A 250-V dc shunt motor has R_f = 150 Ω and R_a = 0.6 Ω. The motor operates on no-load with a full field flux at its base speed of 1000 r.p.m. with I_a = 5 A. If the machine drives a load requiring a torque of 100 Nm, calculate armature current and speed of motor. If the motor is requird to develope 12 kW at 1200 r.p.m. what is the required value of the external series resistance in the field circuit? Assume linear magnetization. Neglect saturation and armature reaction. AU: Dec.-07, May-11, Marks 16

Sol.:

Ex. 4.20.6 A 220V shunt motor has armature and field resistances of 0.2 Ω and 220Ω respectively. The motor is driving load torque T_L ∝n² and running at 1000 rpm drawing 10 A current from the supply. Calculate the new speed and armature current of an external armature resistance of value 52 is inserted in the armature circuit. Neglect armature reaction and saturation.

AU:May-19, Mark 13

Sol. :

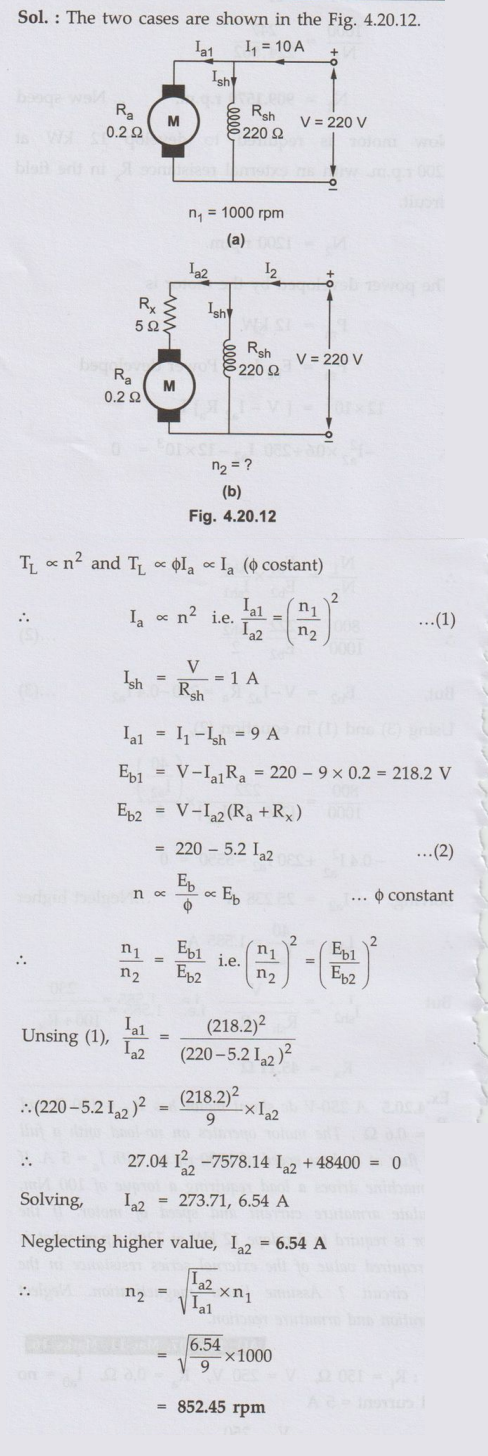
Review Questions

1. Explain the methods of speed control of d.c. shunt motor with the help of neat diagrams.

AU: May-05 08,10,12,13,17, Dec.-05,06,08,14,17, Marks 8

2. Discuss in detail about shunt armature speed control of d.c. shunt motor.

AU: May-06,14, Dec.-07, Marks 8

3. A 250 V d.c. shunt motor has a shunt field resistance of 200 Ω and an armature resistance of 0.3Ω. For a given load, motor runs at 1500 r.p.m. drawing a current of 22 A from the supply. If a resistance of 150 Ω is added in series with the field winding, find the new armature current and the speed. Assume load torque constant and magnetization curve to be linear.

(Ans.: 36.3125 A, 2575.03 r.p.m.)

4. A 250 V, 10 h.p., d.c. shunt motor with R_a = 0.4 Ω and R_sh = 100 Ω, runs at 1000 r.p.m. on full load. Efficiency on full load is 85 %. If speed is to be raised to 1400 r.p.m. keeping load constant, determine extra resistance to be added in the field circuit. Assume 1 h.p = 735.5 watts. 

(Ans. : 43.362)

 5. A 220 V d.c. shunt motor has an armature resistance of 0.5 Ω and is excited to produce constant flux. At full load the motor runs at no1000 r.p.m. taking an armature current of 40 A. If a resistance of 0.8 Ω is inserted in series with the armature, determine speed at the full load.

AU: April-97 (Ans.: 840 r.p.m.)

6. A 230 V d.c. shunt motor runs at 1000 r.p.m. on full load, drawing a current of 10 A. The shunt field resistance is 230 Ω and the armature resistance is 0.5 Ω. Calculate the resistance to be inserted in series with the armature so that the speed at full load is 950 r.p.m. AU: Oct.-98

(Ans.: : 1.25282)

7. A 250 V d.c. shunt motor has R_f = 150 Ω R_a = 0.6 9. The motor operates on no load r.p.m. with a full field flux at its base speed of 1000 r.p.m. with I_a= 5 A. If the machine drives a load requiring a torque of 100 Nm, calculate armature current and speed of motor. If the motor is required to develop 10 kW at 1200 r.p.m., what is the required value of the external series resistance in the field circuit?

AU: Dec.-07 

(Ans.: 42.3966 A, 909.1579 r.p.m.,55.052 Ω)