Spherical Capacitor

Spherical Capacitor

AU ; Dec.-03, 06, May-04, 06, 09, 19

• Consider a spherical capacitor formed of two concentric spherical conducting shells of radius a and b. The capacitor is shown in the Fig. 5.15.1.

• The radius of outer sphere is 'b' while that of inner sphere is 'a'. Thus b > a. The region between the two spheres is filled with a dielectric of permittivity e. The inner sphere is given a positive charge + Q while for the outer sphere it is - Q.

• Considering Gaussian surface as a sphere of radius r, it can be obtained that  is in radial direction and given by,

• The potential difference is work done in moving unit positive charge against the direction of E i.e. from r = b to r = a.

1. Capacitance of Single Isolated Sphere

• Consider a single isolated sphere of radius 'a', given a charge + Q. It forms a capacitance with an outer plate which is infinitely large hence b = ∞

• The capacitance of such a single isolated spherical conductor can be obtained by substituting b = in the equation (5.15.4).

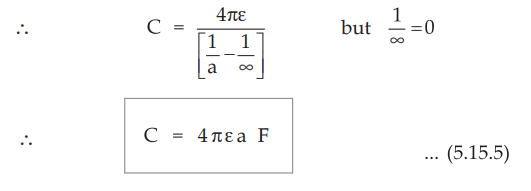
• This is the case of a spherical conductor at a large distance from other conductors. Practically this fact is important in obtaining the stray capacitance of an isolated body.

2. Isolated Sphere Coated with Dielectric

• Consider a single isolated sphere coated with a dielectric having permittivity Ɛ₁ upto radius r₁. The radius of inner sphere is 'a' as shown in the Fig. 5.15.2. It is placed in a free space so outside sphere e = e 0. It carries a charge + Q.

• The potential difference is work done in bringing unit positive charge from outer sphere r = to inner sphere r = a against . This is to be splitted in two as,

• Thus total capacitance can be treated to be the two capacitors C₁ and C₂ in series.

Ex. 5.15.1 Find the capacitance of a conducting sphere of 2 cm in diameter, covered with a layer of polyethelene with Ɛr = 2.26 and 3 cm thick.

AU : May-06,19, Marks 15

Sol. : The sphere is shown in the Fig. 5.15.3.

But between this sphere of radius r1 and sphere at ∞ the dielectric is free space Ɛ0.

Ex. 5.15.2 A spherical condenser has a capacity of 54 pF. It consists of two concentric spheres differing in radii by 4 cm and having air as dielectric. Find their radii.

Sol. : C = 54 pF and b - a = 4 cm, Ɛr = 1

The spherical capacitor has a capacitance,

Ex. 5.15.3 Evaluate the capacitance of

AU : May-04, Marks 16

i) A spherical satellite 1.5 m diameter in free space.

ii) A co-axial cable 1.5 m long filled with polyethylene (er = 2.26) with inner conductor of radius 0.6 mm and inner radius of outer conductor 3.5         mm.

iii) An infinitely long conductor with 1.5 mm radius and suspended horizontally at a height of 15 m above a conducting plane and parallel to it in air.

Sol. :

i) The capacitance of a single isolated sphere is,

iii) Consider the cylindrical conductor suspended above the conducting plane as shown in the Fig. 5.15.4

Examples for Practice

Ex. 5.15.4 Find the capacitance of a conducting sphere of 2 cm in diameter, covered with a layer of polyethelene with Ɛ_r = 2.26 and 3 cm thick.

[Ans.: 1.9121 pF]

Ex. 5.15.5 A spherical capacitor consists of two thin metallic spheres of radii 1 cm and 2 cm. If it is filled with an insulator having dielectric constant 2, find it’s capacitance.

[Ans.: 4.4505 pF]

Review Questions

1. Derive the expression for capacitance of spherical capacitor.

2. Derive the expression for capacitance of isolated sphere.

3. Derive the expression for capacitance of isolated sphere coated with dielectric.