Stress-strain diagram

STRESS-STRAIN DIAGRAM:

Ductile Materials: Materials like Mild Steel, Copper, etc., can be drawn into thin wires. These are therefore called as Ductile Materials.

Brittle Materials: Brittle Materials do not deform on loading. They break suddenly at the time of failure. Examples: Cast Iron, Glass, etc.

Elasticity: When a body is subjected to a force or load, it undergoes deformation. On the removal of load, if it regains its original shape and size (i.e., all the deformation vanishes), then the body is said to behave in a perfectly elastic manner.

Elasticity is the property of a material to regain its original shape and size completely on the removal of external load acting on it. Example: Mild Steel

Plasticity: Plasticity is the property of a material which does not come back to its original shape and size on the removal of external load acting on it. Example: Lead.

1. TENSION TEST FOR MILD STEEL

See Fig. 7. It shows the stress-strain relationship of the Tension Test conducted on a specimen bar of uniform cross-section of ductile metal Mild Steel. The various stages passed through by the specimen before it breaks are explained as follows:

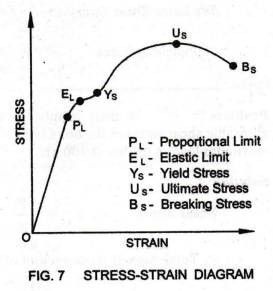
Proportional Limit or Limit of Proportionality (PL): See Fig. 7. From the origin O to a point PL, the stress-strain diagram is a straight line. In the range O to P_L, the stress is proportional to the strain.

Also, the specimen will regain its original shape and size after unloading. The stress corresponding to the load at P_L is known as Proportional Limit or Limit of Proportionality.

Elastic Limit (E_L): See Fig. 7. Beyond P_L, the stress is not proportional to the strain. It means that the proportionality between stress and strain ends at the limit of proportionality. Thus, the material ceases to obey Hooke's Law beyond the limit of proportionality.

Point El represents the Elastic Limit. This is the limit up to which the strain produced will disappear completely on the removal of load. The stress corresponding to the load at Eų is known as Elastic Limit. Any loading beyond E_L will cause permanent deformation. It is called Permanent Set in the material.

Yield Stress (Ys): See Fig. 7. Loading beyond El causes elongation much larger than the elongations observed earlier. At the point Ys, the material yields to a great extent. The stress corresponding to the load is known as Yield Stress Ys.

Yield Stress = Ys = Yield Load / Original Area of Cross-section (A)

Ultimate Stress (Us): The maximum stress that a material can withstand before its failure is known as Ultimate Stress Us.

Ultimate Stress = Us = Maximum Load or Ultimater Load / Original Area of Cross-section (A)

In this stage, a part of the length reduces in its diameter. In that part, a neck or waist is started forming. Now, the specimen goes rapidly to rupture. The nominal stress at which the rupture occurs is called Rupture Strength.

Nominal Stress at Rupture = Load at Rupture / Original Area of Cross-section (A)

Actual Stress at Rupture = Load at Rupture / Neck Area of Cross-section

Breaking Stress (Bs): The stress corresponding to the load at which the material fails or breaks is known as Breaking Stress Bs.

The nominal stress at breaking calculated based on the original area of cross section of the specimen will be less than the nominal ultimate stress. However, the actual stress at breaking calculated based on the actual (neck) cross sectional area of the specimen at the time of breaking will be greater than the ultimate stress.

Nominal Stress at Breaking = Load at Breaking /  Original Area of Cross-section (A)

Actual Stress at Breaking = Load at Breaking / Neck Area of Cross-section