Subtractors

Subtractors

• The subtraction consists of four possible elementary operations, namely,

AU: Dec.-14, 15, 16

0 - 0 = 0

0 - 1 = 1 with 1 borrow

1 - 0 = 1

1 - 1 = 0

• In all operations, each subtrahend bit is subtracted from the minuend bit. In case of second operation the minuend bit is smaller than the subtrahend bit, hence 1 is borrowed. Just as there are half and full-adders, there are half and full-subtractors.

1. Half Subtractor

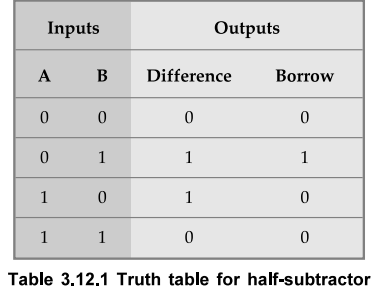
• A half-subtractor is a combinational circuit that subtracts two-bits and produces their difference. It also has an output to specify if a 1 has been borrowed. Let us designate minuend bit as A and the subtrahend bit as B. The result of operation A - B for all possible values of A and B is tabulated in Table 3.12.1.

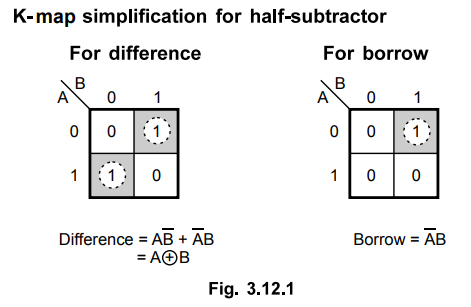
• As shown in the Table 3.12.1, half-subtractor has two input variables and two output variables. The Boolean expression for the outputs of half-subtractor can be determined as follows.

Limitations of half-subtractor :

• In multidigit subtraction, we have to subtract two bits along with the borrow of the previous digit subtraction. Effectively such subtraction requires subtraction of three bits. This is not possible with half-subtractor.

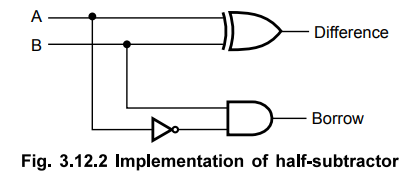
Logic diagram

Ex. 3.12.1 Draw half subtractor using NAND gates.

Sol. : For half subtractor :

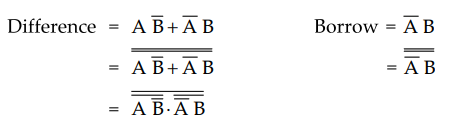
Implementation :

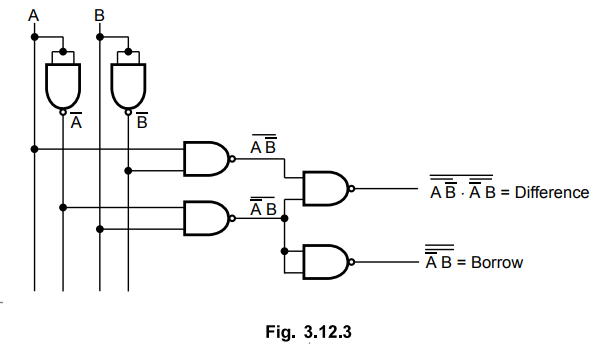
2. Full-Subtractor

A full-subtractor is a combinational circuit that performs a subtraction between two bits, taking into account borrow of the lower significant stage. This circuit has three inputs and two outputs. The three inputs are A, B and B^, denote the minuend, subtrahend and previous borrow, respectively. The two outputs, D and B represent the difference and output borrow, respectively. The Table 3.12.2 shows the truth table for full-subtractor.

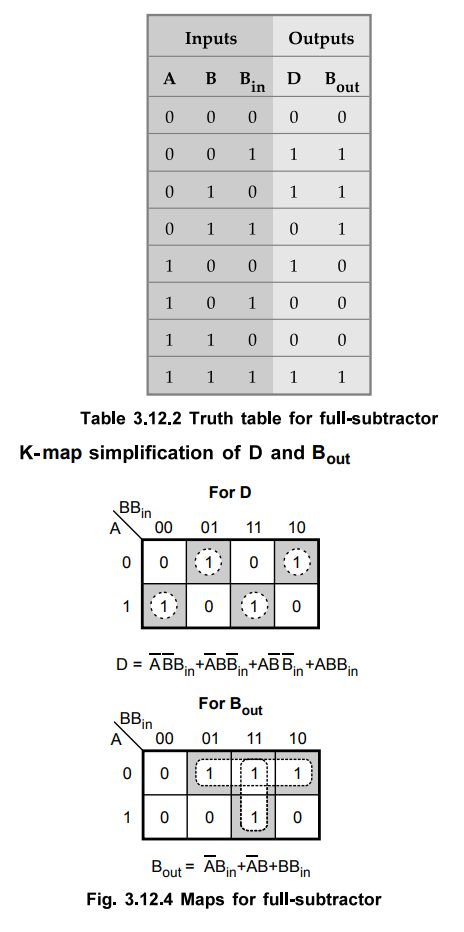
Logic diagram

• The Boolean function for D (difference) can be further simplified as follows :

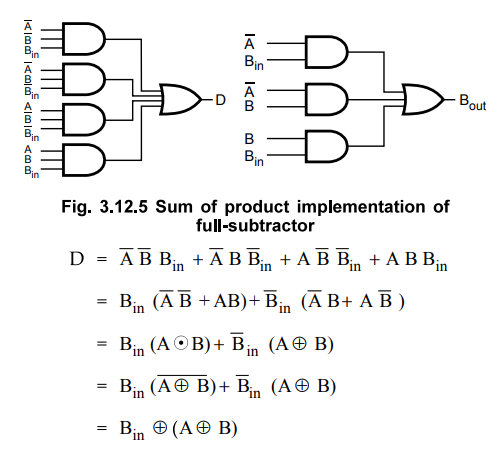
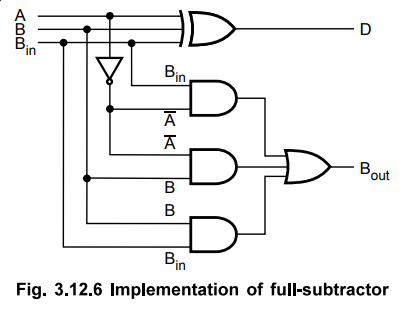
• With this simplified Boolean function circuit for full-subtractor can be implemented as shown in the Fig. 3.12.6

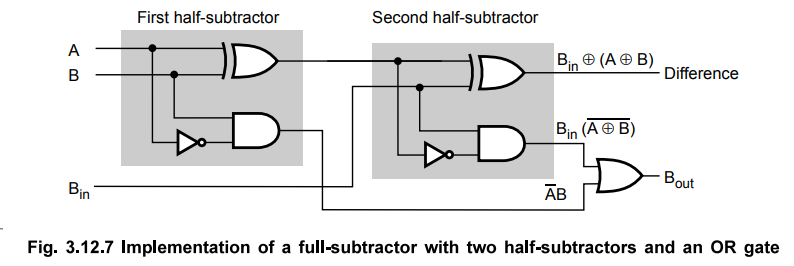
• A full subtractor can also be implemented with two half-subtractors and one OR gate, as shown in the Fig. 3.12.7. The difference output from the second half-subtractor is the exclusive-OR of B. and the in output of the first half-subtractor, which is same as difference output of full-subtractor.

• The borrow output for circuit shown in Fig. 3.12.6 can be given as,

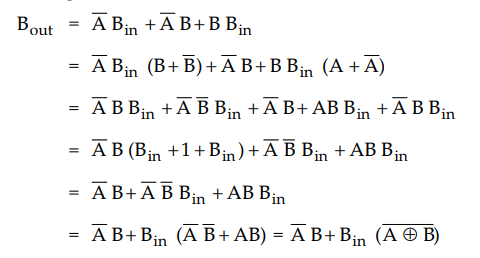
• This Boolean function is same as borrow out of the full-subtractor. Therefore, we can implement full-subtractor using two half-subtractors and OR gate.

Review Questions

1. Define half subtractor and full subtractor.

2. Explain the operation of a half subtractor with the help of logic diagram and truth table.

3. Realize full-subtractor using K-map.

4. Design full-subtractor circuit and draw necessary truth tables.

5. Explain how full subtractor can be designed by using two half subtractor circuits. Draw the circuit diagram.

6. Design a full subtractor and implement it using logic gates.

7. Design a full subtractor and realise using logic gates. Also, implement the same using half subtractors.

AU : Dec.-16, Marks 13