Synchronizing Current and Synchronizing Power

Synchronizing Current and Synchronizing Power

After proper synchronization of the alternators, they will run in synchronism. A synchronizing torque will be developed if any of the alternator drops out of synchronism and will bring it back to the synchronism.

1. Two Alternators in Parallel

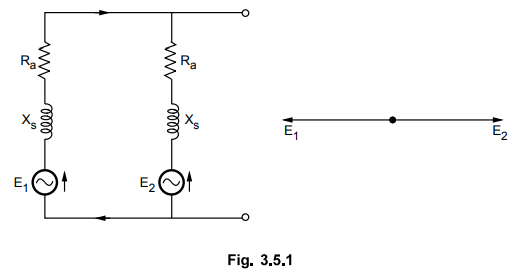
Consider the two alternators shown in the Fig. 3.5.1 which are in exact synchronism. Due to this they are having same terminal p.d. and with reference to their local circuit they are in exact phase opposition. So there will not be any circulating current in the local circuit. The e.m.f. E₁ of alternator 1 is in exact phase opposition to that of alternator E2.

With respect to external load, the e.m.f.s of the two alternators are in the same direction although they are in phase opposition with reference to local circuit. There will be no resultant voltage in the local circuit.

Now assume that speed of alternator 2 is changed such that its e.m.f. E₂ falls by an angle a . But E_x and E₂ are equal in magnitude. The resultant voltage Er in this case will cause a current in the local circuit which is called synchronizing current. This circulating current is given by,

I_SY = E_r / Z_s

where          Z_s = Synchronous impedance of windings of alternator 

The phase angle of I_SY is given by an angle θ which can be computed as tan θ = Xs/R_a where X_s is synchronous reactance and R_a is armature resistance. This angle is almost 90°.

Thus I_SY lags E_r by almost 90° and approximately in phase with E₁. This current is generating current with respect to alternator 1 since it is in the same direction as that of e.m.f. of alternator 1 while it will be motoring current for alternator 2 as it is in the opposite direction as that of e.m.f. of alternator 2. This current I_SY will produce a synchronizing torque which will try to retard alternator 1 whereas accelerate the alternator 2.

The power output of alternator 1 supplies power input to alternator 2 and copper losses in the local path formed by armatures of two alternators.

Power output of alternator 1 – E₁ I_SY cos ϕ₁

This power is approximately equal to E₁ I_SY  as cos ϕ₁ is small and is almost in phase with E₁. This power is called synchronizing power. Similarly power input to alternator 2 is E₂ I_SY cos ϕ₂ which is equal E₂ I_SY as ϕ₂ is also small.

E₁ I_SY = E₂ I_SY  + Cu losses in the local circuit

Let     E₁ = E₂ = E

Let the magnitude of resultant e.m.f. be Er which is given by,

E_r = 2 E cos(180^o - ɑ / 2) = E cos (90^o - ɑ) = 2 E sin (ɑ/2)

But ɑ is small    sin ɑ/2 = ɑ/2

E_r = 2 E (ɑ/2) = ɑ E …[0 = 90^o, sin θ = 1]

The electrical angle ɑ is expressed in radians.

If R_a is not assumed as negligible then θ will not be 90° so the above expression can be written in exact form as

P_SY = ɑ E² / 2X_S sin θ

For 3 phases, total synchronizing power is given by,

P_SY = 3ɑ E² / 2X_S sin θ

The above expression is valid for two alternators connected in parallel and operating at no load.

2. Alternator Connected to Infinite Bus

Now let us consider the case of alternator connected to infinite bus bar (the concept of infinite bus bar is explained later) then the above expression for synchronizing power is still valid with the change of reactance of only one alternator is considered instead of two alternators.

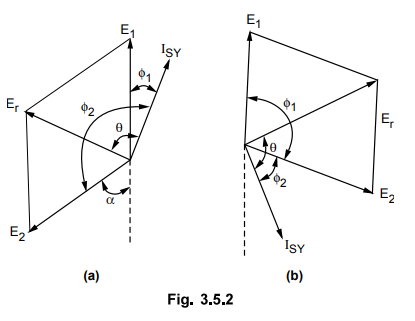
 Now assuming that E2 has advanced in phase shown in the Fig. 3.5.2 (b).

The synchronizing current ISY in this case will be generating current for machine 2 and motoring current for machine 1. This will again produce a torque which will try to accelerate alternator 1 and try to retard alternator 2.

Key Point : Hence if synchronism between the two machines is lost then synchronizing current will flow in the local circuit which will produce a synchronizing torque.

This torque will tend to accelerate the lagging machine while will try to retard the leading machine. In case of machines which are loaded this current is superimposed on the load current.

Review Questions

1. Explain the significance of synchronizing power in case of an alternator connected to an infinite bus bar.

2. What is synchronising power ? Derive an expression for the synchronising power between the two alternators connected in parallel.