Theory of Cylindrical Rotor Machines

Theory of Cylindrical Rotor Machines

Let us consider the phasor diagram for alternator for lagging p.f. as shown in the Fig. 3.6.1.

Let E = E.M.F induced in each phase

V = Terminal voltage

ϕ = Phase angle between voltage and current

δ = Power angle

R_a = Resistance of armature

X_s = Synchronous reactance of alternator

Key Point : With increase in δ, power increases and with decrease in 8, power decreases. Power in case of synchronous machine depends on the angle δ. This angle δ is called power angle.

In case of large synchronous machines, X_s >>> R_a

θ = tan^-1(X_s/R_a) ≈ 90° (if armature resistance is neglected)

Substituting θ = 90°, in above equation the net electrical power output from alternator is given by,

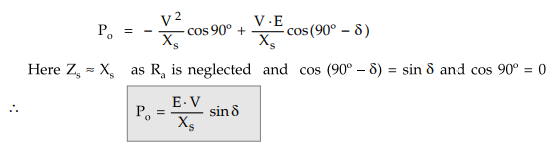
1. Maximum Power Output

Now let's find the maximum power output developed by alternators by taking derivative of Po w.r.t 8 and equating it to zero to get the condition for maximum power.

Substituting this condition for maximum power in the expression for output power,

2. Power Factor at Maximum Power Condition

Consider the phasor diagram as shown in the Fig. 3.6.2.

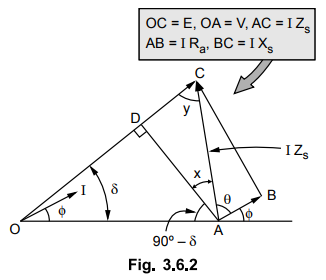
For P_omax, θ  = δ and cos ϕ is leading hence I leads V by ϕ.

AD is perpendicular drawn from A on OC. In triangle OAD,

This is the leading power factor at the time of maximum power condition.

3. Operating Characteristics

The operating characteristics of a synchronous machine are seen under variable excitation and load condition. One of the parameter is kept constant while other is varied for studying these characteristics. The resistance of armature is neglected as it does not change the characteristics significantly. So the corresponding circuit is as shown in the Fig. 3.6.3.

The phasor diagram corresponding to above condition is shown in the Fig. 3.6.4.

Power delivered to the infinite bus per phase is given by,

P_i = V – I_a cos ϕ

From the above phasor diagram it can be seen that

∠ OBA = 90 - ϕ

∠ OBC = 180 - (90 - ϕ) = 90 + ϕ

From ∆ OBC,

Key Point : The above power is the electrical power exchanged with bus bars. Angle 8, between E and V is known as power angle.

4. Power Angle Characteristics

As seen previously,

P_i = EV sin δ / X_s

The relationship between P_i and δ is known as power angle characteristics of the machine. It is shown in the Fig. 3.6.5.

The maximum power occurs at δ = 90°. Beyond this point the machine falls out of step and loses synchronism. The machine can be taken upto      P_imax only by gradually increasing the load. This is known as the steady state stability limit of the machine. The machine is normally operated at 8 much less than 90°.

Example 3.6.1. A 20 MVA, 3 phase star connected alternator with an impedance of 5 Ω and a resistance of 0.5 Ω is operating in parallel with constant voltage 11 kV busbars. If its field current is adjusted to give an excitation voltage of 12 kV, calculate :

1) The maximum power output from the alternator and

2) The power factor under maximum conditions.

Solution : MVA rating of alternator is 20 MVA.

Example for Practice

Example 3.6.2 For a cylindrical rotor alternator working at lagging power factor, show that tan δ = I_a(X_scos ϕ - R_asin ϕ) / V_t + I_a(X_s sin ϕ + R_a cos ϕ)

The symbols having their usual meanings.

Review Question

1. Derive the expression for the output power of cylindrical rotor alternator connected to infinite bus in terms of excitation voltages, bus bar voltage and load angle.