Three phase power measurement - two-watt meter method

THREE PHASE POWER MEASUREMENT - TWO-WATT METER METHOD

This method is applied usually for measuring the electrical power in 3-phase, 3-wire circuit. The load may be balanced or unbalanced. It may be connected either in delta or star.

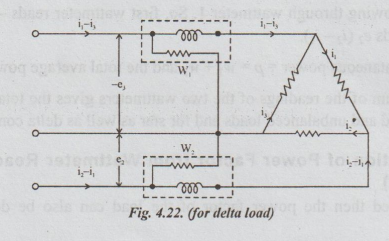
The current coils of 2 watt meters are inserted in two of the lines and voltage coil of each wattmeter is connected from its own current coil to the line in which no wattmeter has been connected. The connections of watt meters in this method are shown in Fig.4.21 & 4.22.

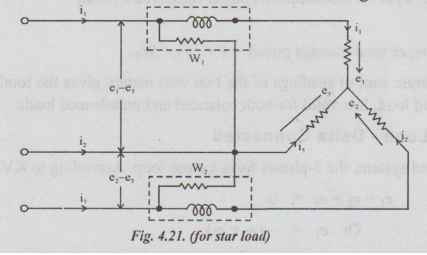
Let e₁, e₂ and e₃ be the voltages of the three loads at particular instant and i, iz and is be the currents of the three loads i.e., these voltages and currents are called instantaneous values. Hence, the power at the instant under consideration is equal to the sum of their products, regardless of power factor

i.e., Instantaneous power = P = e₁i₁ + e₂i₂ + e₃i₃ ... (1)

1. Case (1) Load Star Connected

Since all the three-phases meet at a star point, application of KCL yields

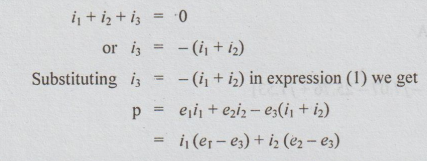
Here i₁ = the instantaneous current flowing through the current coil of wattmeter. (e₁ - e₃) = the instantaneous potential difference across voltage coil of wattmeter 1.

Therefore i (e₁- e₃) = w₁. w₁ is the instantaneous power measured by wattmeter 1.

I₂ = The instantaneous currents flowing through the current coil of wattmeter 2. (e₂- e₃) = the instantaneous potential difference across the voltage coil of wattmeter 2.

I₂ (e₂ – e₃) = w₂. W₂ is the instantaneous power measured by watt meter 2.

Hence p = w₁ + w₂ or total average power = P = W₁ + W₂.

Hence, the algebraic sum of readings of the two watt meters gives the total power in the 3-phase, 3-wire star connected load. It is valid for both balanced and unbalanced loads.

2. Case (2) Load - Delta Connected

In delta connected system, the 3-phases form a close loop. According to KVL,

e₁ + e₂ + e₃

Or e₁ = -(e₂ + e₃ )

From equation (1),

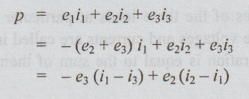
- e₃ is the instantaneous p.d. across the voltage coil of wattmeter 1.

(i₁ – i₃ ) the current flowing through wattmeter 1. So, first wattmeter reads - e3 (i - i3). Similarly, the second wattmeter reads e₂ (i₂ - i₁).

Hence, the total instantaneous power = p = w₁ + w₂ and the total average power = P = W₁ + W₂.

Thus, the algebraic sum of the readings of the two wattmeters gives the total power of the circuit. It is true for both balanced and unbalanced loads and for star as well as delta connected systems.

3 (a) Determination of Power Factor from Wattmeter Readings (Valid Only for Balanced Loads)

If the load is balanced then the power factor of the load can also be determined from the 2 wattmeter readings.

The vector diagram for a balanced star connected inductive load is shown in Fig.(4.23)

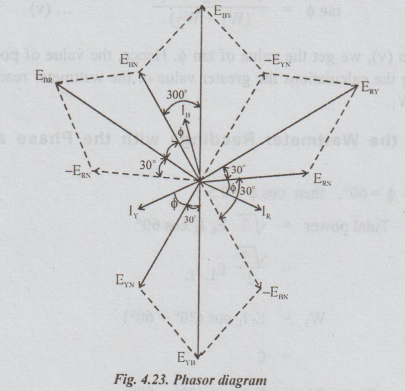
The circuit coil of wattmeter 1 is connected in R-phase. The voltage coil of wattmeter 1 is connected between R - phase and Y - phase.

Reading of wattmeter 1 = W₁.

= |E_RY| I_R × cosine of the angle between E_RY and I_R

W₁ = E_RY. I_R COS (30+ϕ)

= E_L. I_L cos (30+ϕ) ... (i)

The current coil of wattmeter 2 is connected in B-phase. Voltage coil of wattmeter 2 is connected between B and R-phases. The angle between EBR and I, is equal to (30+ϕ)

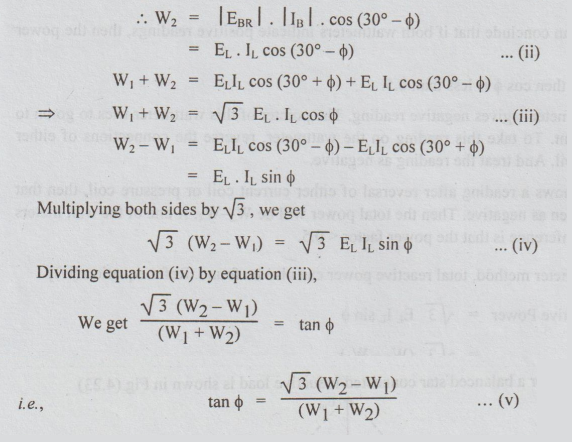
From the equation (v), we get the value of tan o. Hence, the value of power factor cos o can be calculated. In making the calculations the greater value of the wattmeter readings is usually taken as W₂ and the other as W₁.

(b) Variation of the Wattmeter Readings with the Phase angle & and hence Cosϕ

Case (1): When ϕ = 60°, then cos ϕ = 0.5

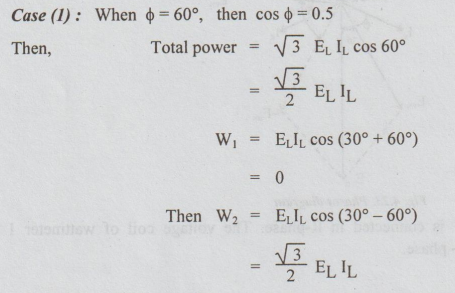
Hence one wattmeter will read zero and the other will read the total power. In other words, we can conclude as below:

In the 2 wattmeter method, if one of the wattmeters reads zero reading, the power factor must be 0.5. Here we assume that both wattmeters are fault - free.

Case (2): if ϕ < 60°. Then cos o is more than 0.5. In this case, both watt meters indicate positive readings.

In other words, we can conclude that if both wattmeters indicate positive readings, then the power factor is more than 0.5.

Case (3): If ϕ > 60°, then cos o is less than 0.5.

In this case, the wattmeter 1 gives negative reading. The pointer of this wattmeter tries to go on to the left side of zero point. To take this reading on the wattmeter, reverse the connections of either current coil or voltage coil. And treat the reading as negative.

i.e., If wattmeter I shows a reading after reversal of either current coil or pressure coil, then that watt meter reading is taken as negative. Then the total power will be W2-W1. If one of the watt meters reads negative then the inference is that the power factor < 0.5.

[Note: In the 2 wattmeter method, total reactive power can also be found. Refer equation (iv)]

Total reactive Power = √3 E_L I_L sin

= √3 (W₂ – W₁)