Tight binding approximation

TIGHT BINDING APPROXIMATION

In solid, ionic cores at fixed lattice locations and free electron gas enveloping these ionic cores.

In other words, it is assumed that the solid already exists. The ionic cores are 'tightly bound' to their lattice locations. The electrons are 'free' to run through the extent of the solid. This is called the 'Free electron approximation'.

There is another approach to modeling materials which starts from opposite position.

In this approach, the atoms are independent to begin with and they are brought together to build the solid. The electrons are bound to their respective individual atoms to begin with.

In this case the atoms are free to begin with while the electrons are tightly bound to the atom.

• In view of the electronic properties of the materials, this approach is referred to as the "Tight binding approximation' highlighting the status of the electrons at the start of the model.

•  Figure 2.20 shows how the tight binding approximation builds the band structure of the solid.

• When the atoms are far apart, all the bound electrons associated with each atom, have fixed energy levels.

Assuming that building the solid starts using atoms of the same element. Thus, the energy levels occupied by the respective electrons in each atom will be identical.

• As we bring the atoms close to each other to form the anonibel solid, the electrons will still maintain their original energy levels as long as the interatomic seperation is large.

• When the atoms get close enough, the outer shell electrons begin to overlap with each other.

• The energy levels of these outer shell electrons are forced to split into energy levels above and below the energy level of these electrons when they belong to individual atoms.

• The splitting of energy levels occurs because electrons obey the Pauli's exclusion principle.

• Initially only the outer shell electrons overlap, therefore only their levels split. But inner shell electrons still maintain their energy levels like individual atom.

• If the interatomic separation keeps decreasing even further, progressively more of the inner shell electron levels will overlap and hence also split.

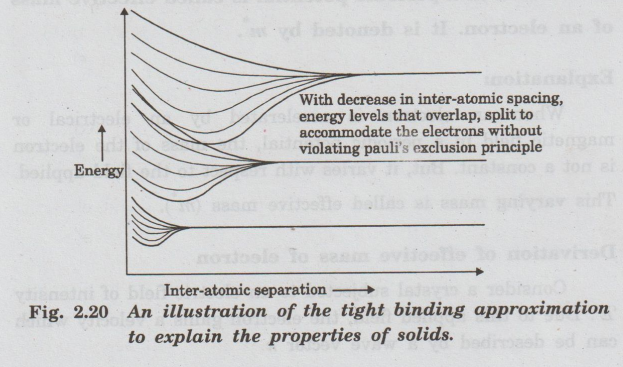
• At each energy level, the level will split to enough new benigno energy levels (band) so as to accommodate the electrons zinois of all the atoms in the solid taken together.

• For for example, if hundred atoms come together, and there is one electron in the outer shell, the solid will split the energy level to a hundred energy levels. Thus the hundred outer shell electrons are filled corresponding to the combined solid.

•  In view of the starting points, the free electron approximation lends itself more easily to the treatment of metallic system. The tight binding approximation is typically more consistent with the state of the material in the case of insulators, so it is better suited for modeling insulators.