Torque and Speed Equations

Torque and Speed Equations

AU: Oct.-98, April-99, Dec.-05, 06,13,19 May-07, 08,09,11,15,17,19

• Before analyzing the various characteristics of motors, let us revise the torque and speed equations as applied to various types of motors.

T α ϕ I_{a ...................}From torque equation

• This is because, 0.159  PZ / A is a constant for a given motor.

Now, ϕ is the flux produced by the field winding and is proportional to the current passing through the field winding.

Φ α I_field

• But for various types of motors, current through the field winding is different. Accordingly torque equation must be modified.

• For a d.c. shunt motor, I_sh is constant as long as supply voltage is constant. Hence flux ϕ is also constant.

T α I_a for shunt motors.

For a d.c. series motor, Ise is same as I_a. Hence flux ϕ is proportional to the armature current I_a.

T ∝ I_a  ϕ ∝ I_a²  for series motors.

Similarly as Eb = ϕPNZ / 60 A, we can write the speed

equation as,

Eb ∝ ϕ N

N ∝ E_b / ϕ

• These relations play an important role in understanding the various characteristics of different types of motors.

1. Speed Regulation

• The speed regulation for a d.c. motor is defined as the ratio of change in speed corresponding to no load and full load condition to speed corresponding to full load.

Mathematically it is expressed as,

% Speed regulation = N_{no load} -N_{full load} / N_{full load} × 100

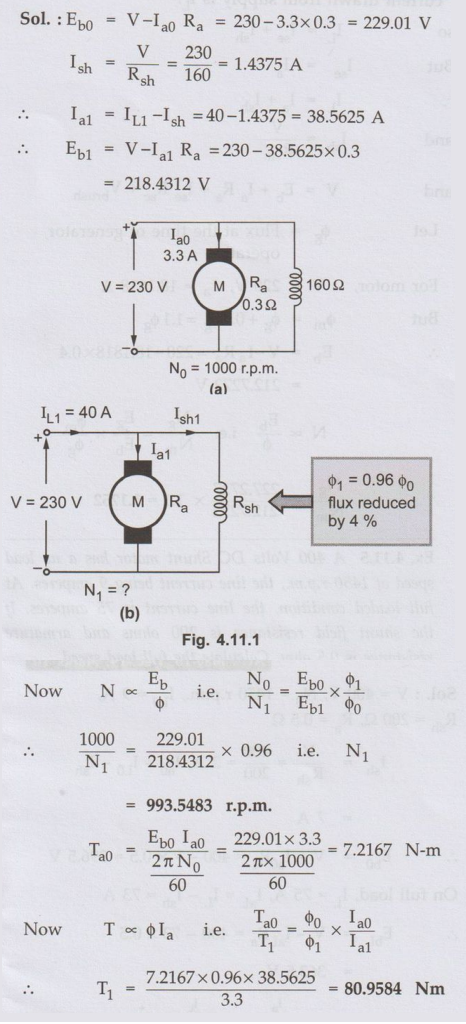
Ex. 4.11.1 A 230 V d.c. shunt motor, takes an armature current of 3.33 A at rated voltage and at no load speed of 1000 r.p.m. The resistances of the armature circuit and field circuit are 0.3 Ω and 160 Ω respectively. The line current at full load and rated voltage is 40 A. Calculate, at full load, the speed and the developed torque in case the armature reaction weakens the no load flux by 4 %..

AU: Dec.-06, Marks 8

Sol. :

Ex. 4.11.2 A 220 V shunt motor has an armature resistance of 0.5 Ω and takes an armature current of 40 A on a certain load. By how much must the main flux be reduced to raise the speed by 50 % if the developed torque is constant? Neglect saturation and armature reaction.

AU: May-08, Marks 8

Sol. :

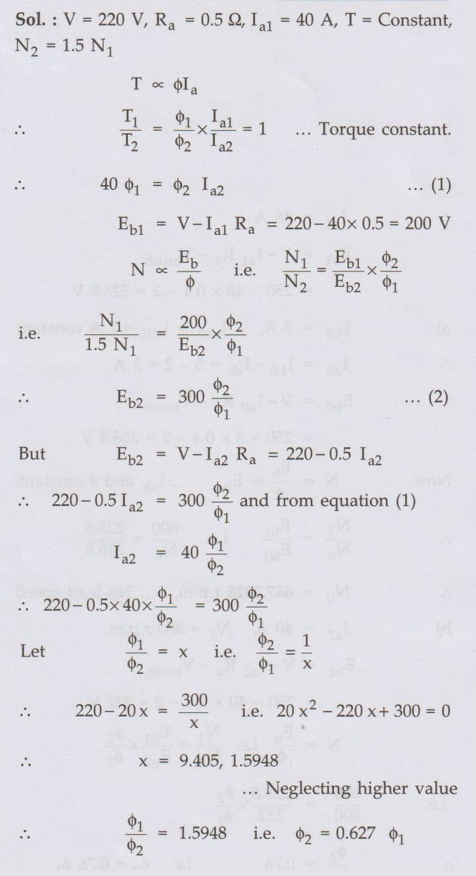
Ex. 4.11.3 A shunt motor runs at 600 r.p.m. from 250 V supply and takes a line current of 50 A. Its armature and field resistances are 0.4 Ω and 125 Ω respectively. Neglecting the effects of armature reaction and allowing 2 V brush drop. Calculate

1) The no load speed if the no load line current is 5 A. 2) The percentage reduction in flux per pole in order that the speed may be 800 r.p.m. when the armature current is 40A. AU: Dec.-05, May-09, 17, Marks 8

Sol.

Thus the flux must be reduced by 100 – 76 = 24 % to achieve change in speed from 600 r.p.m. to 800 r.p.m.

Ex 4.11.4 A 220 V d.c. generator supplies 4 kW at a terminal voltage of 220 V, the armature resistance being 0.4 Ω. If the machine is now operated as a motor at the same terminal voltage with the same armature current, calculate the ratio of generator speed to motor speed. Assume that the flux/pole is made to increase by 10% as the operation is changed over from generator to motor.

AU: May-11, Marks 6

Sol.

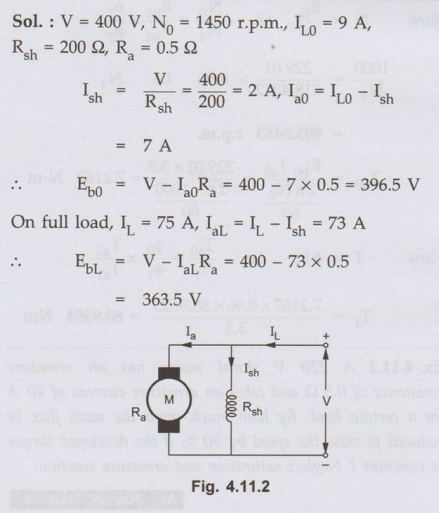
Ex. 4.11.5 A 400 Volts DC Shunt motor has a no load speed of 1450 r.p.m., the line current being 9 amperes. At full loaded condition, the line current is 75 amperes. If the shunt field resistance is 200 ohms and armature resistance is 0.5 ohm. Calculate the full load speed.

AU May-15, Dec.-19, Marks 10

Sol. :

Ex. 4.11.6 A d.c. series motor is running with a speed of 800 r.p.m. while taking a current of 20 A from the supply. If the load is changed such that the current drawn by the motor is increased to 50 A, calculate the speed of the motor on new load. The armature and series field winding resistances are 0.2 Ω and 0.3 Ω respectively. Assume the flux produced is proportional to the current. Assume supply voltage as 250 V.

Sol.:

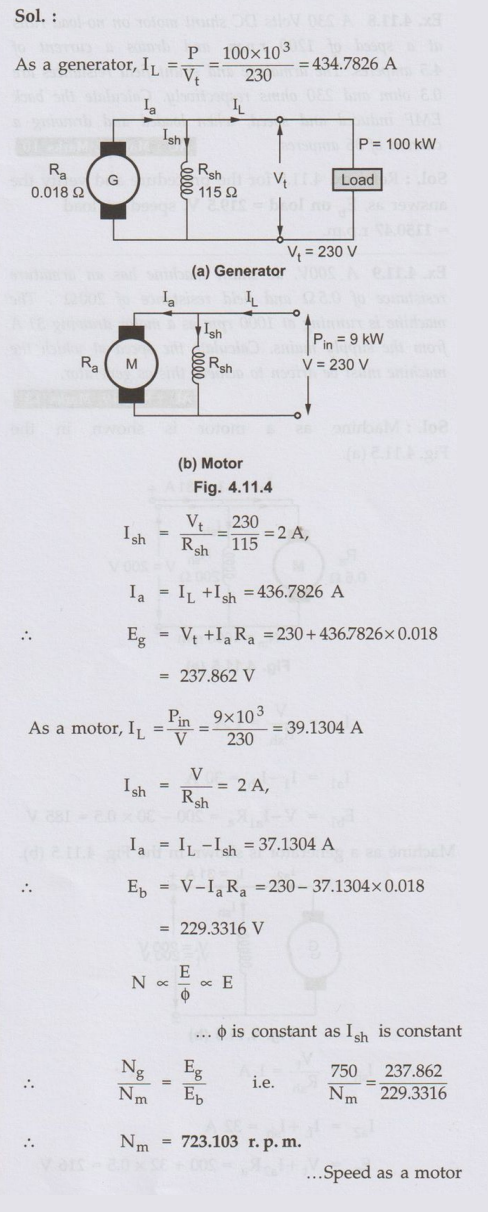
Ex. 4.11.7 A 100 kW dc shunt generator driven by a belt from an engine runs at 750 rpm and is connected to 230 V dc mains. When the belt breaks, it continues to run as a motor drawing 9 kW from the mains. At what speed would it run? Given: Armature resistance = 0.018 Ω and field resistance = 115 Q.

AU: Dec.-13, Marks 16

Sol.:

Ex. 4.11.8 A 230 Volts DC shunt motor on no-load runs at a speed of 1200 r.p.m. and draws a current of 4.5 amperes. The armature and shunt field reistances are 0.3 ohm and 230 ohms respectively. Calculate the back EMF induced and speed, when loaded and drawing a current of 36 amperes. AU May-15, Marks 10

Sol. Refer ex. 4.11.5 for the procedure and verify the answer as, E_b on load = 219.5 V, speed on load = 1150.47 r.p.m.

Ex. 4.11.9 A 200V, dc shunt machine has an armature resistance of 0.5 Ω and field resistance of 200 Ω. The machine is running at 1000 rpm as a motor drawing 31 A from the supply mains. Calculate the speed at which the machine must be driven to achieve this as generator.

AU: May-19, Marks 13

Sol. :

Machine as a motor is shown in the Fig. 4.11.5 (a).

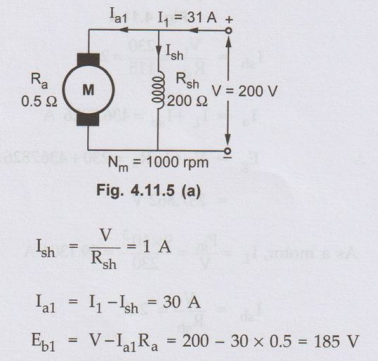
Machine as a motor is shown in the Fig. 4.11.5 (b).

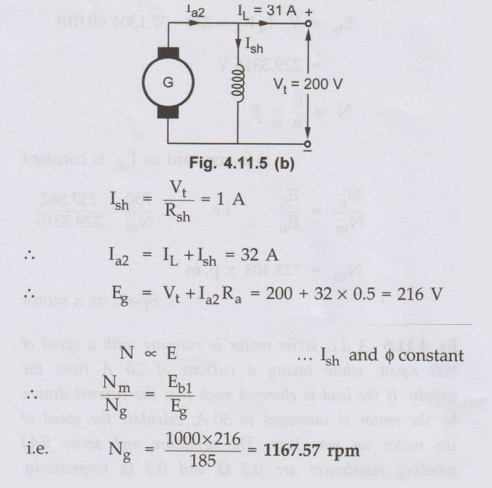
Review Questions

1. A d.c. series motor developing 40 Nm torque is subjected to the conditions that make field flux to decrease by 30 % and armature current to increase by 15%. Calculate the new torque. AU: Oct.-98

(Ans.: 32.2 Nm)

2. A 250 V d.c. _shunt motor runs at 1000 r.p.m. on no load and takes 5 A. The armature and shunt field resistances are 0.2 Ω and 250 Ω respectively. Calculate the speed when loaded and taking a current of 50 A. Due to armature reaction the field weakens by 3%. AU: April-99, May-07 

(Ans.: 993.695 r.p.m.)

3. A 120 V d.c. shunt motor has an armature resistance of 0.2 Ω and a field resistance of 60 Ω. It runs at 1800 r.p.m. taking a full load current of 40 A. Find the speed on half load condition. 

(Ans. 1860.85 r.p.m.)

4. A 250 V d.c. shunt motor has R_a = 0.08 Ω When connected to 250 V d.c. supply it develops back e.m.f. of 242 V at 1500 r.p.m. Determine

i) Armature current ii) Armature current at start iii) Back e.m.f. if armature current is changed to 120 A iv) The speed of the machine if it is operated as a generator in order to deliver an armature current of 87 A at 250 V.

(Ans. 100 A, 3125 Amp, 240.4 V, 1592.7 r.p.m.)

5. A 4 pole, 250 V d.c. shunt motor takes 4 A on no load, running at 1200 r.p.m. The armature resistance is 0.1 Ω and shunt field resistance is 125 Ω. Total brush drop is 2 V. If it takes total current of 61 A on full load, calculate its full load speed. Assume that flux gets weakened by 5% on full load condition due to armature reaction. 

(Ans. 1234.102 r.p.m.)

6. The full load output power of a d.c. shunt motor is 16 kW while connected to 250 V supply. Calculate the value of the starter resistance necessary to limit the starting current to 1.5 times the full load current. The full load efficiency of the motor is 80 % and resistance of the armature circuit is 0.18 Ω. Neglect shunt field current. Also calculate the back e.m.f. of the motor when the current has fallen to the full load value, assuming whole of the starter resistance still in the circuit. 

(Ans.: 1.90332, 83.33 V)