Electrical Machines: Unit III: a. D.C. Motors
Torque Equation of a D.C. Motor
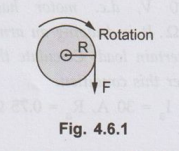
• It is seen that the turning or twisting force about an axis is called torque. Consider a wheel of radius R metres acted upon by a circumferential force F newtons as shown in the Fig. 4.6.1.
Torque
Equation of a D.C. Motor
AU: May-07,08,09,14,16, April-04,
Dec.-07.09,14
•
It is seen that the turning or twisting force about an axis is called torque.
Consider a wheel of radius R metres acted upon by a circumferential force F
newtons as shown in the Fig. 4.6.1.
The
wheel is rotating at a speed of N r.p.m.
The angular speed of the wheel is,

•
Let Ta be the gross torque developed by the armature of the motor.
It is also called armature torque. The gross mechanical power developed in the
armature is Eb Ia, as seen from the power equation. So if
speed of the motor is N r.p.m. then,
Power
in armature = Armature torque × ω
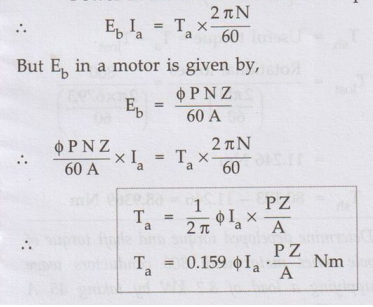
This
is the torque equation of a d.c. motor.
Ex. 4.6.1 A 4 pole d.c. motor takes a 50 A
armature current. The armature has lap connected 480 conductors. The flux per
pole is 20 mWb. Calculate the gross torque developed by the armature of the
motor.
AU: Dec.-07, Marks 8
Sol. :
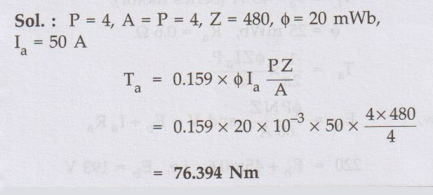
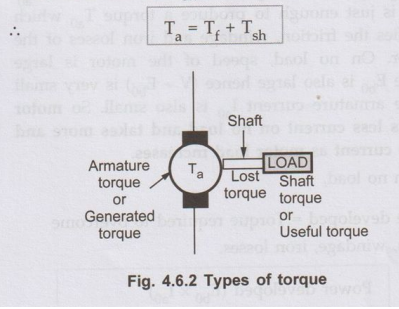
1. Types of Torque in the Motor
•
Basically the torque is developed in the armature and hence gross torque
produced is denoted as Ta.
•
The mechanical power developed in the armature is transmitted to the load
through the shaft of the motor. is impossible to transmit the entire power
developed by the armature to the load. This is because while transmitting the
power through the shaft, there is a power loss due to the friction, windage and
the iron loss. The torque required to overcome these losses is called lost
torque, denoted as T. These losses are also called stray losses.
•
The torque which is available at the shaft for doing the useful work is known
as load torque or shaft torque denoted as Tsh.
Ta = Tf + Tsh
•
The shaft torque magnitude is always less than the armature torque, (Tsh
< Ta).
•
The speed of the motor remains same all along the shaft say N r.p.m. Then the
product of shaft torque Te and the angular speed o rad/sec is called power
available at the shaft i.e. net output of the motor. The maximum power a motor
can deliver to the load safely is called output rating of a motor. Generally it
is expressed in H.P. It is called H.P. rating of a motor.
Net
output of motor = Pout =Tsh × ω
2. No Load Condition of a Motor
•
On no load, the load requirement is absent. So Tsh = 0. This does
not mean that motor is at hault. The motor can rotate at a speed say N0
r.p.m. on no load. The motor draws an armature current of Ia0.
Ia0
=V-Eb0 / Ra
where
Eb0 is back e.m.f. on no load, proportional to speed N0.
Now
armature torque T for a motor is,
Ta α ϕ Ia
As
flux is present and armature current is present, hence Ta0 i.e.
armature torque exists on no load.
Now
Ta = Tf + Tsh
But
on no load,Tsh = 0
Ta0
= Tf
•
So on no load, motor keeps on rotating at a speed of N0 r.p.m. drawing
an armature current of Ia0 This is just enough to produce a torque Ta0
which satisfies the friction, windage and iron losses of the motor. On no load,
speed of the motor is large hence Ebo is also large hence (V – Eb0)
is very small hence armature current Ia0 is also small. So motor
draws less current on no load and takes more and more current as motor load
increases.
So
on no load,
Torque
developed = Torque required to overcome friction, windage, iron losses.
Power
developed (Eb0× Ia0) = Friction, windage and, iron
losses.
where
Eb0 = Back e.m.f. on no load
and Ia0 = Armature current drawn on no
load
•
This component of stray losses i.e. Eb0 La0 is
practically assumed to be constant though the load on the motor is changed from
zero to the full capacity of the motor. So Tf is practically assumed
constant for all load conditions.
Ex. 4.6.2 A 4 pole, 220 V d.c. shunt motor,
lap wound has 960 conductors. The flux per pole is 20 mWb. Determine the torque
developed by the armature and the useful torque in Nm when the current drawn by
the motor is 28 A. The armature resistance is 0.1 Ω and the shunt field
resistance is 125 Ω. The rotational losses of the machine amounts to 800 watts.
AU: Dec.-07, Marks 8
Sol.

Ex 4.6.3 Determine
developed torque and shaft torque of 220 V, 4 pole series motor with 800
conductors wave connected supplying a load of 8.2 kW by taking 45 A from the
mains. The flux per pole is 25 mWb and its armature circuit resistance is 0.6 Ω.
AU: May-08, Marks 8
Sol. :

Ex. 4.6.4 A 60 kW, 400 V d.c. shunt motor has
4 poles and a wave connected armature of 450 conductors. The flux per pole is
45 mWb. Ra = 0.1Ω and Rsh = 200 Ω.If the full load efficiency
is 90.5 %, find the 1) Speed 2) Armature torque 3) Useful torque. AU: May-09, Marks 8
Sol. :

Ex. 4.6.5 A 4 pole dc motor is lap wound with
400 conductors. The pole-shoe is 20 cm long and the average flux density over
one- pole- pitch is 0.4 T, the armature diameter being 30 cm. Find the torque
and gross mechanical power developed when the motor is drawing 25 A and running
at 1500 rpm.
AU: May-16, Marks 8
Sol. :

Review Questions
1. Derive from the
first principle an expression for the torque developed in a d.c. motor. AU: May-07, 08, 09,
14, Dec.-09, 14, Marks 8
2. A 200 V, 4 pole, lap wound, d.c. shunt motor has 800 conductors on its armature. The resistance of the armature winding is 0.5 Ω and that of shunt field winding is 200 Ω. The motor takes a current of 21 A, the flux per pole 30 mWb. Find the speed and the gross torque developed in the motor.
(Ans. 475 r.p.m., 76.38 N-m)
3. A d.c. motor takes
an armature current of 74 A when flux is 10 mWb. It develops a torque of 120
N-m. If armature current is changed to 45 A keeping the flux constant,
determine the new torque developed. With the same flux, if entire load on the
motor is removed, armature current is observed to be 6.8 A. Determine the
torque required to overcome stray losses.
(Ans. 72.97 N-m,
11.02 N-m)
4. A 4 pole d.c. motor takes an armature
current of 50 Amps. The armature has lap connected 480 conductors. The flux per
pole is 20 mWb. Calculate the gross torque developed by the motor. AU: April-04 (Ans.:
76.3943 N-m)
5. A 4 pole, lap
wound d. C. motor has 540 conductors. Its speed is found to be 1000 r.p.m. when
it is made to run light. The flux per pole is 25 mWb. It is connected to 230 V
d.c. supply. The armature resistance is 0.8Ω. Calculate i) Induced e.m.f. ii)
Armature current iii) Stray losses iv) Lost torque.
W 8810.0 [Ans.: 225
V, 6.25 A, 1406.25 W, 13.428 Nm]
6. Determine the torque developed when a current of 30 A passes through the armature of a motor with lap winding of 310 conductors, 4 pole with pole shoes 16.2 cm long and subtending angle of 60° at the centre. The bore radius is 16.2 cm and flux density in the air gap is 0.7 T.
[Ans.: 28.44 Nm]
Electrical Machines: Unit III: a. D.C. Motors : Tag: : - Torque Equation of a D.C. Motor
Related Topics
Related Subjects
Electrical Machines I
EE3303 EM 1 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
