Two Mark Question and Answers set - 5

101. When do the two wattmeters read equal in the two wattmeter method of three-phase power measurement ?

Ans: When the power factor is unity, both wattmeters will indicate equal readings.

 

102. How can a wattmeter be used to measure reactive power?

Ans: In case of balanced three-phase circuit, the reactive power can be determined by using one wattmeter. The current coil of the wattmeter is connected in one line and its pressure coil is connected across the other two lines.

Let the reading of wattmeter be W_r

Then the total reactive power = √3 W_r

 

103. When does one wattmeter read zero in the two-wattmeter method of three-phase power measurement?

Ans: When the power factor is 0.5, one of the wattmeters indicates zero reading.

 

104. Give the three-phase power expression in terms of phase values.

Ans: Total average power = 3 | Vϕ | Iϕ | cos ϕ

where, Vϕ = phase voltage

Iϕ = phase current

cos ϕ = power factor.

ϕ = angle between phase voltage and phase current

 

105. What are coupled circuits?

Ans: Two circuits are said to be coupled, when atleast a part of the electrical energy supplied to one circuit is transferred to the other.

 

106. Define self-inductance. What is its unit?

Ans: The self-inductance of a coil is defined as the flux linkage in that coil per unit current in itself. Its unit is henry.

i.e., L = Nϕ / I

where N is no. of turns, ϕ is the flux in webers and I is the current in amperes.

L is also defined as weber turns per ampere current in the same coil.

 

107. Write the expression for effective inductance of the series connected magnetically coupled coils.

Ans: For cumulative coupling,

effective inductance L = L₁ + L₂ + 2M

For differential coupling,

total inductance L = L₁ + L₂ - 2M

where L₁, L₂ are self inductances of the two coils. M is the mutual inductance between the two. L is the effective inductance.

 

108. The effective inductance of the parallel connected magnetically coupled coils is less for differential connection than cumulative one. State True or False.

Ans: True.

 

109. Give the expression for critical coefficient of coupling for a singly tuned circuit.

Ans: 1 / √ Q₁ Q₂

Here, Q₁, Q₂ are quality factors of primary and secondary windings of single tuned circuits.

 

110. Define coefficient of Coupling.

Ans: Coefficient of coupling is defined as ratio of mutual inductance to the geometric mean of the self inductances. i.e.,

K = M / √L₁ L₂

It is also defined as follows. Let there be two coils coupled magnetically. Let the flux produced in coil 1 be 1, when the coil 1 is excited by a voltage source. Let 12 be the flux linked in coil 2.

So, K = ϕ₁₂ / ϕ₁ also K = ϕ₂₁ / ϕ₂

 

111. What is meant by double tuned coupled circuits?

Ans: A double tuned coupled circuit is one in which the capacitor is present in both primary and secondary circuits.

It may be a series double-tuned or parallel-double-tuned. A series doubly tuned transformer has a series capacitor in the primary winding and has a capacitor connected in parallel across the secondary.

A parallel doubly tuned transformer has a capacitor connected in parallel with the primary winding and a capacitor in parallel with the secondary winding.

 

112. What is the maximum possible mutual inductance of two inductively coupled coils, with self-inductances L₁ = 25 mH, L₂ = 100mH?

Ans:

maximum M = √L₁ L₂

= √25 × 10^-3 × 100 × 10^-3

= √25 × 10^-4

= 50 mH

 

113. Two inductors are connected as shown in the figure. What is the value of the effective inductance of the combination?

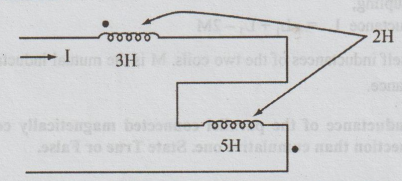
Ans: The current is entering one coil at the dot and leaving the other coil at the dot. So, the coupling is differential.

The effective inductance = L₁ + L₁  - 2M

= 3 + 5 - 2(2)

= 4 Henrys

 

114. Define mutual inductance and write an expression for it.

Ans: The mutual inductance is defined as the ability of one coil to produce emf in second coil, by induction when the current flows in the first coil. This action is reciprocal. It is quantitatively measured in terms of coefficient of mutual inductance. M is defined as weber turns in one coil per ampere current in the other coil.

i.e., M = N₂ ϕ₂ / I₁ = N₁ ϕ₁ / I₂ Henrys

115. Give the applications of double-tuned circuits.

Ans: It is widely used in the intermediate frequency amplifiers in receivers.

 

116. State the dot rule for coupled circuit.

Ans:

1. If both currents enter dotted ends of coupled coils or if both currents enter undotted ends, then the signs on the M-terms will be same as the signs on the L-terms.

2. If one current enters a dotted end and the other an undotted end, the signs on the M-terms will be opposite to the signs on the L-terms.

 

117. Sketch the frequency response of double-tuned circuit.

Ans:

 

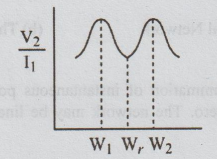
118. Define critical coupling.m

Ans: Critical coupling is given by

K_C = M_c / √ L₁ L₂

Here M_c is called critical value of mutual inductance. At this value of mutual inductance, the output voltage or voltage amplification in a double tuned coupled circuit is maximum.

 

119. Sketch the frequency response of a single tuned circuit.

Ans:

 

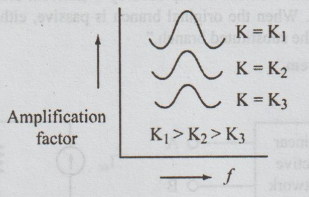
120. State superposition theorem.

Ans: "In a linear circuit containing more than one source, the current that flows at any point or the voltage that exists between any two points is the algebraic sum of the currents or the voltages that would have been produced by each source taken separately with all other sources removed."

 

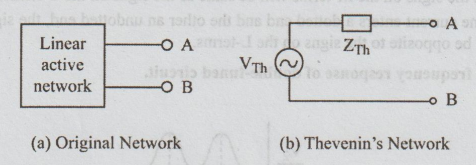
121. State Thevenins theorem.

Ans: Any linear active network with output terminals A, B as shown in fig. (a) can be replaced by a single voltage source (V_Th = V_oc) in series with a single impedance (Z_Th = Z_i). Job at

V_Th  is the Thevenin's voltage. It is the voltage between the terminals A and B on open circuit condition. Hence it is called open circuit voltage and is denoted by V_oc

 

122. State Tellegen's theorem.

Ans: "In any network the summation of instantaneous powers or the summation of complex powers of sinusoidal sources is zero. The network may be linear, non-linear, passive or active and time invariant or varying."

For instantaneous power the theorem may be expressed mathematically as

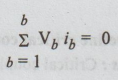 where b is the number of branches in the network.

 

123. State reciprocity theorem.

Ans: In a linear, bilateral network a voltage source V volts in a branch gives rise to a current I in V another branch. If V is applied in the second branch the current in the first branch will be I. This V/I is called transfer impedance or resistance.

 

124. State the substitution theorem.

Ans: "Any branch of network can be replaced by a different branch, as long as its potential and current remain unchanged. When the original branch is passive, either a voltage source or a current source is usually used for the substituted branch."

125. State Norton's theorem.

Ans:

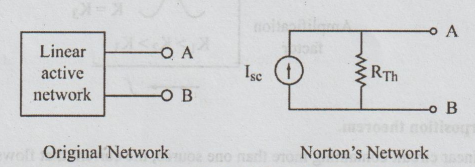
"Any linear active network with output terminals A, B as shown in the figure can be replaced by a single current source. I_SC (I_N) in parallel with a single impedance Z_Th (Z_n)  = R_Th ( = R_N)"

I_SC is the current through the terminals AB of the active network when shorted. Z_Th is the Thevenin's impedance.