Types of stresses and strains

TYPES OF STRESSES AND STRAINS

The basic types of stress and strain are given below:

1. Tensile Stress and Tensile Strain

2. Compressive Stress and Compressive Strain

3. Shear Stress and Shear Strain

4. Bending Stress and Bending Strain

 

1. TENSILE STRESS AND TENSILE STRAIN

Tensile Stress (f_t)

Fig. 1(i) shows a bar subjected to the action of a pulling load P along the axis. The load P tends to pull apart the particles of the bar and to increase the length of the bar in the direction of application of the load.

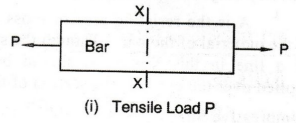
Pulling load P is called Tensile Load or Tensile Force. The corresponding stress is called Tensile Stress.

Fig. 1(ii) shows the resisting forces R at section XX. Assuming the bar to be in equilibrium, the resisting force R = pulling load P.

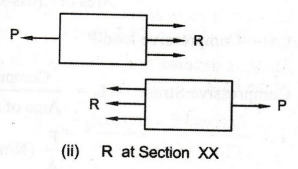
Fig. 1(iii) shows a cross-sectional element of the bar subjected to tensile stress f_t.

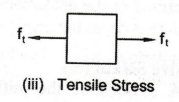
A is the resisting area or cross-sectional area of the bar. Though the stress is shown by a line in this Figure, it should be assumed as applied over the entire cross-section of the bar.

Tensile Stress = f_t = Resisting Force / Area of Cross-section = R / A

But, R = Tensile load P

Tensile Stress = ft = Tensile Load / Area of Cross-section

= P / A (N/m²)

Tensile Strain (et)

See Fig. 2. Let I be the initial length of the bar before the application of tensile load. After the application of tensile load P, the bar elongates or extends by an elementary length = dl.

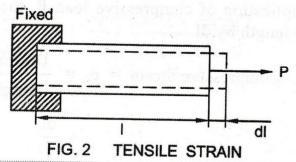
Tensile Strain = et = Increase in length / Original length = dl / l

 

2. COMPRESSIVE STRESS AND COMPRESSIVE STRAIN

Compressive Stress (f_c)

Fig. 3(i) shows a bar acted upon by an axial load P that tries to compress the bar. The load P compresses the particles of the material of the bar and decreases the length of the bar in the direction of application of the load. The load P is called Compressive Load or Compressive Force. The corresponding stress is called Compressive Stress.

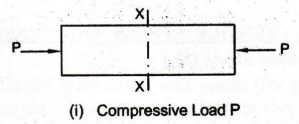
Fig. 3(ii) shows the resisting forces R at section XX. Assuming the body to be in equilibrium, the resisting force R= compressive load P.

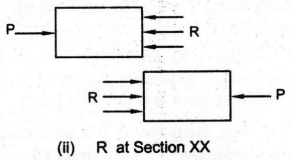
Fig. 3(iii) shows a cross-sectional element of the body subjected to compressive stress fc.

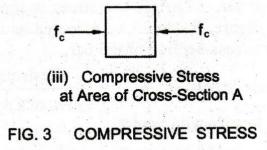
A is the resisting area or cross sectional area of the material of the bar. Though the stress is shown by a line in this Figure, it should be assumed as applied over the entire cross-section of the bar.

Compressive Stress = fc

Resisting Force / Area of Cross-section = R / A

But, R = Compressive load P

Compressive Stress = fc = Compressive Load / Area of Cross-section

= P / A (N/m²)

 

Compressive Strain (ec)

See Fig. 4. Let l be the initial length of the bar before the application of compressive load. After the application of compressive load P, the bar decreases in length by dl.

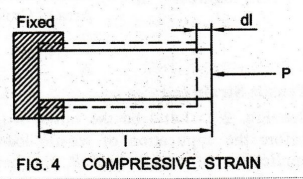
Compressive Strain = ec = Decrease in length / Original length

= dl / 1

 

3. SHEAR STRESS AND SHEAR STRAIN

Shear Stress (q)

See Fig. 5(A). It shows a riveted joint subjected to the action of two equal and opposite forces P. P acts tangentially to the resisting section XX, causing sliding of the particles one over the other.

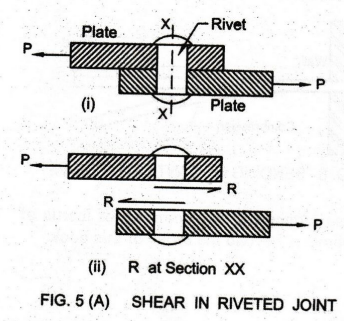
Section XX of the rivet holds the plates together and resists the tendency of the plates to get sheared-off (torn-off). In this example, the rivet section is said to develop shear stress.

See Fig. 5(B). Consider a square block ABCD of length 1, height h and width of 1 unit. The bottom face AB is fixed. A force P is applied tangentially along the top face DC.

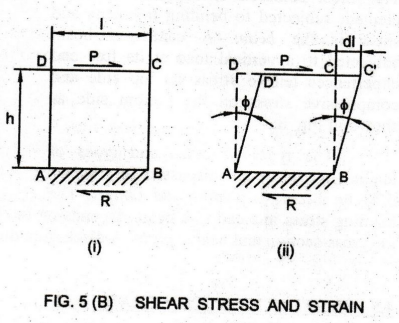
To keep the block in equilibrium, the fixed surface at the bottom will offer an equal and opposite reaction R towards left as shown. Therefore, the block is made to slide sideward to the new position D'C' as shown in Fig. 5 (B). The applied transverse load P is called the Shear Force.

Shear Force P tends the upper part of the block to slide towards right along any of the horizontal planes considered in the block. But, the block offers an internal resistance against the sliding. This internal resistance is called Shear Resistance. This shear resistance per unit crosssectional area is called Shear Stress q.

Shear Force Shear Stress = q = Shear Force / Area of Cross-section = P/ A (N/m²)

Shear Strain (es)

See Fig. 5(B). The top of the block is distorted by an amount di due to the shear force. Let the angle of distortion be φ. as shown. The intensity of this angular deformation is proportional to the distance of the fiber from the fixed base.

Shear Strain is defined as the ratio of the transverse (horizontal) displacement to the distance from the fixed lower base. It is denoted as es.

Shear Strain = es = Transverse Displacement / Distance from the fixed Base = dl / h = tan φ

In this equation, φ is the angle in radian through which the block is distorted by the shear force. The shear deformation is so small that there will be no error in approximating tan φ as φ.

Shear Strain = e = tan φ = φ, where φ is the angle of distortion in radians.

 

4. BENDING STRESS AND BENDING STRAIN

The most common or simplest structural element subjected to bending moments and shear is the beam. A cantilever beam subjected to a vertical load at its free end experiences tensile stress on top side and compressive stress on the bottom side as shown in Fig. 6.

The types of beam and types of loading on beam are discussed in Chapter on Beams, Columns and Lintels. The bending stress induced in a beam depends on the bending moment, area of moment of inertia of the cross-section and beam height. A discussion on the above is beyond the scope of this book.

 

5. OTHER TYPES OF STRAIN

Longitudinal Strain or Linear Strain: The deformation of a body in the direction of force per unit original longitudinal dimension is called the Longitudinal Strain or Linear Strain.

Longitudinal Strain =  Change in Length in the direction of Force / Original Length

Lateral Strain: When an elastic body is subjected to an axial stress, within the Elastic Limit (discussed later), it deforms not only in the direction of stress but also in the lateral direction. The lateral deformation per unit original lateral dimension is called the Lateral Strain. But the lateral strain is opposite in nature to the longitudinal strain.

For example, under the action of an axial tension, the length of the body increases. But, its breadth and thickness decrease. Under axial compression, the length decreases but the lateral dimensions, breadth and thickness, increase.

Lateral Strain = Increase / Decrease in Lateral Dimension  / Original Lateral Dimension

Volumetric Strain: It is the ratio of change in volume to original volume of an object.

Volumetric Strain = Change in Volume / Original Volume = dv /