Worked examples: AC circuit

WORKED EXAMPLES

Example 4 A voltage v = 100 sin 100 nt is applied to a circuit consisting of a pure resistor of 20 Ω Find the following quantities.

(a) Maximum voltage

(b) Frequency of supply

(c) The expression for the instantaneous current

Solution: Data:

v = 100 sin 100 πt … (i)

R = 20 Ω

The standard form of sinusoidal voltage is given by v = Vm sin ot

Comparing equations (i) and (ii)

V_m = 100 volts

ω = 100 π

⇒ 2 π f = 100 π

⇒ f 100π / 2π = 50 Hz

The expression for the instantaneous current is

 i = v / R

= 100 / 20 sin 100πt

i = 5 sin 100лt

Example 5 An inductive coil has negligible resistance and inductance of 0.1 henry. It is connected across a 220 V, 50 Hz supply. Find the current and power. Also write down the expressions for instantaneous applied voltage and current.

Solution: Data:

L = 0.1 H

V = V_RMS = 220 V

f = 50 Hz

Required: (a) I, (b) W, (c) v, (d) i

 (b) The average power consumed by inductive

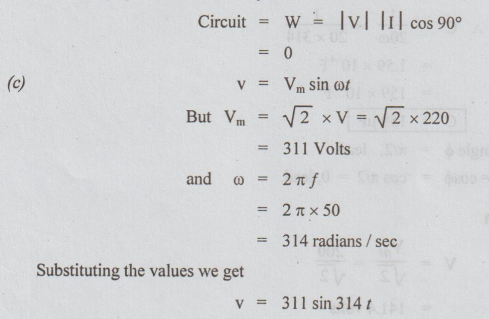
 (d) For purely inductive circuit, when V is taken as reference, i is given by

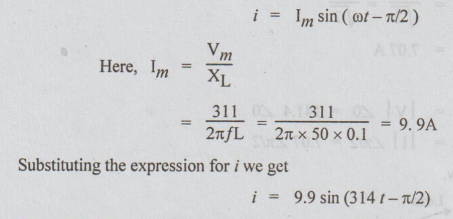
Example 6 In an A.C circuit, the applied voltage is given by v = 200 sin 314t and the expression for the leading current is given by i = 10 cos 314 t. Find the circuit constant and find the power factor of the circuit. Draw the phasor diagram.

Solution: Data:

V = 200 sin 314t ... (i)

i = 10 cos 314 t  ... (ii)

Both equations must be either in the sine form or cosine form.

The equation for i can be written as i = 10 sin (π/2 + 314 t)

= 10 sin (314t + π/2) … (iii)

Comparing equations (i) and (iii) we can say that I leads V by л/2.

i.e., the circuit element is purely capacitive.

Here V_m = 200

and I_m = 10

To draw phasor diagram

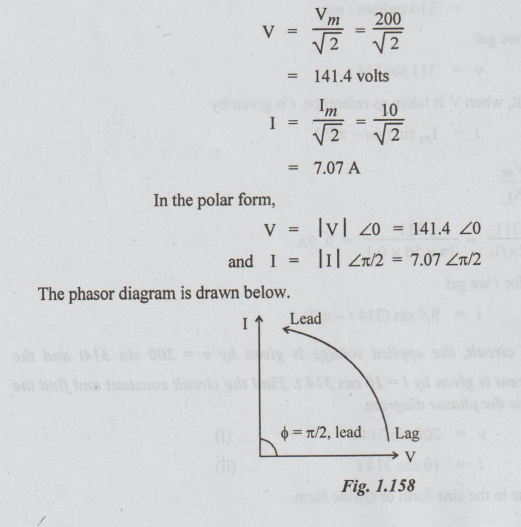
Example 7 In a circuit, the source voltage is

V = 200 sin (314t+π/6) and

the current is i = 20 sin (314t – π/3)

Find the following.

 (a) The frequency

(b) Maximum values of voltage and current

(c) RMS values of voltage and current

 (d) Average value of both voltage and current

(e) Voltage and current in polar form

(f) Draw phasor diagram

(g) Circuit element and its value.

Solution: Data:

 (g) Refer the phasor diagram. The current seems to be lagging behind the voltage by an angle = (30+ 60=90°). It is possible only when the circuit element is purely inductance.

Let the inductive reactance be X_L

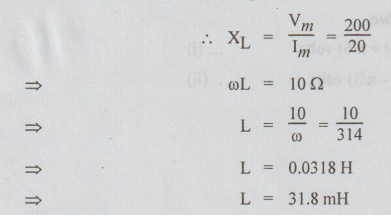
Example 8 A voltage e = 250 sin at when applied to a resistor is found to give a power of 100 watts. Find the value of resistor and write the equation for current. State whether the value of resistor varies when the frequency is changed.

Solution: Data:

The resistance is independent of frequency i.e. the variation of frequency will not affect the resistance of the resistor

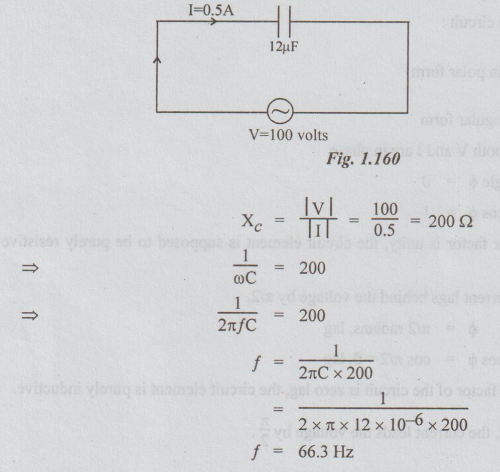
Example 9 A voltage of 100 volts is applied to a capacitor of 12uF. The current is 0.5A. What must be the frequency of supply?

Solution: Data: The given voltage and current are considered to be r.m.s. values.

i.e., V = 100 volts

I = 0.5 A

C = 12μF 12 × 10^-6F