Electric Circuit Analysis: Unit IV: Three phase circuits
Worked examples
Balanced star, delta connected load | Three phase circuits
Electric Circuit Analysis: Unit IV: Three phase circuits : Worked examples
WORKED EXAMPLES
Case
(a): Balanced star connected loads
Example
1 A balanced star connected load of (8+ j6) phase is connected to a 3 phase,
230V, 50c/s supply. Find the line current, power factor, power, reactive volt
amperes and total volt amperes.
Solution:

Example
2 A balanced star connected load of (3 - j4)2 impedance is connected to 400 V
three phase supply. What is the real power consumed?
Solution:
Note: For Star system, unless specified, the given voltage is taken as line
voltage.

Case
(b): Balanced Delta Connected Load: wel 'mdo ve
Example
3 A synimetrical 3 phase, 400 V system supplies a balanced mesh connected load.
The current in each branch circuit is 20A and the phase angle is 40° lag. Find
(a) the line current (b) the total power.
Solution:
Data: Type of connection = delta
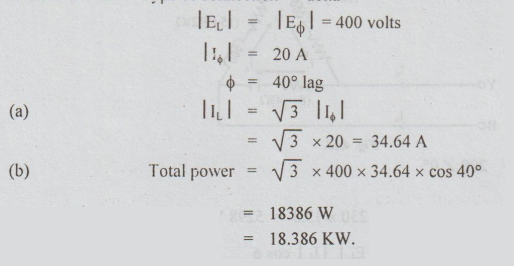
Example
4 Three impedances each of 10 resistance and 52 inductive reactance are
connected in delta to a 400 V, 36 supply. Determine the current in each phase
and in each line. Calculate also the total power drawn from the supply and the
p.f of the load.
Solution:
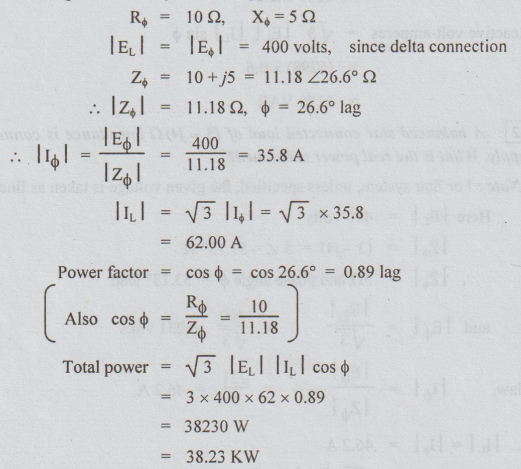
Case
(c): 3-phase unbalanced delta load fed by 3 phase balanced supply.
(i)
In this case, for a given phase sequence, the phase voltages are expressed in
polar form.
(ii)
Load impedance in each phase is expressed in polar form.
(iii)
The phase current is obtained by ohm's law. The line currents are calculated by
applying Kirchoff's current law.
Example
5 Determine the line currents for the unbalanced delta connected load of figure
given. Assume the phase sequence to be RYB. E = 200 volts.
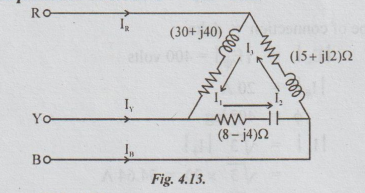
Solution :
ERY = 200 ∠ 0o
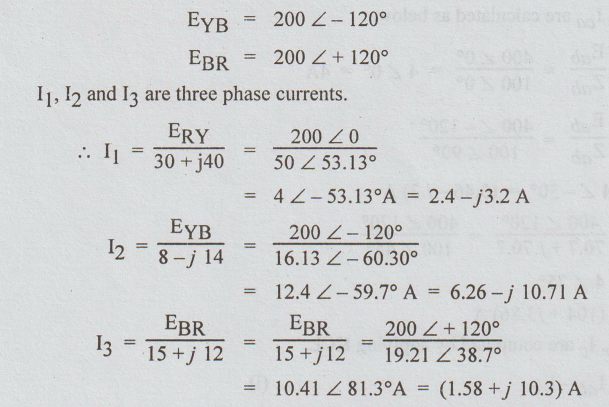
IR,
IY and IB are the line currents as shown in the circuit
diagram.
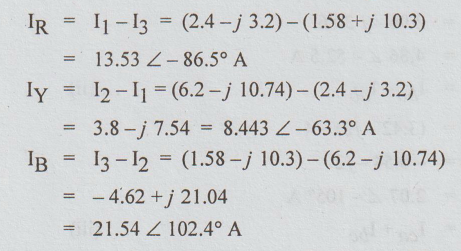
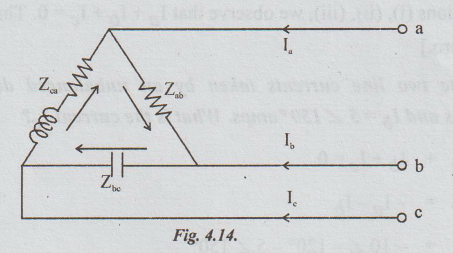
Example
6 A three phase delta connected loud has Zab= (100+ j0) olms. Zbc
= (-j100) and Zca = (70.7+j70.7) ohms and is connected to a balanced
3 phase 400V supply. Determine the line currents Ia, Ib
and I Assume the phase sequence as abc.
Solution:
For
a phase sequence abc
Eab
= 400 ∠
0°V
Ebc
= 400 ∠
-120°V, and
Eca
400 ∠ 120°V
The
phase currents lab, Ibc, Ica are calculated as below.

Now,
the line currents Ia, Ib, Ic are computed by applying KCL.
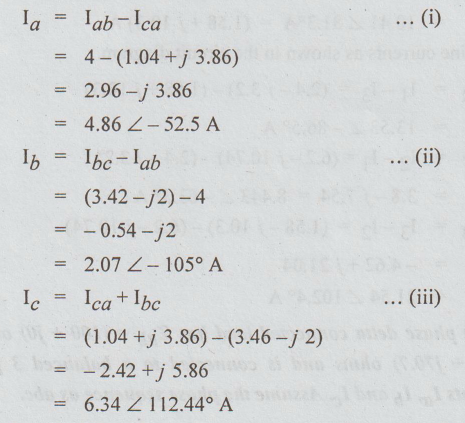
[Note: From equations (i), (ii),
(iii), we observe that Ia+Ib+ Ic=0. That is the phasor sum of the three line
currents is zero.]
Example
7 The two line currents taken by an unbalanced delta connected load are Ia =
10-120° amps and I = 5/150° amps. What is the current IC?
Solution:
Ia
+ Ib+ Ic = 0
Ic
= - Ia – Ib
=
-10 - 120°- 5150°
=
10 ∠ 60° - 5 ∠ 150°
=
(5 + j8.66) - (-4.33 + j 2.5)
=
9.33 + j 6.16
=
11.18 ∠ + 33.4° Amps
Example
8 A delta load with ZAB = 10 ∠
30° Ω, ZBC=25 20° and ZCA =
20 ∠
-30° is connected to a 3 phase 500 volt. ABC system. Find the line currents and
total power.
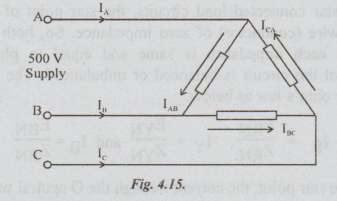
Solution:
Let the phase sequence be ABC..
Let
EAB = 500 ∠
0°
volts, EBC = 500 ∠ -120°
and ECA = 500 ∠ 120°.
To
calculate the phase currents IAB IBC and ICA:

The
line currents IA, IB and IC are calculated as below by applying KCL.

Total
power = Power in ZAB + Power in ZBC + Power in ZCA
=
(500 × 50 cos 30°) + (500 × 20) cos 0° + 500 × 25 cos 30°
=
42476 W = 42.476 KW
[To
check: Total power = sum of powers dissipated in the resistance parts
of the impedances
=
502 × 8.66 + 202 (25) + 252 (17.32) = 42476 W]
Case
(d): Unbalanced-Star connected load fed by 3 phase balanced supply.
(i) 4 wire star connected unbalanced load:
(When load star point is connected to source neutral)
In
a 3 phase, 3 wire star connected load circuits, the star point of load and
generator are tied together through neutral wire (conductor) of zero impedance.
So, both star points are at the same potential. Voltage across each impedance
is same and equal to phase voltage of the source, irrespective of the fact that
the circuit is balanced or unbalanced. The three phase currents or line
currents are determined by ohm's law as below.
IR
= ERN / IRN, IY = EYN / ZYN and
IB = EBN / ZBN
By
applying KCL at the star point, the current through the O neutral wire is given
by
IN
+ IR + IY + IB = 0
⇒ IN = (IR
+ IY + IB)
If
this load is balanced IN = 0, hence the neutral wire is omitted.
[Note:
If the neutral wire is disconnected in a 3 phase 4 wire unbalanced star load,
the potential difference across high resistance is increased and that across
low resistance is decreased.]
(ii)
Unbalanced star connected load: (without neutral):
When
a star connected load is unbalanced, having no neutral wire, then its star
point is isolated from the star point of generator. The potential of the load
star point is different from that of generator star point. The potential of the
former is subjected to variations according to the imbalance of the load. This
isolated load star point or neutral point is called a floating neutral point,
because its potential is always changing and is not fixed.
Such
unbalanced star connected loads having isolated neutral points can be analysed
by the following four method:
(a)
Star - delta conversion
(b)
Application of Kirchoff's laws
(c)
By Millmans theorem
(d)
Loop analysis or Nodal analysis
Example
9 A 3-phase, 4 wire, 208 V, ABC system supplies a star connected load in which
ZA = 10 ∠
10°Ω ZB = 15 ∠ -30°
Ω Find the line currents, the neutral currents and the load power.
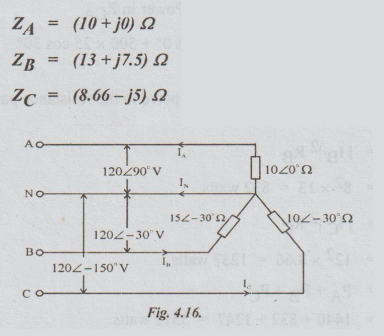
Solution:
Let us assume that the phase sequence be positive i.e., ABC, let the angle of
voltage EAN be taken at angle of 90°.
[Note:
We can take EAN as at angle 0 also.]
As
the supply system is 4-wire, it will have neutral point. The star point of the
load system is shown. It is assumed to be connected to neutral point of the
supply. Hence, the load phase voltage is same as supply phase voltage. So, we
can calculate the currents IA, IB, IC and IN as shown below: The given voltage
208 volts is the line voltage.

This
current is in the direction shown.
Calculation
of powers in the load:
Powers
are calculated using the formula, power = P = I2R
Power
in load ZA = | IA |2 RA

Example
10 An unbalanced star connected load shown in the fig. 4.17 is supplied from a
3 phase to the 440 volts symmetrical system. Determine the line currents and
the power input to the circuit.
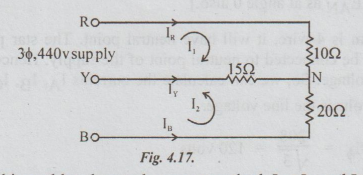
Solution:
Let us solve this problem by mesh current method. Let I1 and I2 be the loop
currents as shown. Assume the phase sequence to be RYB. Taking ERN as
reference, we can express the various voltages as below:

Example
11 A star connected load with neutral isolated, has impedances of ZA
= 15 = Ω ; ZB = 10 ∠
30° Ω ; and Zc =15 ∠
0° Ω. The supply voltage is 230V, ABC
system. Taking EBC as reference, determine the line currents and the
voltage across the load impedances.
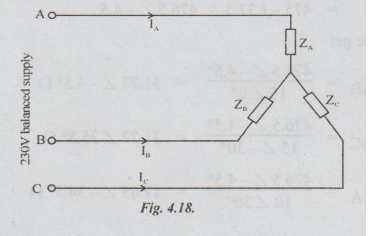
Solution:
Given
that EBC is the reference. So, the various supply voltages are shown in the
polar form as below.
EBC
= 230 ∠ °V
ECA
= 230 ∠ -120°V
and
EAB = 230 ∠
120° V
As
the neutral is isolated, the load phase voltage is not equal to supply phase
voltage. Hence, this type of problem can be solved by many ways like loop
current method, Star Delta conversion method, Kirchoff's laws methods and
application of Milliman's theorem. Let us apply here Star-Delta conversion
method.
Let
ZAB, ZBC, ZCA be the impedances of equivalent
Delta.

Now,
refer the following fig. 4.19,
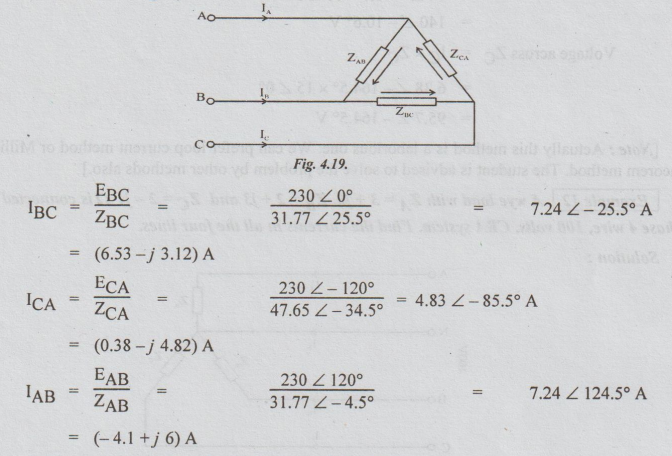
Now,
the line currents are found as below by applying KCL :

These
line currents will be the currents flowing in the given circuit also. i.e.,
star connection given.
To
determine the voltages across the load impedances:
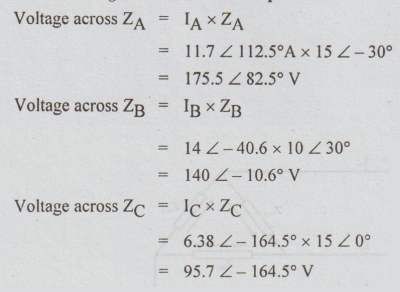
[Note: Actually this method is a
laborious one. We can prefer loop current method or Milliman's theorem method.
The student is advised to solve the problem by other methods also.]
Example
12 A wye load with ZA = 3 + j0, ZB = 2 + j3 and ZC
= 2 - j1 Ω is connected to a 3 phase 4 wire, 100 volts, CBA system. Find the
currents in all the four lines.
Solution:

As
the star point of load is connected to neutral point of supply, potential
between supply neutral point and load star point is zero. [Assuming that the
impedance of neutral wire is zero.]
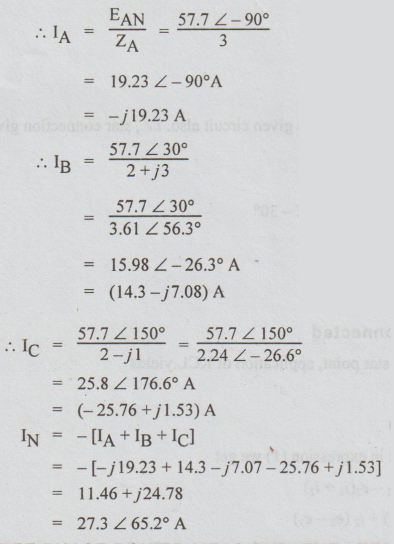
Electric Circuit Analysis: Unit IV: Three phase circuits : Tag: : Balanced star, delta connected load | Three phase circuits - Worked examples
Related Topics
Related Subjects
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
