x2-test to test the independence of attributes

c.  x²-test to test the independence of attributes

Let us consider two attributes A and B. A divided in r classes A₁, A₂, ... A, and B divided into S classes B₁, B₂, ... B_s. If this is expressed as r × s matrix, the matrix is called r × s contingency table.

If (A_i), (B_j) represent the number of persons possessing the attribute A_i, and B_j respectively (i 1, 2, ..., r, j = 1, 2, .... s) and (A_i B_j) represents the number of persons possessing attributes A_i and B_j.

That is, the expected frequency in each cell is

= Product of column total and row total / whole total

Note (2): If the calculated x² value <table value of x², we accept H_o, namely that the two attributes are independent.

If calculated x² > table value of x², then Hypothesis H₀ is rejected and conclude that the attributes are not independent.

Note (3): If a | b / c | d is the 2 × 2 contingency table with two attributes,

O = ad – bc / ad + bc is called the coefficient of association.

If the attributes are independent then a / b = c / d.

Note (4) : YATE's Correction: In a 2 × 2 table if the frequency of a cell is small say 3 or 4, we make Yate's correction to make x² continuous.

Correction: Calculate ad and bc, and add 0.5 to both factors of the small product and subtract 0.5 from both factors of the larger product.

Note (5) After Yate's Correction,

 

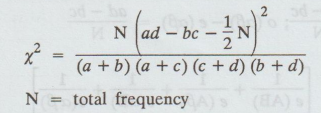
Example 1.4.c.(1)

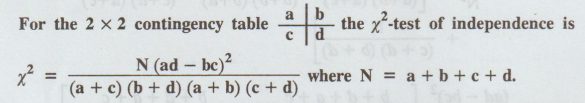
Proof: Let the two attributes be A and B. Then the 2 × 2 contingency table is given below :

 

Example 1.4.c.(2)

What are the expected frequencies of 2 × 2 contingency table 

Solution: The contingency table is [A.U A/M 2015 R-13]

 

Example 1.4.c. (3)

Find if there is any association between extravagance in fathers and extravagance in sons from the following data.

Determine the coefficient of association also.

Solution :

 

Example 1.4.c. (4)

On the basis of information noted below, find out whether the new treatment is comparatively superior to the conventional one.

Solution :

Here É‘ =  40, b = 70, c = 60, d = 30

a + b + c + d = 200

1. H₀ : No difference between the two treatment.

2. H₁ : difference between the two treatment.

3. α = 0.05, d.f  = (r - 1) (s - 1) = (2-1) (2-1) = 1

4. Table value of x²: 3.841

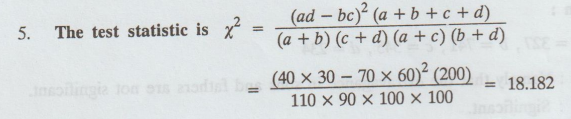
6. Conclusion :

Here, Cal x² > table x²

i.e., 18.182 > 3.841

So, we reject H₀ at 5% level of significance.

We conclude that the treatments are not independent.

 

Example 1.4.c.(5)

1000 students at college level were graded according to their I.Q. and their economic conditions. What conclusion can you draw from the following data:

Solution :

Here É‘ = 460, b = 140, c = 240, d = 160

1. H_{0 :}  The given attributes are independent.

2. H₁ : The given attributes are not independent.

3. α = 0.05, d.f = (r – 1) (s – 1) = (2 – 1 ) ( 2 – 1 ) = 1

4. Table value of x²: 3.841

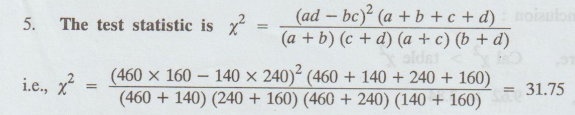
6. Conclusion :

Here, Cal x² > table x²

i.e., = 31.75 > 3.841

So, we reject Ho at 5% level of significance.

We conclude that the attributes I.Q. as Economic conditions are not independent.

 

Example 1.4.c. (6)

Out of 8000 graduates in a town 800 are females, out of 1600 graduate 0001 employees 120 are females. Use x² to determine if any distinction is made in appointment on the basis of sex. Value of x² at 5% level for one degree of freedom is 3.84. [A.U A/M 2010]

Solution: Given:

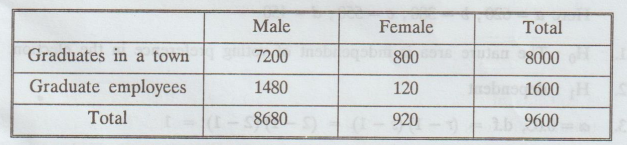
Here a = 7200, b = 800, c = 1480, d = 120

1. H₀ : There is no significant difference between male and female.

2. H₁ There is significant difference between male and female.

3. α = 0.05, d.f= (r− 1) (s - 1) = (2-1) (2 − 1) = 1

4. Table value of x²: 3.84

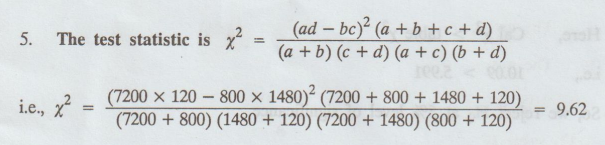
6. Conclusion:

Here, Cal x² > table x²

i.e., 9.62 > 3.840

So, we reject H₀ at 5% level of significance.

 

Example 1.4.c. (7)

Two sample polls of votes for two candidates A and B for a public office are taken one one from among res among residents of rural areas. The results are given below. Examine whether the nature of the area is related to voting preference in this election. [A.U N/D 2011]

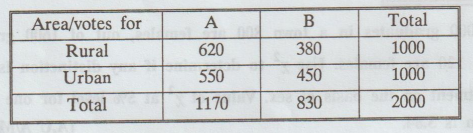
Solution :

Here a = 620, b = 380, c = 550, d = 450

1. H₀ : The nature area is independent of voting preference in the election.

2. H₁: dependent

3. α = 0.05, d.f = (r − 1) (s − 1) = (2-1) (2 − 1) = 1

4. Table value of x² : 5.991

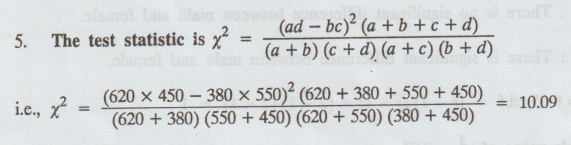
6. Conclusion :

Here, Cal x²  > table x²

i.e., 10.09 > 5.991

So, we reject Ho at 5% level of significance.

 

Example 1.4.c.(8)

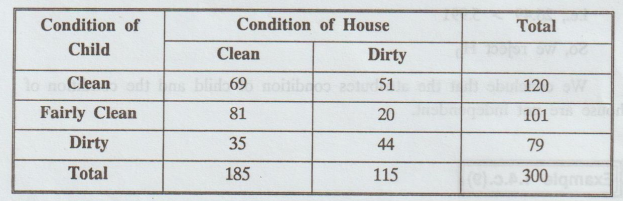
From the following information state whether the condition of the child is associated with the condition of the House.

Solution :

1. H₀ : The given attributes are independent.

2. H₁: The given attributes are not independent.

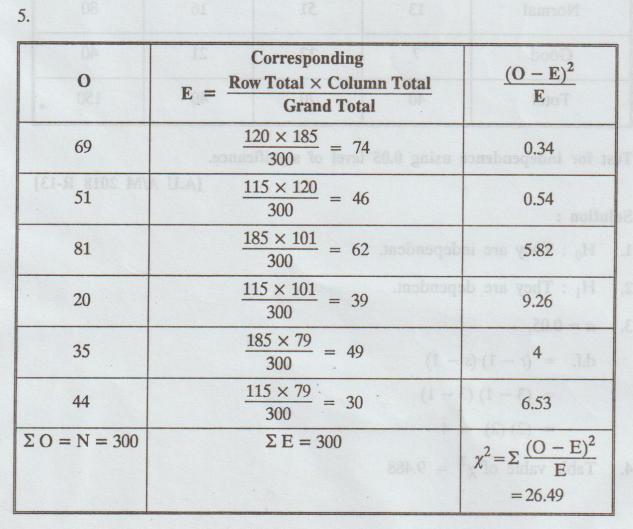
3. α = 0.05, d.f = (r-1) (s1) = (3 - 1) (2 - 1) = 2

4. Table value of x²: 5.991

Cal x² = 26.49

6. Conclusion:

Here, Cal x² > table x²

i.e., 26.49 > 5.991

So, we reject H₀

We conclude that the attributes condition of child and the condition of house are not independent.

Example 1.4.c. (9)

Mechanical engineers testing a new era welding technique, classified welds both with respect to appearance and an X-ray inspection.

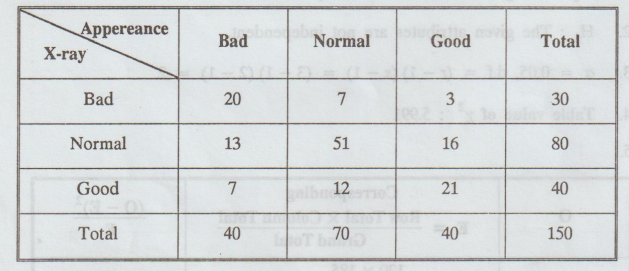
Test for independence using 0.05 level of significance. [A.U A/M 2018 R-13]

Solution :

1. H₀ : They are independent.

2. H₁ : They are dependent.

3. α = 0.05,

d.f. = (r − 1) (s - 1)

= (3-1) (3-1)

= (2) (2) = 4

4.  Table value of x² = 9.488

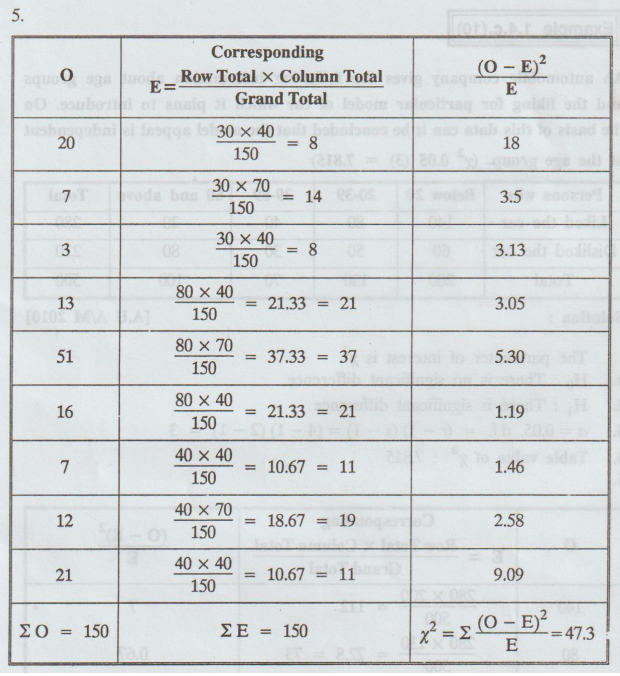
Converting E_i's into whole number such that ΣE = ΣO

6. Conclusion:

Cal x² > table x²

47.86 > 9.488, So we reject the null hypothesis.

X-ray and Appearance are dependent.

 

Example 1.4.c.(10)

An automobile company gives the following information about age groups and the liking for particular model of car which it plans to introduce. On the basis of this data can it be concluded that the model appeal is independent of the age group. (x².05 (3) = 7.815) [A.U A/M 2010]

Solution :

The parameter of interest is x²

1. H₀ There is no significant difference

2. H₁ There is significant difference

3. ɑ = 0.05, d.f. = (r-1) (s-1) = (41) (2 − 1) = 3

4. Table value of x² : 7.815

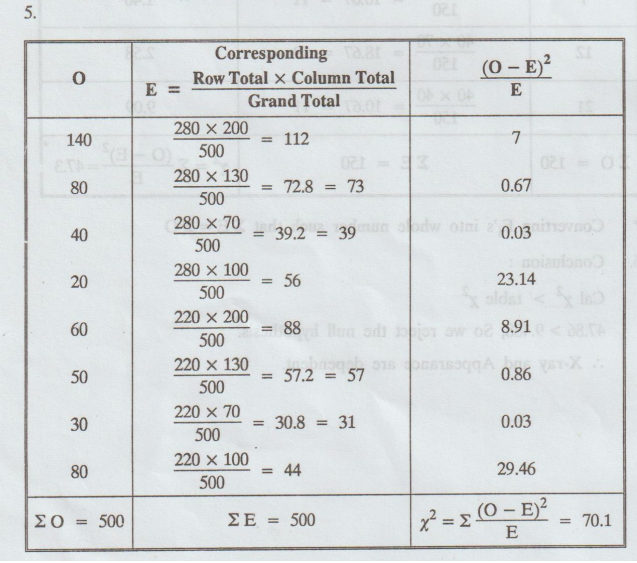
Converting E_i's into whole number such that ΣE = Σ O

6. Conclusion:

Here Cal x² > table x²

i.e., 70.1 > 7.815

So, we reject H₀ at 5% level of significance.

 

Example 1.4.c. (11)

Using the data given in the following table to test at 1% level of significance whether a person's ability in Mathematics is independent of his/her interest in Statistics. [A.U N/D 2017 R-13]

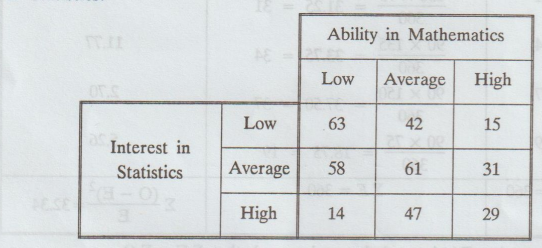
Solution:

The parameter of interest is x²

1. H₀ : Ability in mathematics and interest in statistics are independent

2. H₁ : Ability in mathematics and interest in statistics are not independent

3. a = 0.01,

d.f = (r - 1) (s - 1)

= (3-1) (3-1)

= 4

4. Table value of x² = 13.277

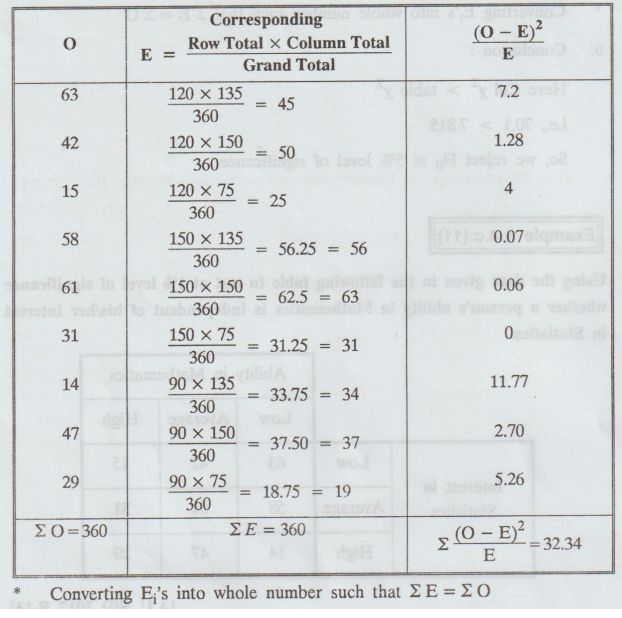
6. Conclusion :

Here, Cal x² > table x²

i.e., 32.34 > 13.277

So, we reject H₀ at 1% level of significance. 

 

EXERCISES 1.4(c).

1. The chi-square value of 2 × 2 table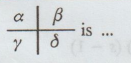 

2. If A, B are two independent attributes and if (A) = 36 (B) = 25 and N = 100 find (AB).

 [Hint. (AB) = (A) / N = (B) 36 × 25 / 100 = 9]

3. 200 digits were chosen at random from a set of table. The frequencies of the digits are:

Use x² test to assess the correctness of the hypothesis that the digits were distributed in equal numbers in the tables from which these numbers were taken. 200

[Ans. x² = 4.3 Ho is accepted]

4. The theory predicts the proportion of beans, in the four groups bas G1, G2, G3, G4 should be in the ratio 9: 33: 1. In an experiment, with 1600 beans the numbers in the four groups were 882, 313, 287 and 118. Does the experimental result support the theory.

 [Ans. Supports the theory x² = 4.7266]

5. A die is thrown 276 times and the results of these throws are given below :

Test whether the die is biased or not.

6. A die is thrown 264 times and the results are given below :

Show that the die is biased.

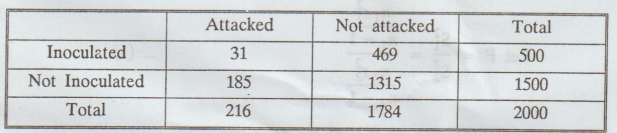
7. The table given below shows the data obtained during an epidemic of cholera. Test the effectiveness of inoculation in preventing the attack of cholera.

8. In a certain sample of 2000 families 1400 people are consumers of tea. Out of 1800 Hindu families 1236 families consume tea. Use x2-test and state whether there is any significant difference in consumption of tea among Hindu and Non-Hindu families.

9. From the data given below compare the association between literacy and unemployment among males using x² - test. Total 250; Literate 100; Unemployed 50; Literate and unemployed 30.