Anna university solved problems

ANNA UNIVERSITY SOLVED PROBLEMS

Problem 1.1

A parallel plate capacitor consists of two plates each of area 5 × 10^-4 m². They are They are separated by a distance 1.5 x 10^-3 m² and filled with a dielectric of relative permittivity 6. Calculate the charge on the capacitor if it is connected to a 100 volt DC supply. (A.U. Dec 2012)

Given data

Area of the capacitor plate A = 5 × 10^-4 m²

Distance between the plates d = 1.5 x 10^-3 m

Relative permittivity of the dielectric ε_r = 6

Applied voltage V = 100 V

Permittivity in free space, ε₀ = 8.85 × 10^-12 Fm ^-1

Solution:

We know that Q = CV

Also, we have the relation

 C = ε₀ ε_r A / d

Q = ε₀ ε_r A V / d

Substituting the given values, we have

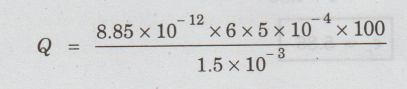
Q = 1.77 × 10^-9 C

Charge on the capacitor = 1. 77 × 10^-9 Coulomb.

Problem 1.2

If a NaCl crystal is subjected to an electrical field of 1000 V/m and the resulting polarisation is 4.3 × 10^-8  C/m², calculate the relative permittivity of NaCl.  (A.U. April 2012)

Given data

Applied electrical field E = 1000 V m^-1

Polarisation P = 4.3 x 10^-8 Cm ^-2

permittivity ofPermittivity in free space ε₀ = 8.85 x 10^-12 Fm^-1

Solution:

We know that  P = ε₀ (ε_r -1) E

(ε_r -1) = p / ε₀ Ε

ε_r = 1+ p / ε₀ Ε

Substituting the given values we have

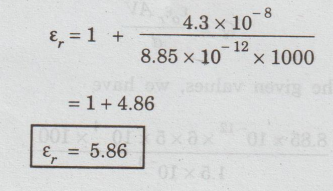
= 1+ 4.86

ε_r  = 5.86

Problem 1.3

Calculate the electronic polarisability of argon atom given ε_r = 1.0024 at NTP and N=2.7 x 10²⁵ atoms/m³.  (A.U. Nov 2011)

Given data

Relative permittivity ε_r = 1.0024

Number of atoms per unit volume N = 2.7 × 10²⁵ atoms m^-3

Permittivity in free space ε₀ = 8.85 x 10^-12 F m^-1

Solution:

We know that P = ε₀ (ε_r -1) E

Also, P = Nα_e E

Nα_e E = ε₀ (ε_r -1) E

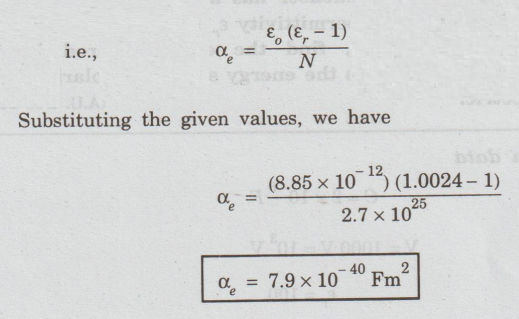
Problem 1.4

The dielectric constant of He gas at NTP is 1.0000684. Calculate the electronic polarisability of He atoms if the gas contains 2.7 x 10²⁵ atoms per m³  (A.U. Nov 2014)

Given data

Dielectric constant of the gas at NTP ε_r = 1.0000684

Number of He atoms per unit volume N = 2.7 × 10²⁵ m³.

Solution

Electronic polarisability is given by

α_e = ε₀ (ε_r-1) N / N

Substituting the given values, we have

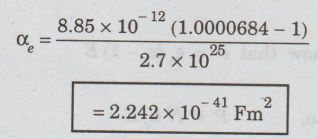
Problem 1.5

A parallel plate condenser has a capacitance of 2 μ F. The dielectric has permittivity ε_r = 100. For an applied voltage of 1000 V, find the energy stored in the condenser as well as the energy stored in polarising the dielectric. (A.U. Dec 2016)

Given data

C = 2 × 10^-6

V = 1000 V = 10³ V

ε_r = 100

Solution:

Total energy stored in the capacitor E = ½ CV²

E = ½ × 2 × 10^-6 × (10³)² = 1J

To calculate the energy stored in the dielectric material which is in between the parallel plates of the condenser, capacitance has to be calculated by removing the dielectric material.

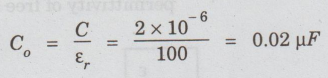
Energy stored without the dielectric,

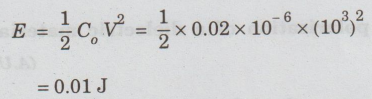
Hence, energy stored in the dielectric

E' =E-E₀=1-0.01

E' = 0.99 J